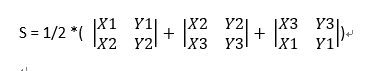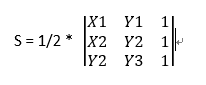突然感兴趣就想写一下:
已知:平面内三点坐标(X1,Y1),(X2,Y2),(X3,Y3)
问题:求由这三点所围成的三角形的面积(三点各不相同)
分析:
第一种:
(注意:在坐标系中顺序为三点按逆时针排列)
第二种:
总的来说公式就是:
S=1/2 * [(x1y2-x2y1)+(x2y3-x3y2)+(x3y1-x1y3)]
下面给出C++的一个函数代码
double gets(vector<int>p1, vector<int>p2, vector<int>p3){
return 0.5 * ((p1[0]*p2[1] - p2[0]*p1[1]) + (p2[0]*p3[1] - p3[0]*p2[1]) + (p3[0]*p1[1] - p1[0]*p3[1]));
}
今天的文章已知三点坐标,求围成的三角形面积的一个公式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/4943.html