零极点概念总结

转折频率：即AF对数坐标轴的转折线，高频部分的渐近线是一条斜率为－20dB/dec的直线，当输入信号的频率每增加十倍频程时，对应输出信号的幅值便下降20dB。
截止频率：用来说明电路频率特性指标的特殊频率。当保持电路输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，用频响特性来表述即为-3dB点处即为截止频率。
或某一特殊额定值时该频率称为截止频率。其实就是转折频率。转折频率=截止频率
剪切频率：在开环对数频率特性上对应于幅值A（w）=1(即20lg|A(w)|=0）的角频率称为剪切频率，通常以Wc表示。
穿越频率：用来描述系统频率特性的一个指标，也称剪切频率。其定义为幅频穿越0dB处的频率，穿越频率对应的相频曲线上的相位反映了系统的相对稳定性。相位裕度定义为穿越频率对应的相位+180°，相位裕度大于0表示系统稳定，小于0系统不稳定（如下图“角频率Wc”处）。
穿越频率 == 剪切频率=fc表示；f0表示起始反馈振荡频率。
f_{0[/sub],=为相频穿越-180°时的频率,即产生自激正当的频率。}
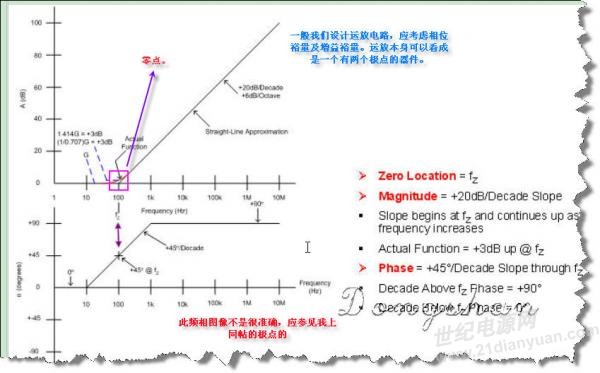
极点：转折频率所在X轴坐标对应每一次-3db下降的点；极点之后每十倍频，增益下降20db。零点与极点相反。
零点：就是使传递函数分子为零的点或者说每一段转折线的起始点。在零点之处，增益增加3db,并移相45度。零点之后，每十倍频，增益增加20db.
零状态响应：是指初始状态为零，对输入所产生的响应，类似恒压源给电容充电。

稳定裕量：是判断稳定性时，由波特图看出来的，有两种表示形式，相位裕量和幅值裕量。当相位角为180度时，所对应的响应与截至频率所对应实际响应的差值。
一、传递函数中的零点和极点的物理意义：
零点：当系统输入幅度不为零且输入频率使系统输出为零时，此输入频率值即为零点。
极点：当系统输入幅度不为零且输入频率使系统输出为无穷大（系统稳定破坏，发生振荡）时，此频率值即为极点。举例：有时你家音响或电视机壳发出一阵阵尖厉嘶嘶声，此时聪明的你定会知道机壳螺丝松了，拧紧螺丝噪声问题就解决了。其实，你所做的就是极点补偿，拧紧螺丝——你大大降低了系统极点频率。当然此处系统是指机械振动系统不是电路系统，但系统原理一样。抛砖引玉尔。希望更多答案。（这一段有待讨论）
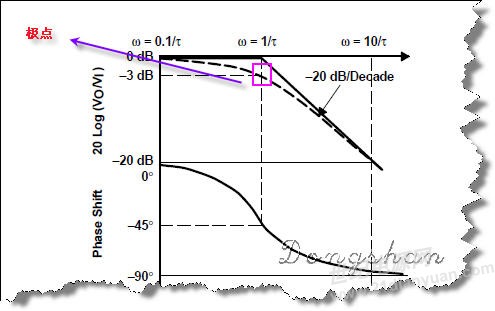
二、每一个极点之处，增益衰减-3db, 并移相-45度（可以理解成每一个转折点）。极点之后每十倍频，增益下降20db。零点与极点相反，在零点之处，增益增加3db,并移相45度。零点之后，每十倍频，增益增加20db.波德图如下：

零点图找不到合适的，不过是与极点图相反的。以下是极点图。极点零点一般用于环路的稳定性分析。

以下内容摘自某兄博客，提取扼要，增加了若干注释。
CMOS里面一般栅端到地的电容Cgs较大，所以一般人们就去取这个极点，
输入信号频率使得节点到地的阻抗无穷大（也就是所谓的1/RC）R为到的电阻，C为到地的电容（并联产生极点）
零点在CMOS中往往是由于信号通路上的电容产生的，使的信号到地的阻抗为0；
在密勒补偿中，不只是将主极点向里推，将次极点向外推（增大了电容），同时还产生了一个零点（与第三极点频率接近），只不过人们一般只关心前者。
经验上来讲，放大器电路中高阻抗的节点都要注意，即使这点上电容很小，都会产生一个很大的极点。零点一般就不那么直观了，通常如果两路out of phase的信号相交就会产生零点，但这不能解释所有的零点。
个人觉得零点、极点只是电路分析中抽象出来的辅助方法，可以通过零极点分析电路动作特征，然而既然有抽象肯定有它的物理表现，极点从波特图上看两个作用：延时（频率增加但我增益等会减少）和降低增益，在反馈系统中作用就是降低反馈信号幅度以及拖延反馈信号回到输入点的时间。所以如果某个节点存在对地电容，必然会对电容充电，同时电容和前级输出电阻还存在分压，所以这个电容会产生极点（想想采样分压电阻过来的信号，增加了一个电容滤波）。
零点可以增加增益，极点减少增益，而我们在反馈的时候，是希望在相位下降到180度之前，增益就已经降低到一，所以我们需要消除一个零点，以免发生震荡。今天的文章零极点概念总结分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。