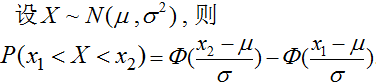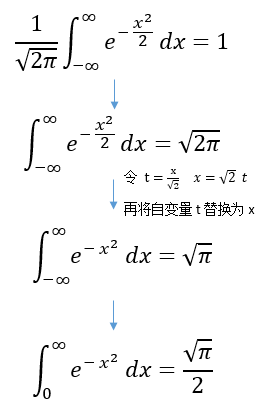1.正态分布(高斯分布)
若随机变量 $X$ 服从一个位置参数为 $\mu$ 、尺度参数为 $\sigma$ 的概率分布,且其概率密度函数为
$$ f(x) = \frac{1}{\sqrt{2\pi}\,\sigma} e^{-\frac{(x-\mu)^2}{2 {\sigma} ^2}} $$
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作 $X \thicksim N(\mu , \sigma ^2)$ 。
当$\mu = 0, \sigma = 1$时,称为标准正态分布。 $X \thicksim N(0 , 1)$
$$ f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2 }} $$
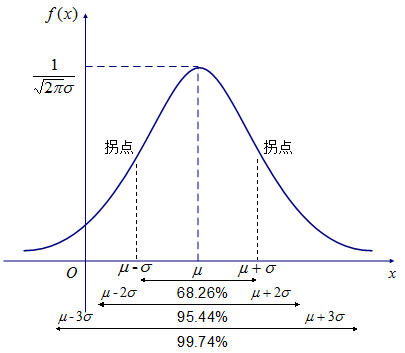
如下图是一般正态分布
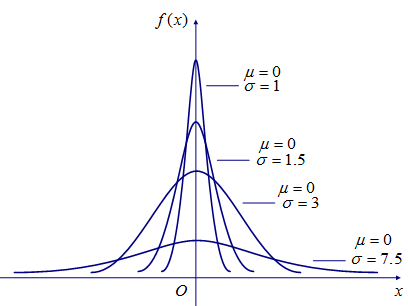
如下图是标准整体分布
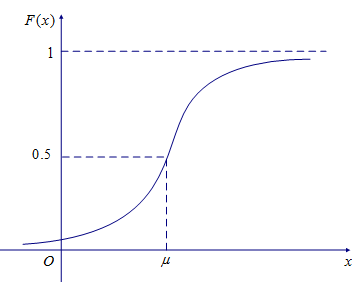
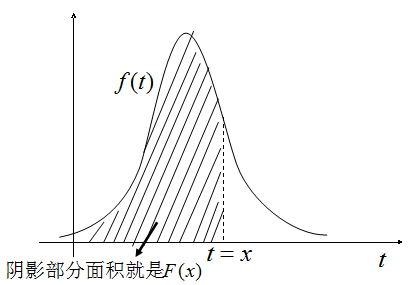
一般正态分布的分布函数$F(x)$
$$F(x)=P(X \leqslant x)= \frac{1}{\sqrt{2\pi} \sigma}\int_{-\infty}^{x}e^{-\tfrac{(t-\mu)^2}{2{\sigma}^2}}dt $$
标准正态分布的分布函数$\Phi(x)$:
$$\Phi(x)=P(X \leqslant x) = \frac{1}{\sqrt{2\pi} }\int_{-\infty}^{x}e^{-\tfrac{t^2}{2}}dt $$
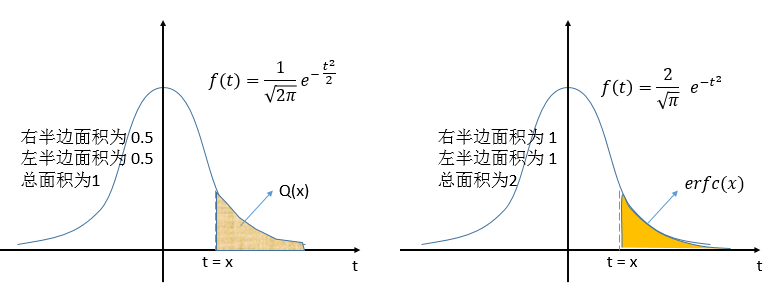
2.Q函数
Q函数又称标准正态分布的右尾函数。
$$Q(x)=\int_x^\infty\frac{1}{\sqrt{2\pi}}\ e^{-\tfrac{t^2}{2}}dt = 1-\Phi(x) $$
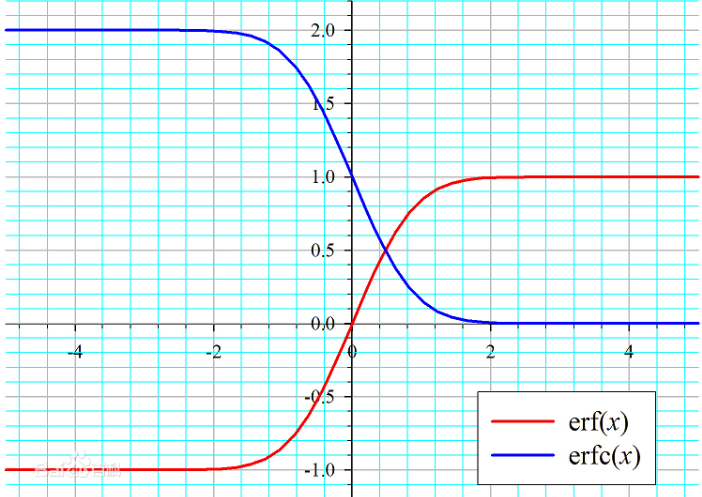
3.误差函数
$$ erf(x)=\frac{2}{\sqrt{ \pi}}\int_0^{x}e^{-t^2}dt $$
4.互补误差函数
$$ erfc(x)=\frac{2}{\sqrt{ \pi}}\int_x^{\infty}e^{-t^2}dt = 1-erf(x) $$
5.它们之间的关系
$$ Q(x) = 1-\Phi(x) $$
$$ Q(x) = \frac{1}{2} erfc(x/ \sqrt 2) $$
$$ erfc(x) = 2Q(\sqrt 2 x) $$
$$ erf(x) = 1-2Q(\sqrt 2 x) $$
$$ erf(x) + erfc(x) = 1 $$
注:
由正态分布密度函数的总积分为1(即概率 P(X<∞) = 1)得: