基于矩阵合同变换算法的无向图同构识别——C++代码实现

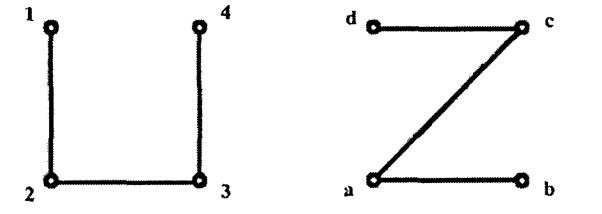
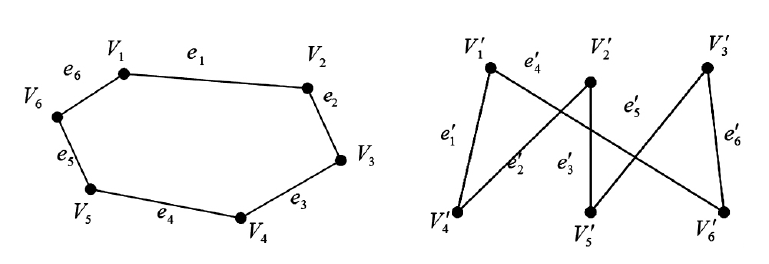
兹于2017年4月，应《算法设计与分析》课程设计的要求，本人就基于矩阵合同变换算法的图同构识别做了较为深入的理解，借助《西南民族大学学报(自然科学版)》2011年第05期，作者：谢科、饶怀章的《图同构的充要条件》，从而借助图同构的充要条件通过矩阵的合同变换来进行图同构识别，该算法对有向图和无向图均适用。

基于矩阵合同变换算法的图同构识别

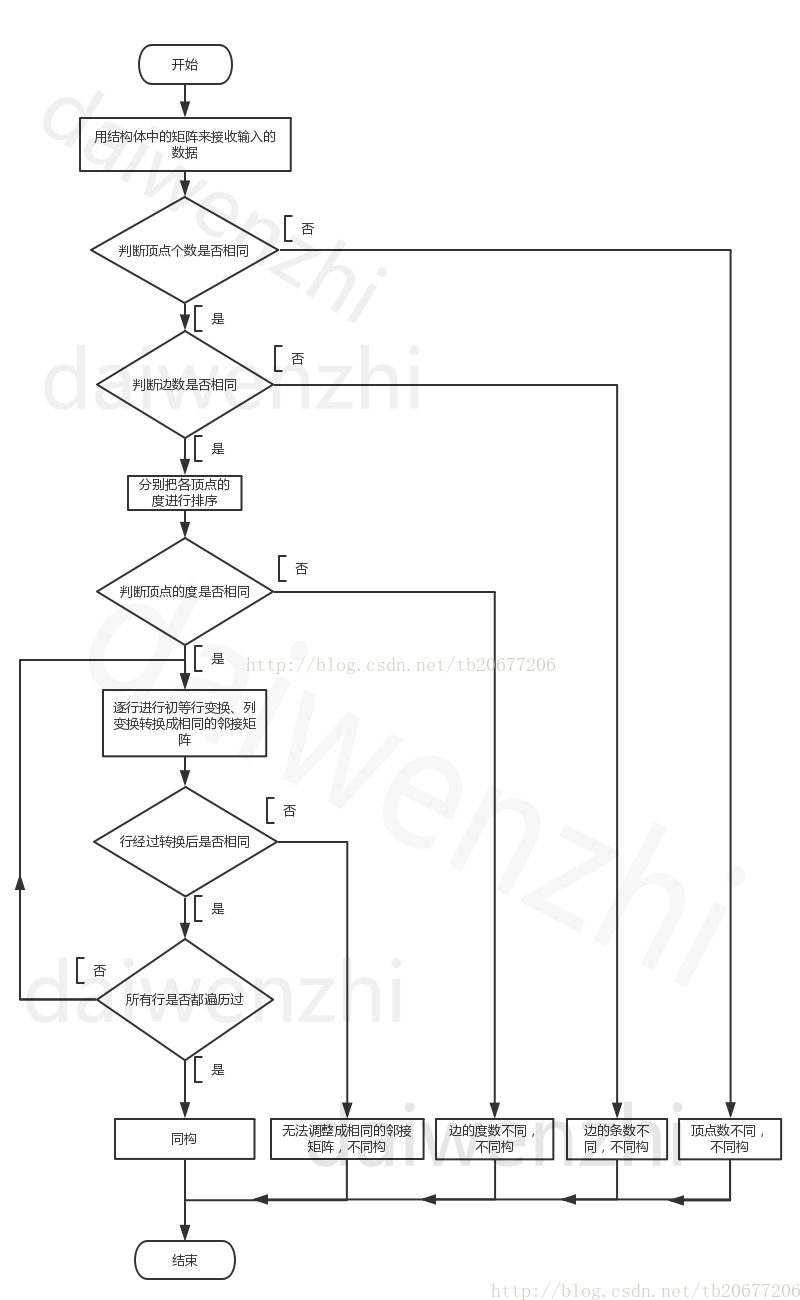
1、矩阵合同变换算法的流程图。

2、矩阵合同变换算法实现的关键代码
#include<iostream>
#include<stdlib.h>
#define MAX 100 
using namespace std;
 
 
struct AdjacencyMatrix{
    int points;             //邻接矩阵的顶点个数（即矩阵阶数）
    int edges;              //邻接矩阵的边的条数（即邻接矩阵非零点个数/2）
    int Matrix[MAX][MAX];   //矩阵
    int weight[MAX];        //行度数的集合
};
 
AdjacencyMatrix A,B;//定义邻接矩阵A、B，将A调整成B且满足同构的必要条件则A、B同构
 
 
//行位置交换函数，返回true为正常交换
bool swapRows(int i,int j){
    int k;
    //进行行交换
    for(k=0;k<A.points;k++){
        int temp;
        temp = A.Matrix[i][k];
        A.Matrix[i][k]= A.Matrix[j][k];
        A.Matrix[j][k]= temp;
    }
    int temp;
    //度交换
    temp =A.weight[i];
    A.weight[i]= A.weight[j];
    A.weight[j]= temp; 
    return true;
} 
 
 
//列位置交换函数，返回true为正常交换，false为无法交换，不同构
bool  swapColumns(intcurrentLayer,int i,intj){
    int k;
    //判断是否能交换
    for(k=0;k<currentLayer;k++){
        if(A.Matrix[k][i]!=A.Matrix[k][j]){
            //无法交换，因为交换后会影响先前调整的结果，故而不同构
            return false; 
        }
    }
    //进行列交换
    for(k=0;k<A.points;k++){
        int temp;
        temp =A.Matrix[k][i];
        A.Matrix[k][i]= A.Matrix[k][j];
        A.Matrix[k][j]= temp;
    } 
    return true;
} 
 
//用于快速排序的比较算法
int cmp( const void *a , const void *b ){ 
    return *(int *)a - *(int *)b; 
}
 
int main(){
    cout<<"请输入两个图的阶数（顶点数）："<<endl;
    cin>>A.points>>B.points;
    
    //判断第一个必要条件
    if(A.points!=B.points){
        cout<<"阶数不同！不同构！"<<endl;
        return 0;
    }
    
    cout<<"请输入第1个图的邻接矩阵："<<endl;
    A.edges = 0;
    B.edges = 0;
    
    //用邻接矩阵方式输入A、B矩阵
    int i,j,k,y;
    for(i=0;i<A.points;i++){
        for(j=0;j<A.points;j++){
            cin>>A.Matrix[i][j];
            if(A.Matrix[i][j]==1){
                A.edges++;
            }   
        }
    }
    
    cout<<"请输入第2个图的邻接矩阵："<<endl;
    for(i=0;i<B.points;i++){
        for(j=0;j<B.points;j++){
            cin>>B.Matrix[i][j];
            if(B.Matrix[i][j]==1){
                B.edges++;
            }   
        }
    }
    
    //判断第二个必要条件
    if(A.edges!=B.edges){
        cout<<"边的条数不同！不同构！"<<endl;
        return 0;   
    } 
    
    //因为是邻接矩阵，所以边的条数（即邻接矩阵非零点个数/2）
    A.edges =A.edges/2;
    B.edges =B.edges/2;
    int Aweight[MAX];
    int Bweight[MAX];
    //判断第三个必要条件
    int x=0;
    for(k=0;k<A.points;k++){
        int count=0;
        for(y=0;y<A.points;y++){
            if(A.Matrix[k][y]==1){
                count++;
            }
        }
        Aweight[x]= count;
        A.weight[x++]=count;
    } 
    qsort(Aweight,A.points,sizeof(Aweight[0]),cmp);//调用系统快速排序算法
    
    x=0;
    for(k=0;k<B.points;k++){
        int count=0;
        for(y=0;y<B.points;y++){
            if(B.Matrix[k][y]==1){
                count++;
            }
        }
        Bweight[x]= count;
        B.weight[x++]=count;
    }
    qsort(Bweight,B.points,sizeof(Bweight[0]),cmp);//调用系统快速排序算法
    
    for(k=0;k<A.points;k++){
        if(Aweight[k]!=Bweight[k]){
            cout<<"边的度数不同！不同构！"<<endl;
            return 0;
        }
    } 
    
    
    //调整A矩阵成B 
    for(i=0;i<B.points;i++){
        for(j=i;j<A.points;j++){
            //找到度相同
            if(B.weight[i] == A.weight[j]){
                //进行行交换
                if(i!=j){
                    swapRows(i,j);
                }
                
                //进行列交换
                if(i!=j){
                
                    if(swapColumns(i,i,j)==false){
                        cout<<"无法调整成相同的邻接矩阵！不同构！"<<endl;
                        return 0;
                    }       
                    
                    int list[MAX];
                    x=0;
                    //判断非零顶点所处列的位置是否相同
                    for(k=0;k<A.points;k++){//找出位置不同的点放入list 
                        if(A.Matrix[i][k]!=B.Matrix[i][k]){
                            list[x++]=k;
                        }
                    }
                    
                    for(k=0;k<x;k=k+2){
                        if(swapColumns(i,list[k],list[k+1])==false){
                            cout<<"无法调整成相同的邻接矩阵！不同构！"<<endl;
                            return 0;
                        }
                        swapRows(list[k],list[k+1]);
                    }
                }
                break; 
            } 
        }
    }
    cout<<"经过检测，两图同构！"<<endl;
    return 0;
} 
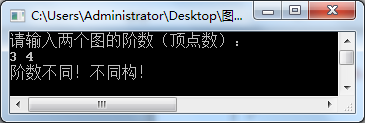
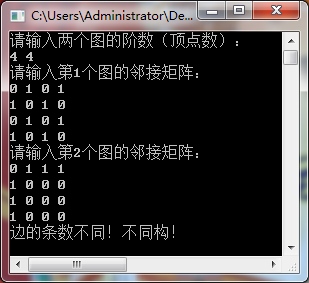
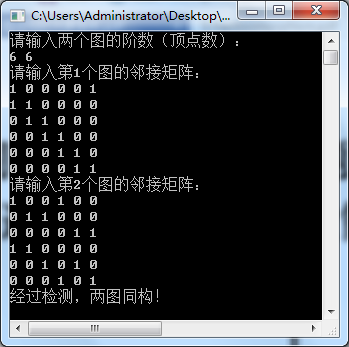
3、运行结果

阶数（顶点数）不同，不同构情况：

边的条数不同，不同构情况：

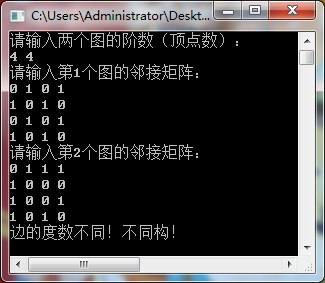
边的度数不同，不同构情况：

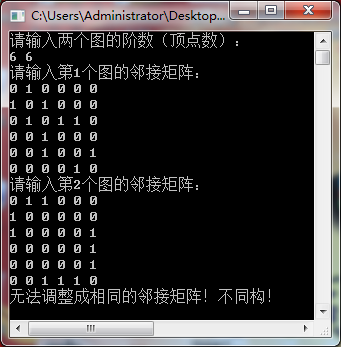
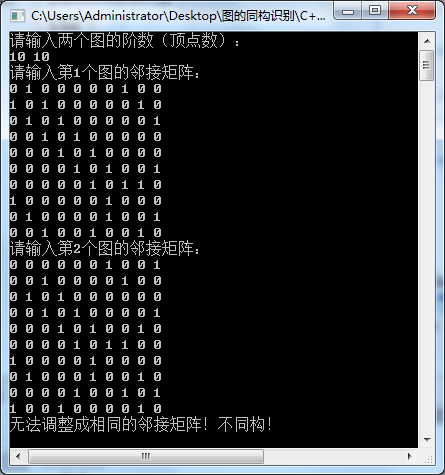
无法调整成相同的邻接矩阵，不同构情况：

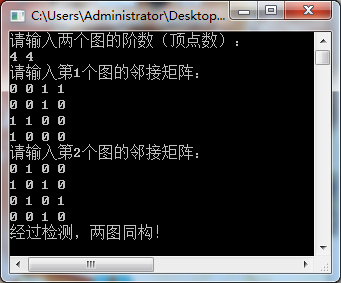
同构情况：

4、矩阵合同变换算法的计算复杂度分析（最好、最差、平均情况复杂度）

该算法主要包括了几个并列的for循环，第一个for循环是二重嵌套循环，对邻接矩阵输入初始化，时间复杂度为O(n²)，其中的n是图中的顶点数；而第二个和第三个for循环是二重嵌套循环，进行顶点的度数判别进行预处理，第四个for循环进行输出判断顶点的度数是否相同；第五个for循环使多重嵌套循环最多有4重循环，将一个邻接矩阵调整成另外一个邻接矩阵。

本算法主要是在排除非同构图方面具有较高的效率。

最好情况时间复杂度：当顶点个数不相同时，所以算法最好情况的时间复杂度为O(1)；

最坏情况时间复杂度：当两个邻接矩阵同构时，则要将所有条件都进行判断执行，所以算法最坏情况时间复杂度为O(n⁴)；

平均情况时间复杂度：假设阶数（顶点数）不同，不同构情况、边的条数不同，不同构情况、边的度数不同，不同构情况、无法调整成相同的邻接矩阵，不同构情况和同构情况，每种可能出现的概率相同为1/5，所以可得，故可得算法平均情况时间复杂度O(n⁴)。

5、总结矩阵合同变换算法

1) 首先用结构体中的矩阵来接收输入的数据

2) 然后判断是否满足两图同构的必要条件

判断顶点个数是否相同

如相同：

   判断边数是否相同

   如相同：

      再分别把各顶点的度进行排序，然后判断顶点的度是否相同

上述方法可总结出得到两图同构的必要条件：

i．结点数相等；

ii．边数相等；

iii．度数相同的结点数相等。

对照邻接矩阵，这些必要条件所反映出来的是：

i．邻接矩阵的阶数相等；

ii．矩阵中非零元的个数相等；

iii．非零元个数相等的行 (或列)数相等。

3) 最后：

如果两图能经过矩阵初等行变换、列变换转换成相同的邻接矩阵则同构

第一次发博客，写的不是很好，望各位大神多多指正，不喜勿喷。