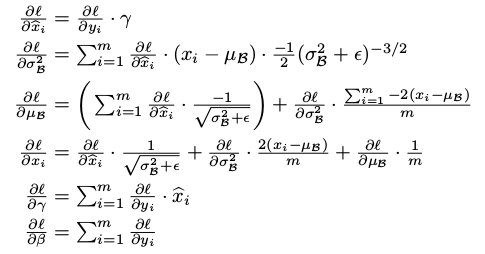BN层_晶圆bn层是什么

论文名字：Batch Normalization: Accelerating Deep Network Training by  Reducing Internal Covariate Shift

论文地址：https://arxiv.org/abs/1502.03167

BN被广泛应用于深度学习的各个地方，由于在实习过程中需要修改网络，修改的网络在训练过程中无法收敛，就添加了BN层进去来替换掉LRN层，网络可以收敛。现在就讲一下Batch Normalization的工作原理。

BN层和卷积层，池化层一样都是一个网络层。

首先我们根据论文来介绍一下BN层的优点

1）加快训练速度，这样我们就可以使用较大的学习率来训练网络。

2）提高网络的泛化能力。

3）BN层本质上是一个归一化网络层，可以替代局部响应归一化层（LRN层）。

4）可以打乱样本训练顺序（这样就不可能出现同一张照片被多次选择用来训练）论文中提到可以提高1%的精度。

前向计算和反向求导

在前向传播的时候：

从论文中给出的伪代码可以看出来BN层的计算流程是：

1.计算样本均值。

2.计算样本方差。

3.样本数据标准化处理。

4.进行平移和缩放处理。引入了γ和β两个参数。来训练γ和β两个参数。引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布。

在反向传播的时候，通过链式求导方式，求出γ与β以及相关权值 

怎么使用BN层

先解释一下对于图片卷积是如何使用BN层。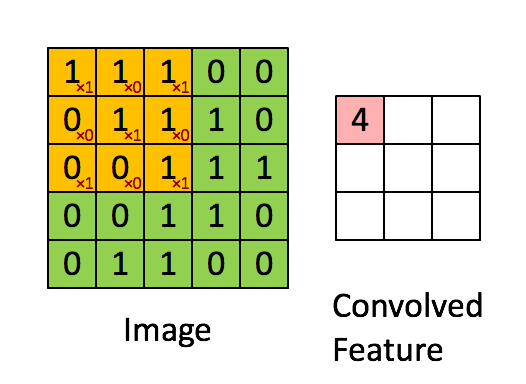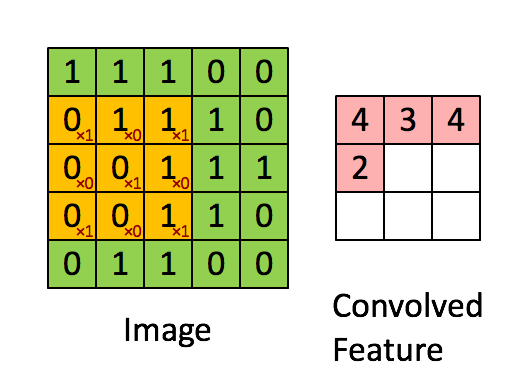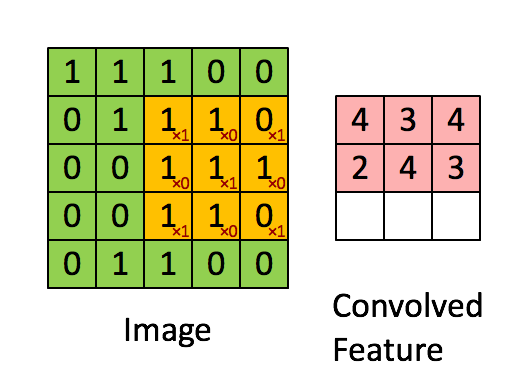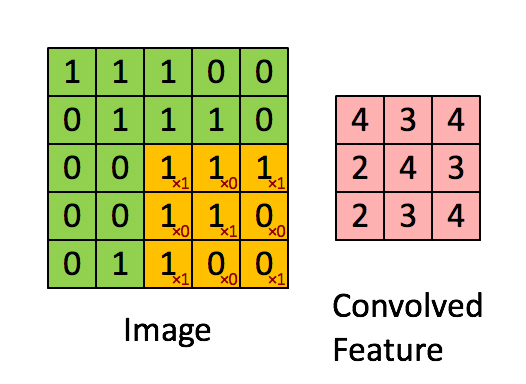 
 
这是文章卷积神经网络CNN（1）中5×5的图片通过valid卷积得到的3×3特征图（粉红色）。特征图里的值，作为BN的输入，也就是这9个数值通过BN计算并保存γ与β，通过γ与β使得输出与输入不变。假设输入的batch_size为m，那就有m*9个数值，计算这m*9个数据的γ与β并保存。正向传播过程如上述，对于反向传播就是根据求得的γ与β计算梯度。 
这里需要着重说明2个细节： 
1.网络训练中以batch_size为最小单位不断迭代，很显然，新的batch_size进入网络，即会有新的γ与β，因此，在BN层中，有总图片数/batch_size组γ与β被保存下来。 
2.图像卷积的过程中，通常是使用多个卷积核，得到多张特征图，对于多个的卷积核需要保存多个的γ与β。

结合论文中给出的使用过程进行解释 
 
输入：待进入激活函数的变量 
输出： 
1.对于K维的输入，假设每一维包含m个变量，所以需要K个循环。每个循环中按照上面所介绍的方法计算γ与β。这里的K维，在卷积网络中可以看作是卷积核个数，如网络中第n层有64个卷积核，就需要计算64次。 
需要注意，在正向传播时，会使用γ与β使得BN层输出与输入一样。 
2.在反向传播时利用γ与β求得梯度从而改变训练权值（变量）。 
3.通过不断迭代直到训练结束，求得关于不同层的γ与β。如网络有n个BN层，每层根据batch_size决定有多少个变量，设定为m，这里的mini-batcherB指的是特征图大小*batch_size，即m=特征图大小*batch_size，因此，对于batch_size为1，这里的m就是每层特征图的大小。 
4.不断遍历训练集中的图片，取出每个batch_size中的γ与β，最后统计每层BN的γ与β各自的和除以图片数量得到平均直，并对其做无偏估计直作为每一层的E[x]与Var[x]。 
5.在预测的正向传播时，对测试数据求取γ与β，并使用该层的E[x]与Var[x]，通过图中11:所表示的公式计算BN层输出。 
注意，在预测时，BN层的输出已经被改变，所以BN层在预测的作用体现在此处

BN层原理分析

1 训练数据为什么要和测试数据同分布？

看看下图，如果我们的网络在左上角的数据训练的，已经找到了两者的分隔面w，如果测试数据是右下角这样子，跟训练数据完全不在同一个分布上面，你觉得泛化能力能好吗？ 

2 为什么白化训练数据能够加速训练进程

如下图，训练数据如果分布在右上角，我们在初始化网络参数w和b的时候，可能得到的分界面是左下角那些线，需要经过训练不断调整才能得到穿过数据点的分界面，这个就使训练过程变慢了；如果我们将数据白化后，均值为0，方差为1，各个维度数据去相关，得到的数据点就是坐标上的一个圆形分布，如下图中间的数据点，这时候随便初始化一个w，b设置为0，得到的分界面已经穿过数据了，因此训练调整，训练进程会加快 

3、为什么BN层可以改善梯度弥散

下面xhat到x的梯度公式，可以表示为正常梯度乘一个系数a，再加b，这里加了个b，整体给梯度一个提升，补偿sigmod上的损失，改善了梯度弥散问题。 

4、为什么BN层一般用在线性层和卷积层后面，而不是放在非线性单元后

原文中是这样解释的，因为非线性单元的输出分布形状会在训练过程中变化，归一化无法消除他的方差偏移，相反的，全连接和卷积层的输出一般是一个对称,非稀疏的一个分布，更加类似高斯分布，对他们进行归一化会产生更加稳定的分布。其实想想也是的，像relu这样的激活函数，如果你输入的数据是一个高斯分布，经过他变换出来的数据能是一个什么形状？小于0的被抑制了，也就是分布小于0的部分直接变成0了，这样不是很高斯了。

5、BN起作用的原因

通过使得批量数据归一化具有0均值1方差的统计分布，避免数据处于激活函数的饱和区，具有较大的梯度，从而加速网络的训练过程。

减少了网络输入变化过大的问题，使得网络的输入稳定，减弱了与前层参数关系之间的作用，使得当前层独立于整个网络

BN具有轻微正则化的效果，可以和dropout一起使用

主要是归一化激活值前的隐藏单元来加速训练，正则化是副作用

6、BN具有正则化效果的原因

每个批量的数据仅根据当前批量计算均值和标准差，然后缩放

这就为该批量的激活函数带来了一些噪音，类似于dropout向每一层的激活函数带来噪音

若使用了较大的batch_size如512，则减小了噪音，减少了正则化带来的效果

参考文献：

https://blog.csdn.net/donkey_1993/article/details/81871132

https://blog.csdn.net/qq_29573053/article/details/79878437

https://www.cnblogs.com/kk17/p/9693462.html

https://blog.csdn.net/u012151283/article/details/78154917 

今天的文章BN层_晶圆bn层是什么分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。