角度和弧度的计算_三角函数和弧度制换算

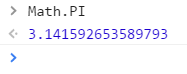
Math.PI 表示一个圆的周长与直径的比例，约为 3.141592653589793，其实就是我们所说的圆周率 π 

Math.sin(x) //x 的正玄值。返回值在 -1.0 到 1.0 之间；

Math.cos(x) //x 的余弦值。返回的是 -1.0 到 1.0 之间的数；

角度和弧度转换公式：

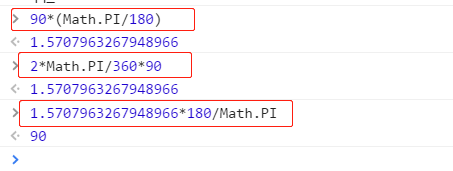
　　弧度 = 角度*PI/180 
　　角度 = 弧度*180/PI

还有一个计算弧度常用的：（一样的）

　　弧度的计算公式为： 2*PI/360*角度；

 验证：

弧度 = 角度 ×（PI/180）；

30° 角度 的弧度 = 30 * （PI/180）

案例一：根据半径获取圆周值

使用 Math.PI 计算给定半径的圆周长

function calculateCircumference (radius) {
  return 2 * Math.PI * radius;
}

calculateCircumference(1);  // 6.283185307179586

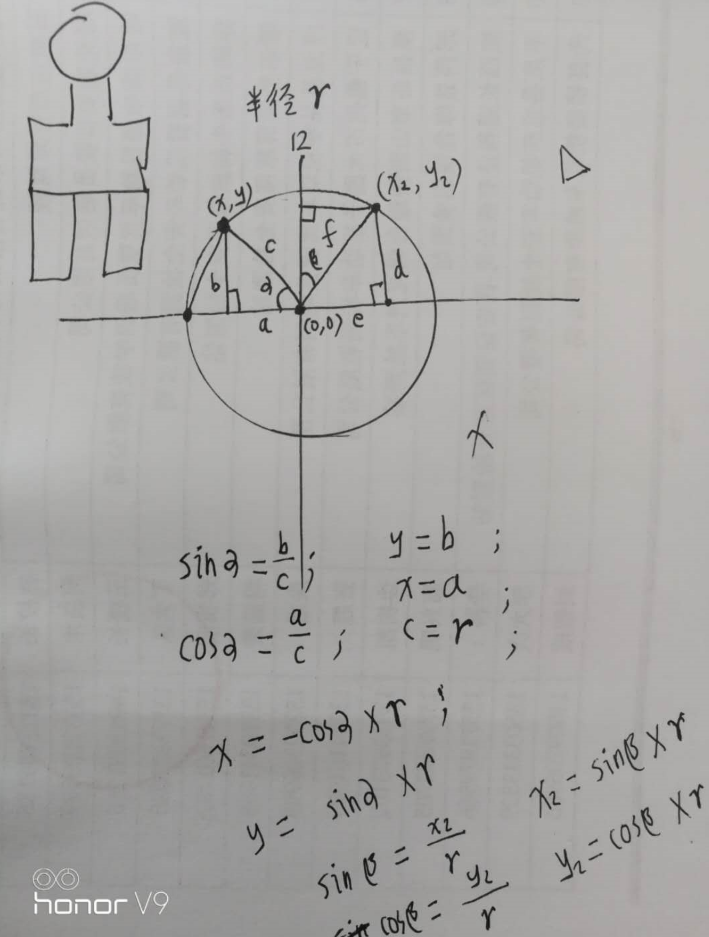
案例二：如何得到圆上每个点的坐标？

解决思路：根据三角形的正玄、余弦来得值；

假设一个圆的圆心坐标是(a,b)，半径为r

则圆上每个点的：

X坐标 = a + Math.sin(2*Math.PI / 360) * r  ；

Y坐标 = b + Math.cos(2*Math.PI / 360) * r  ；

———————————————————

如何得到圆上每个点的坐标？

解决思路：根据三角形的正玄、余弦来得值；

假设一个圆的圆心坐标是(a,b)，半径为r，

则圆上每个点的: 
X坐标=a + Math.sin(角度 * (Math.PI / 180)) * r ；
Y坐标=b + Math.cos(角度 * (Math.PI / 180)) * r ； 

每个人的习惯不一样……….

图解：

案例三：如何求时钟的秒针转动一圈的轨迹？

假设秒针的初始值（起点）为12点钟方向，圆心的坐标为（a,b)。

解决思路：一分钟为60秒，一个圆为360°，所以平均每秒的转动角度为 360°/60 = 6°； 

for(var times=0; times<60; times++) {

      var hudu = 6 * (Math.PI / 180) *  times;

       var X = a + Math.sin(hudu) * r;

       var Y = b – Math.cos(hudu) * r    //  注意此处是“-”号，因为我们要得到的Y是相对于（0,0）而言的。

}

注意：
1、本例是以“12点为起点, 角度增大时为顺时针方向“，求X坐标和Y坐标的方法是：
X坐标=a + Math.sin(角度 * (Math.PI / 180)) * r ；
Y坐标=b – Math.cos(角度 * (Math.PI / 180)) * r ； 

2、一般“3点为起点, 角度增大时为逆时针方向“，求X坐标和Y坐标的方法是：
X坐标 = a + Math.cos(角度 * (Math.PI / 180)) * r;    
Y坐标 = b – Math.sin(角度 * (Math.PI / 180)) * r;    

角度与弧度互转（比较好的文章内容）

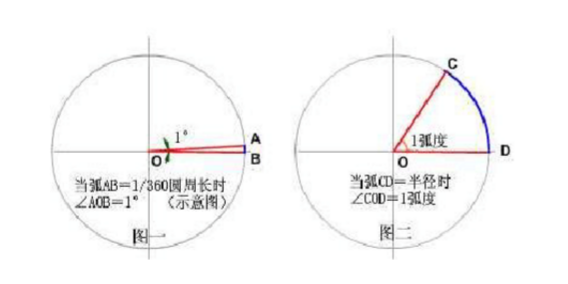
1、角度定义
     两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当弧长正好等于圆周长的360分之一时，两条射线的夹角的大小为1度。(单位: º）

2、弧度定义
     两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时，两条射线的夹角大小为1弧度（单位：rad)。
可简单理解为：弧度 = 弧长 / 半径

3、弧长与弧度
     3.1 圆的周长C的计算公式为：C = 2πr = πd    (r – 半径；d – 直径)
     3.2 圆一周的弧长为：2πr                    (弧长 = 周长）
     3.2 圆一周的弧度为：2πr / r = 2π                  (根据：弧度 = 弧长 / 半径） 

4、度与角度的转换
   根据圆为360 º，弧度为2π，即 360º = 2π 

   4.1 角度转弧度：2π / 360  = π / 180 ≈ 0.0174rad, 即: 度数 * (π / 180） = 弧度
   例如：将30º转为弧度rad 
   30º * (π / 180）= 0.523320 rad 
 
   4.2 弧度转角度: 360 / 2π  = 180 / π ≈ 57.3º,  即:  弧度 * (180 / π） = 度数
   例如：将0.523320rad转为度º
   0.523320rad * (180 / π) = 29.9992352688º 

参考：

http://t.zoukankan.com/xiejn-p-11901019.html

今天的文章角度和弧度的计算_三角函数和弧度制换算分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。