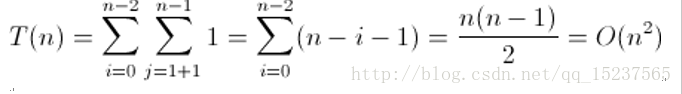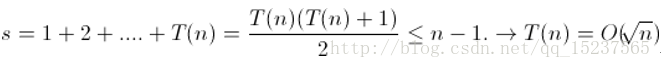一、概念

时间复杂度是总运算次数表达式中受n的变化影响最大的那一项(不含系数)
比如：一般总运算次数表达式类似于这样：
a*2^n+b*n^3+c*n^2+d*n*lg(n)+e*n+f
a ！ =0时，时间复杂度就是O(2^n);
a=0,b<>0 =>O(n^3);
a,b=0,c<>0 =>O(n^2)依此类推

eg:

(1)   for(i=1;i<=n;i++)   //循环了n*n次，当然是O(n^2)
            for(j=1;j<=n;j++)
                 s++;
(2)   for(i=1;i<=n;i++)//循环了(n+n-1+n-2+...+1)≈(n^2)/2，因为时间复杂度是不考虑系数的，所以也是O(n^2)
            for(j=i;j<=n;j++)
                 s++;
(3)   for(i=1;i<=n;i++)//循环了(1+2+3+...+n)≈(n^2)/2,当然也是O(n^2)
            for(j=1;j<=i;j++)
                 s++;
(4)   i=1;k=0;

      while(i<=n-1){

           k+=10*i;

i++; }

//循环了

n-1≈n次，所以是O(n)

(5) for(i=1;i<=n;i++)

             for(j=1;j<=i;j++)

                 for(k=1;k<=j;k++)

                       x=x+1;

//

循环了(1^2+2^2+3^2+...+n^2)=n(n+1)(2n+1)/6(这个公式要记住哦)≈(n^3)/3，不考虑系数，自然是O(n^3)

另外，在时间复杂度中，log(2,n)(以2为底)与lg(n)(以10为底)是等价的，因为对数换底公式：

log(a,b)=log(c,b)/log(c,a)
所以，log(2,n)=log(2,10)*lg(n),忽略掉系数，二者当然是等价的

二、计算方法

1.一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2.一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f（n），因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，所以f（n）越小，算法的时间复杂度越低，算法的效率越高。

在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

3.常见的时间复杂度

按数量级递增排列，常见的时间复杂度有：

常数阶O(1),  对数阶O(log2n),  线性阶O(n),  线性对数阶O(nlog2n),  平方阶O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k), 指数阶O(2^n) 。

其中，

1.O(n)，O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度。。。。

2.O(2^n)，指数阶时间复杂度，该种不实用

3.对数阶O(log2n),   线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高

例：算法：
  for（i=1;i<=n;++i）
  {
     for(j=1;j<=n;++j)
     {
         c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2

          for(k=1;k<=n;++k)
               c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
     }
  }
  则有 T（n）= n^2+n^3，根据上面括号里的同数量级，我们可以确定 n^3为T（n）的同数量级
  则有f（n）= n^3，然后根据T（n）/f（n）求极限可得到常数c
  则该算法的 时间复杂度：T（n）=O（n^3)

四、

定义：如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)，它是n的某一函数 T(n)称为这一算法的“时间复杂性”。

当输入量n逐渐加大时，时间复杂性的极限情形称为算法的“渐近时间复杂性”。

我们常用大O表示法表示时间复杂性，注意它是某一个算法的时间复杂性。大O表示只是说有上界，由定义如果f(n)=O(n)，那显然成立f(n)=O(n^2)，它给你一个上界，但并不是上确界，但人们在表示的时候一般都习惯表示前者。

此外，一个问题本身也有它的复杂性，如果某个算法的复杂性到达了这个问题复杂性的下界，那就称这样的算法是最佳算法。

“大O记法”：在这种描述中使用的基本参数是 n，即问题实例的规模，把复杂性或运行时间表达为n的函数。这里的“O”表示量级 (order)，比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”记法 O ( f(n) )表示当 n增大时，运行时间至多将以正比于 f(n)的速度增长。

这种渐进估计对算法的理论分析和大致比较是非常有价值的，但在实践中细节也可能造成差异。例如，一个低附加代价的O(n2)算法在n较小的情况下可能比一个高附加代价的 O(nlogn)算法运行得更快。当然，随着n足够大以后，具有较慢上升函数的算法必然工作得更快。

O(1)

Temp=i;i=j;j=temp;

以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=O(1)。如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。

O(n^2)

2.1. 交换i和j的内容

     sum=0；                 （一次）

     for(i=1;i<=n;i++)       （n次）

        for(j=1;j<=n;j++) （n^2次）

         sum++；       （n^2次）

解：T(n)=2n^2+n+1 =O(n^2)

2.2.

    for (i=1;i<n;i++)

    {

        y=y+1;         ①

        for (j=0;j<=(2*n);j++)

           x++;        ②

    }

解：语句1的频度是n-1

          语句2的频度是(n-1)*(2n+1)=2n^2-n-1

          f(n)=2n^2-n-1+(n-1)=2n^2-2

          该程序的时间复杂度T(n)=O(n^2).

O(n)



2.3.

    a=0;

    b=1;                      ①

    for (i=1;i<=n;i++) ②

    {

       s=a+b;　　　　③

       b=a;　　　　　④

       a=s;　　　　　⑤

    }

解：语句1的频度：2,

           语句2的频度： n,

          语句3的频度： n-1,

          语句4的频度：n-1,

          语句5的频度：n-1,

          T(n)=2+n+3(n-1)=4n-1=O(n).



O(log2n )

2.4.

     i=1;       ①

    while (i<=n)

       i=i*2; ②

解：语句1的频度是1,

          设语句2的频度是f(n),   则：2^f(n)<=n;f(n)<=log2n

          取最大值f(n)= log2n,

          T(n)=O(log2n )

O(n^3)

2.5.

    for(i=0;i<n;i++)

    {

       for(j=0;j<i;j++)

       {

          for(k=0;k<j;k++)

             x=x+2;

       }

    }

解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,…,m-1 , 所以这里最内循环共进行了0+1+…+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+…+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).

我们还应该区分算法的最坏情况的行为和期望行为。如快速排序的最坏情况运行时间是 O(n^2)，但期望时间是 O(nlogn)。通过每次都仔细地选择基准值，我们有可能把平方情况 (即O(n^2)情况)的概率减小到几乎等于 0。在实际中，精心实现的快速排序一般都能以 (O(nlogn)时间运行。

下面是一些常用的记法：

访问数组中的元素是常数时间操作，或说O(1)操作。一个算法如果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。用strcmp比较两个具有n个字符的串需要O(n)时间。常规的矩阵乘算法是O(n^3)，因为算出每个元素都需要将n对元素相乘并加到一起，所有元素的个数是n^2。

指数时间算法通常来源于需要求出所有可能结果。例如，n个元素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。指数算法一般说来是太复杂了，除非n的值非常小，因为，在这个问题中增加一个元素就导致运行时间加倍。不幸的是，确实有许多问题 (如著名的“巡回售货员问题” )，到目前为止找到的算法都是指数的。如果我们真的遇到这种情况，通常应该用寻找近似最佳结果的算法替代之。

https://blog.csdn.net/firefly_2002/article/details/8008987

https://blog.csdn.net/qq_15237565/article/details/77885311

数据结构中的时间复杂度的计算

算法的时间复杂度定义为：

时间复杂度或称时间复杂性，又称计算复杂度，她说是算法有效的度量之一，时间复杂度是一个算法运行时间的相对度量，一个算法的运行时间长短，它大致等于执行一种简单操作所（赋值、比较、计算、转向、返回、输入和输出）需要的时间与算法中进行简单操作次数的乘积。

根据定义，求解算法的时间复杂度的具体步骤是：

⑴ 找出算法中的基本语句；
　　一般算法中执行次数最多的那条语句就是基本语句，通常是最内层循环的循环体。

⑵ 计算基本语句的执行次数的数量级；
　　只需计算基本语句执行次数的数量级，这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可，可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析，并且使注意力集中在最重要的一点上：增长率。

⑶ 用大Ο记号表示算法的时间性能。
　　当n趋近于无穷大时，如果lim(T(n)/f(n))的值为不等于0的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))。

简单的说，就是保留求出次数的最高次幂，并且把系数去掉。如T(n)=2n^2+n+1=O(n^2)

举个例子：

#include “stdio.h”
int main()
{
int i, j, x = 0, sum = 0, n = 100; /* 执行1次 */
for( i = 1; i <= n; i++) /* 执行n+1次 */
{
sum = sum + i;
/* 执行n次 */
for( j = 1; j <= n; j++) /* 执行n*(n+1)次 */
{
x++;
/* 执行n*n次 */
sum = sum + x;
/* 执行n*n次 */
}
}
printf(“%d”, sum); /* 执行1次 */
}

照上面推导“大O阶”的步骤，我们来看

第一步：“用常数 1 取代运行时间中的所有加法常数”，

则上面的算式变为：执行总次数 =3n^2 + 3n + 1

（直接相加的话,应该是T(n) = 1 + n+1 + n +n*(n+1) + n*n + n*n + 1 = 3n^2 + 3n + 3。现在用常数 1 取代运行时间中的所有加法常数，就是把T(n) =3n^2 + 3n + 3中的最后一个3改为1. 就得到了 T(n) = 3n^2 + 3n + 1）

第二步：“在修改后的运行次数函数中，只保留最高阶项”。

这里的最高阶是 n 的二次方，所以算式变为：执行总次数 = 3n^2

第三步：“如果最高阶项存在且不是 1 ，则去除与这个项相乘的常数”。

这里 n 的二次方不是 1 所以要去除这个项的相乘常数，算式变为：执行总次数 = n^2
因此最后我们得到上面那段代码的算法时间复杂度表示为： O( n^2 )

下面我把常见的算法时间复杂度以及他们在效率上的高低顺序记录在这里，使大家对算法的效率有个直观的认识。

O(1) 常数阶 < O(logn) 对数阶 < O(n) 线性阶 < O(nlogn) < O(n^2) 平方阶 < O(n^3) < { O(2^n) < O(n!) <O(n^n) }

最后三项用大括号把他们括起来是想要告诉大家，如果日后大家设计的算法推导出的“大O阶”是大括号中的这几位，那么趁早放弃这个算法，在去研究新的算法出来吧。因为大括号中的这几位即便是在 n 的规模比较小的情况下仍然要耗费大量的时间，算法的时间复杂度大的离谱，基本上就是“不可用状态。

好了，原理就介绍到这里了。下面通过几个例子具体分析下时间复杂度计算过程。

一、计算
1 + 2 + 3 + 4 + …… + 100。

常规代码：

#include “stdio.h”
int main()
{
int i, sum = 0, n = 100; /* 执行1次 */
for( i = 1; i <= n; i++) /* 执行 n+1 次 */
{
sum = sum + i;
/* 执行n次 */
//printf(“%d \n”, sum);
}
printf(“%d”, sum); /* 执行1次 */
}

从代码附加的注释可以看到所有代码都执行了多少次。那么这写代码语句执行次数的总和就可以理解为是该算法计算出结果所需要的时间。该算法所用的时间（算法语句执行的总次数）为：
1 + ( n + 1 ) + n + 1 = 2n + 3

而当 n 不断增大，比如我们这次所要计算的不是 1 + 2 + 3 + 4 +…… + 100 = ？而是 1 + 2 + 3 + 4 + …… + n = ？其中 n 是一个十分大的数字，那么由此可见，上述算法的执行总次数（所需时间）会随着 n 的增大而增加，但是在 for 循环以外的语句并不受 n 的规模影响（永远都只执行一次）。所以我们可以将上述算法的执行总次数简单的记做： 2n 或者简记 n

这样我们就得到了我们设计的算法的时间复杂度，我们把它记作： O(n)。

高斯算法：

#include “stdio.h”
int main()
{
int sum = 0, n = 100; /* 执行1次 */
sum = (
1 + n) * n/2; /* 执行1次 */

printf(“%d”, sum); /* 执行1次 */
}

这个算法的时间复杂度： O(3)，但一般记作 O(1)。
从感官上我们就不难看出，从算法的效率上看，O(1) < O(n) 的，所以高斯的算法更快，更优秀。

二、求两个
n 阶方阵 C=A*B 的乘积其算法如下 :

//右边列为语句执行的频度
void MatrixMultiply(int A[n][n]，int B [n][n]，int C[n][n])
{
for(int i=0; i <n; i++) //n+1
{
for (j=0;j < n; j++) //n*(n+1)
{
C[i][j]=
0; //n^2
for (k=0; k<n; k++) //n^2*(n+1)
{
C[i][j]=C[i][j]+A[i][k]*B[k][j];
//n^3
}
}
}
}

则该算法所有语句的频度之和为:
T(n) = 2n^3+3n^2+2n+1; 利用大O表示法,该算法的时间复杂度为O(n^3)。

三、分析下列时间复杂度

void test_(int n)
{
i =
1, k = 100;
while (i<n)
{
k = k +
1;
i +=
2;
}
}

设for循环语句执行次数为T(n),则 i = 2T(n) + 1 <= n – 1, 即T(n) <= n/2 – 1 = O(n)

四、分析下列时间复杂度

void test_2(int b[]， int n)
{
int i, j, k;
for (i=0; i<n-1; i++)
{
k = i;
for (j=i+1; j<n; j++)
{
if (b[k] > b[j])
{
k = j;
}
}
x = b[i];
b[i] = b[k];
b[k] = x;
}
}

其中，算法的基本运算语句是

if (b[k] > b[j])

{

k = j;

}

其执行次数T(n)为：

五、分析下列时间复杂度

void test_3(int n)
{
int i = 0, s = 0;
while (s<n)
{
i++;
s = s + i;
}
}

其中，算法的基本运算语句即while循环内部分，

设 while 循环语句执行次数为 T(n), 则

六、Hanoi(递归算法)时间复杂度分析

void hanoi(int n, char a, char b, char c)
{
if (n==1)
{
printf(“move %d disk from %c to %c \n”, n, a, c); //执行一次
}
else
{
hanoi(n
-1, a, c, b); //递归n-1次
printf(“move %d disk from %c to %c \n”, n, a, c); //执行一次
hanoi(n
-1, b, a, c); //递归n-1次
}
}

对于递归函数的分析,跟设计递归函数一样，要先考虑基情况(比如hanoi中n==1时候),这样把一个大问题划分为多个子问题的求解。

故此上述算法的时间复杂度的递归关系如下
:

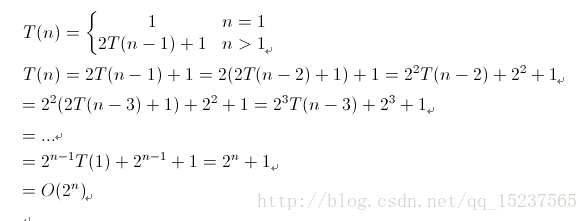
今天的文章如何计算时间复杂度和空间复杂度_时间复杂度计算的例题讲解分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/53063.html

如何计算时间复杂度和空间复杂度_时间复杂度计算的例题讲解

数据结构中的时间复杂度的计算

相关推荐

发表回复