ssim算法原理 – 我们都不是神的孩子 – CSDN博客 http://blog.csdn.net/ecnu18918079120/article/details/60149864
一、结构相似性(structural similarity)
自然图像具有极高的结构性,表现在图像的像素间存在着很强的相关性,尤其是在空间相似的情况下。这些相关性在视觉场景中携带着关于物体结构的重要信息。我们假设人类视觉系统(HSV)主要从可视区域内获取结构信息。所以通过探测结构信息是否改变来感知图像失真的近似信息。
大多数的基于误差敏感度(error sensitivity)的质量评估方法(如MSE,PSNR)使用线性变换来分解图像信号,这不会涉及到相关性。我们要讨论的SSIM就是要找到更加直接的方法来比较失真图像和参考图像的结构。
二、SSIM指数
物体表面的亮度信息与照度和反射系数有关,且场景中的物体的结构与照度是独立的,反射系数与物体有关。我们可以通过分离照度对物体的影响来探索一张图像中的结构信息。这里,把与物体结构相关的亮度和对比度作为图像中结构信息的定义。因为一个场景中的亮度和对比度总是在变化的,所以我们可以通过分别对局部的处理来得到更精确的结果。
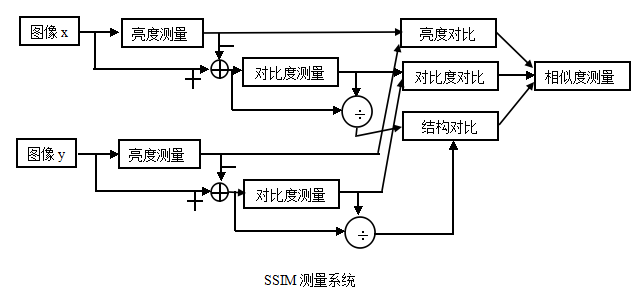
由SSIM测量系统可得相似度的测量可由三种对比模块组成,分别为:亮度,对比度,结构。接下来我们将会对这三模块函数进行定义。
首先,对于离散信号,我们以平均灰度来作为亮度测量的估计:
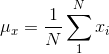 (1)
(1) 亮度对比函数l(x,y)是关于 的函数。
的函数。
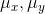 的函数。
的函数。 然后,由测量系统知道要把平均灰度值从信号中去除,对于离散信号 ,可使用标准差来做对比度估量值。
,可使用标准差来做对比度估量值。
 ,可使用标准差来做对比度估量值。
,可使用标准差来做对比度估量值。 (2)
(2) 对比度对比函数c(x,y)就是 的函数。
的函数。
 的函数。
的函数。 接下来,信号被自己的标准差相除,结构对比函数就被定义成 和
和 的函数。
的函数。
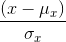 和
和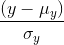 的函数。
的函数。 最后,三个对比模块组合成一个完整的相似测量函数:
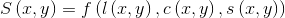 (3)
(3) S(x,y)应该满足以下三个条件:
(1) 对称性: ;
;
 ;
; (2) 有界性: ;
;
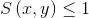 ;
; (3) 最大值唯一性:当且仅当x=y时,S(x,y)=1 。
现在,我们定义三个对比函数。
亮度对比函数:
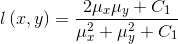 (4)
(4) 常数 是为了避免
是为了避免 接近0时造成系统的不稳定。
接近0时造成系统的不稳定。
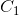 是为了避免
是为了避免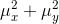 接近0时造成系统的不稳定。
接近0时造成系统的不稳定。 特别的,我们选择 ,L为图像灰度级数,对于8-bit灰度图像,L=255,
,L为图像灰度级数,对于8-bit灰度图像,L=255, 。公式(4)满足上述三个条件。
。公式(4)满足上述三个条件。
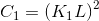 ,L为图像灰度级数,对于8-bit灰度图像,L=255,
,L为图像灰度级数,对于8-bit灰度图像,L=255,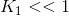 。公式(4)满足上述三个条件。
。公式(4)满足上述三个条件。 对比度对比函数:
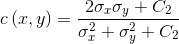 (5)
(5) 常数 ,且
,且 。公式(5)依然满足上述三个条件。
。公式(5)依然满足上述三个条件。
 ,且
,且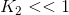 。公式(5)依然满足上述三个条件。
。公式(5)依然满足上述三个条件。 结构对比函数:
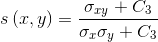 (6)
(6) 其中
 (7)
(7) 最后把三个函数组合起来,得到SSIM指数函数:
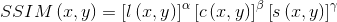 (8)
(8) 这里 ,用来调整三个模块间的重要性。
,用来调整三个模块间的重要性。
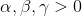 ,用来调整三个模块间的重要性。
,用来调整三个模块间的重要性。 为了得到简化形式,设 ,得到:
,得到:
 ,得到:
,得到: (9)
(9)三、SSIM指数应用于图像质量评估
在图像质量评估之中,局部求SSIM指数的效果要好于全局。第一,图像的统计特征通常在空间中分布不均;第二,图像的失真情况在空间中也是变化的;第三,在正常视距内,人们只能将视线聚焦在图像的一个区域内,所以局部处理更符合人类视觉系统的特点;第四,局部质量检测能得到图片空间质量变化的映射矩阵,结果可服务到其他应用中。
所以,在上述公式中, 都加入了一个8*8的方形窗,并且逐像素的遍历整幅图片。每一步计算,
都加入了一个8*8的方形窗,并且逐像素的遍历整幅图片。每一步计算, 和SSIM都是基于窗口内像素的,最终得到一个SSIM指数映射矩阵,由局部SSIM指数组成。然而,简单的加窗会使映射矩阵出现不良的“分块”效应。为解决这问题,我们使用11*11的对称高斯加权函数
和SSIM都是基于窗口内像素的,最终得到一个SSIM指数映射矩阵,由局部SSIM指数组成。然而,简单的加窗会使映射矩阵出现不良的“分块”效应。为解决这问题,我们使用11*11的对称高斯加权函数 作为加权窗口,标准差为1.5,且
作为加权窗口,标准差为1.5,且
 都加入了一个8*8的方形窗,并且逐像素的遍历整幅图片。每一步计算,
都加入了一个8*8的方形窗,并且逐像素的遍历整幅图片。每一步计算, 和SSIM都是基于窗口内像素的,最终得到一个SSIM指数映射矩阵,由局部SSIM指数组成。然而,简单的加窗会使映射矩阵出现不良的“分块”效应。为解决这问题,我们使用11*11的对称高斯加权函数
和SSIM都是基于窗口内像素的,最终得到一个SSIM指数映射矩阵,由局部SSIM指数组成。然而,简单的加窗会使映射矩阵出现不良的“分块”效应。为解决这问题,我们使用11*11的对称高斯加权函数 作为加权窗口,标准差为1.5,且
作为加权窗口,标准差为1.5,且 (10)
(10)则 的估计值表示为:
的估计值表示为:
 的估计值表示为:
的估计值表示为: (11)
(11) (12)
(12) (13)
(13) 应用这种加窗方法,映射矩阵就可展现出局部各向同性的性质。
在这里,经过一些实验总结,我们把K1设为0.01,K2设为0.03,然后用平均SSIM指数作为整幅图像的估计质量评价:
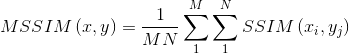 (14)
(14)其中X,Y为图像, 为局部SSIM指数在映射中的位置,MN为局部窗口的数量。
为局部SSIM指数在映射中的位置,MN为局部窗口的数量。
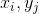 为局部SSIM指数在映射中的位置,MN为局部窗口的数量。
为局部SSIM指数在映射中的位置,MN为局部窗口的数量。四、matlab实现
- function [mssim, ssim_map,siga_sq,sigb_sq] = SSIM(ima, imb)
- % ========================================================================
- %ssim的算法主要参考如下论文:
- %Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image
- % quality assessment: From error visibility to structural similarity,”
- % IEEE Transactios on Image Processing, vol. 13, no. 4, pp. 600-612,
- % Apr. 2004.
- % 首先对图像加窗处理,w=fspecial(‘gaussian’, 11, 1.5);
- % (2*ua*ub+C1)*(2*sigmaa*sigmab+C2)
- % SSIM(A,B)=————————————————————————
- % (ua*ua+ub*ub+C1)(sigmaa*sigmaa+sigmab*sigmab+C2)
- % C1=(K1*L);
- % C2=(K2*L); K1=0.01,K2=0.03
- % L为灰度级数,L=255
- %——————————————————————-
- % ima – 比较图像A
- % imb – 比较图像B
- %
- % ssim_map – 各加窗后得到的SSIM(A,B|w)组成的映射矩阵
- % mssim – 对加窗得到的SSIM(A,B|w)求平均,即最终的SSIM(A,B)
- % siga_sq – 图像A各窗口内灰度值的方差
- % sigb_sq – 图像B各窗口内灰度值的方差
- %——————————————————————-
- % Cool_ben
- %========================================================================
- w = fspecial(‘gaussian’, 11, 1.5); %window 加窗
- K(1) = 0.01;
- K(2) = 0.03;
- L = 255;
- ima = double(ima);
- imb = double(imb);
- C1 = (K(1)*L)^2;
- C2 = (K(2)*L)^2;
- w = w/sum(sum(w));
- ua = filter2(w, ima, ‘valid’);%对窗口内并没有进行平均处理,而是与高斯卷积,
- ub = filter2(w, imb, ‘valid’); % 类似加权平均
- ua_sq = ua.*ua;
- ub_sq = ub.*ub;
- ua_ub = ua.*ub;
- siga_sq = filter2(w, ima.*ima, ‘valid’) – ua_sq;
- sigb_sq = filter2(w, imb.*imb, ‘valid’) – ub_sq;
- sigab = filter2(w, ima.*imb, ‘valid’) – ua_ub;
- ssim_map = ((2*ua_ub + C1).*(2*sigab + C2))./((ua_sq + ub_sq + C1).*(siga_sq + sigb_sq + C2));
- mssim = mean2(ssim_map);
- return
