一、简介
图像归一化是计算机视觉、模式识别等领域广泛使用的一种技术。所谓图像归一化, 就是通过一系列变换, 将待处理的原始图像转换成相应的唯一标准形式(该标准形式图像对平移、旋转、缩放等仿射变换具有不变特性)。 近年来, 基于矩的图像归一化技术受到了人们的普遍关注, 其基本工作原理为: 首先利用图像中对仿射变换具有不变性的矩来确定变换函数的参数, 然后利用此参数确定的变换函数把原始图像变换为一个标准形式的图像(该图像与仿射变换无关)。 一般说来, 基于矩的图像归一化过程包括 4 个步骤 即坐标中心化、x-shearing 归一化、缩放归一化和旋转归一化。
基本上归一化思想是利用图像的不变矩寻找一组参数使其能够消除其他变换函数对图像变换的影响。也就是转换成唯一的标准形式以抵抗仿射变换。图像归一化使得图像可以抵抗几何变换的攻击,它能够找出图像中的那些不变量,从而得知这些图像原本就是一样的或者一个系列的。以下你要知道的:
1.归一化处理并没有改变图像的对比度
2.归一化处理很简单,假设原图像是8位灰度图像,那么读入的像素矩阵最大值为256,最小值为1,定义矩阵为I,J=I/256,就是归一化的图像矩阵,就是说归一化之后所有的像素值都在[0,1]区间内。
二、什么是归一化
归一化就是通过一系列变换(即利用图像的不变矩寻找一组参数使其能够消除其他变换函数对图像变换的影响),将待处理的原始图像转换成相应的唯一标准形式(该标准形式图像对平移、旋转、缩放等仿射变换具有不变特性)。
基于矩的图像归一化技术基本工作原理为:首先利用图像中对仿射变换具有不变性的矩来确定变换函数的参数, 然后利用此参数确定的变换函数把原始图像变换为一个标准形式的图像(该图像与仿射变换无关)。 一般说来,基于矩的图像归一化过程包括4个步骤,即坐标中心化、x-shearing 归一化、缩放归一化和旋转归一化。
图像归一化使得图像可以抵抗几何变换的攻击,它能够找出图像中的那些不变量,从而得知这些图像原本就是一样的或者一个系列的。
三、为什么归一化
1.基本上归一化思想是利用图像的不变矩寻找一组参数使其能够消除其他变换函数对图像变换的影响。也就是转换成唯一的标准形式以抵抗仿射变换。图像归一化使得图像可以抵抗几何变换的攻击,它能够找出图像中的那些不变量,从而得知这些图像原本就是一样的或者一个系列的。
2.matlab里图像数据有时候必须是浮点型才能处理,而图像数据本身是0-255的UNIT型数据所以需要归一化,转换到0-1之间。
3.归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。目的是为了:
(1)避免具有不同物理意义和量纲的输入变量不能平等使用
(2)bp中常采用sigmoid函数作为转移函数,归一化能够防止净输入绝对值过大引起的神经元输出饱和现象
(3)保证输出数据中数值小的不被吞食
3.神经网络中归一化的原因:
归一化是为了加快训练网络的收敛性,可以不进行归一化处理;
归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布,归一化在-1–+1之间是统计的坐标分布。归一化有同一、统一和合一的意思。无论是为了建模还是为了计算,首先基本度量单位要同一,神经网络是以样本在事件中的统计分别几率来进行训练(概率计算)和预测的,归一化是同一在0-1之间的统计概率分布;当所有样本的输入信号都为正值时,与第一隐含层神经元相连的权值只能同时增加或减小,从而导致学习速度很慢。为了避免出现这种情况,加快网络学习速度,可以对输入信号进行归一化,使得所有样本的输入信号其均值接近于0或与其均方差相比很小。
归一化是因为sigmoid函数的取值是0到1之间的,网络最后一个节点的输出也是如此,所以经常要对样本的输出归一化处理。所以这样做分类的问题时用[0.9 0.1 0.1]就要比用[1 0 0]要好。
但是归一化处理并不总是合适的,根据输出值的分布情况,标准化等其它统计变换方法有时可能更好。
四、matlab图像处理如何归一化
matlab中的归一化处理有三种方法
1. premnmx、postmnmx、tramnmx、mapminmax
(1)premnmx函数用于将网络的输入数据或输出数据进行归一化,归一化后的数据将分布在[-1,1]区间内。
premnmx语句的语法格式是:[Pn,minp,maxp,Tn,mint,maxt]=premnmx(P,T),其中P,T分别为原始输入和输出数据。
在训练网络时如果所用的是经过归一化的样本数据,那么以后使用网络时所用的新数据也应该和样本数据接受相同的预处理,这就要用到tramnmx函数:
(2)tramnmx语句的语法格式是:[PN]=tramnmx(P,minp,maxp)
其中P和PN分别为变换前、后的输入数据,maxp和minp分别为premnmx函数找到的最大值和最小值。
网络输出结果需要进行反归一化还原成原始的数据,常用的函数是:postmnmx。
(3)postmnmx语句的语法格式是:[PN] = postmnmx(P,minp,maxp)
其中P和PN分别为变换前、后的输入数据,maxp和minp分别为premnmx函数找到的最大值和最小值。
(4)还有一个函数是mapminmax,该函数可以把矩阵的每一行归一到[-1 1].
mapminmax语句的语法格式是:[y1,PS] = mapminmax(x1),其中x1 是需要归一的矩阵 y1是结果。
当需要对另外一组数据做归一时,就可以用下面的方法做相同的归一了
y2 = mapminmax(‘apply’,x2,PS)
当需要把归一的数据还原时,可以用以下命令:
x1_again = mapminmax(‘reverse’,y1,PS)
1> 默认的map范围是[-1, 1],所以如果需要[0, 1],则按这样的格式提供参数: MappedData = mapminmax(OriginalData, 0, 1); 2> 只按行归一化,如果是矩阵,则每行各自归一化;
3> 如果需要对整个矩阵归一化,用如下方法: FlattenedData = OriginalData(:)'; % 展开矩阵为一列,然后转置为一行。 MappedFlattened = mapminmax(FlattenedData, 0, 1); % 归一化。 MappedData = reshape(MappedFlattened, size(OriginalData)); % 还原为原始矩阵形式。此处不需转置回去,因为reshape恰好是按列重新排序
三种归一化方法:
除以序列最大值的,叫峰归一化;
除以序列之和的,叫面积归一化;
除以序列的模,叫数值归一化,得到序列的方差为0,均值为1;
(1) 线性函数转换,表达式如下:
y=(x-MinValue)/(MaxValue-MinValue)
y=0.1+(x-min)/(max-min)*(0.9-0.1)(归一到0.1-0.9之间)
说明:x、y分别为转换前、后的值,MaxValue、MinValue分别为样本的最大值和最小值。
(2) 对数函数转换,表达式如下:
y=log10(x)
说明:以10为底的对数函数转换。
(3) 反余切函数转换,表达式如下:
y=atan(x)*2/PI
(4) Z-score标准化方法
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
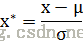
其中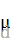
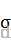
(5)一个归一化代码.
I = double(I);
maxvalue = max(max(I)’);
%max在把矩阵每列的最大值找到,并组成一个单行的数组,转置一下就会行转换为列,再max就求一个最大的值,如果不转置,只能求出每列的最大值。
f = 1 – I/maxvalue; %为什么要用1去减?
Image1 = f;
参考:http://blog.csdn.net/yihaizhiyan/article/details/6696912
http://blog.sina.com.cn/s/blog_675eb4fd01012chi.html
http://blog.sina.com.cn/s/blog_4aee288a0100ibt3.html
今天的文章图像归一化_函数归一化分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/53821.html
