概率算法
概率算法
什么是概率算法?
常见类型算法例如分治法、贪心算法、动态规划、回溯法和分支限界算法基本都属于确定性算法。即每一计算步骤都是确定的,而且在最后一定会返回一个确定的解。概率算法允许算法在每一步的执行过程中都可以随机的选择下一个计算步骤,所以在最后不一定能得到解。概率算法的一个重要特征就是,对所求解的同一实例使用同一算法求解多次,其结果可能是不同的,而且求解的时间也可能会有较大的差异。
为什么使用概率算法?
在较短的时间得到误差能被接受的解。现实生活中,有些问题的解并不一定要求是十分精确的,只要所求解和精确解的差值控制在一定范围之内,也是可以接受的。此时,用较短的时间得到解就十分必要。虽然确定性算法能够得到很好的解,但是存在某些确定性算法的时间复杂度很高。在许多情况下,算法在执行过程中面临一个选择时,随机选择通常比最优选择省时。因此,概率算法可以在很大程度上降低算法复杂度。
概率算法的类型
一般情况下,可将概率算法大致分为四类:数值概率算法,蒙特卡罗(Monte Carlo)算法,拉斯维加斯(Las Vegas)算法和舍伍德(Sherwood)算法。
随机数
在正式介绍概率算法之前,我们有必要讨论一下“随机数”。既然是概率算法,那么随机数的选择在其中的角色就至关重要。随机数指随机实验中的结果,具有不可预测性。由于概率算法中使用的随机数是由确定性算法所产生的,所以并不是严格意义上的随机数,此类随机数一般称为伪随机数。但由于伪随机数一般也会存在随机数的统计特征,所以一般用伪随机数替代真正的随机数。常见的伪随机数产生算法有线性同余法。
线性同余法(LCG)
线性同余法的递推公式为:Xn = ( A * Xn-1 +C ) % M ,其中,最重要的是关于三个值A,C,M的确定。LCG的最大周期为M,即所产生随机数的范围。
LCG的C++简单算法如下:
#include<iostream> using namespace std; void LCG(int num, int seed){ int A = 97; int C = 3; int M = 1000; int i = 1; while(i<=num){ seed = (A * seed+ C ) % M; cout << seed << endl; i++; } } int main() { int num ; int init_seed ; cin >> num >> init_seed; LCG(num, init_seed); return 0; }
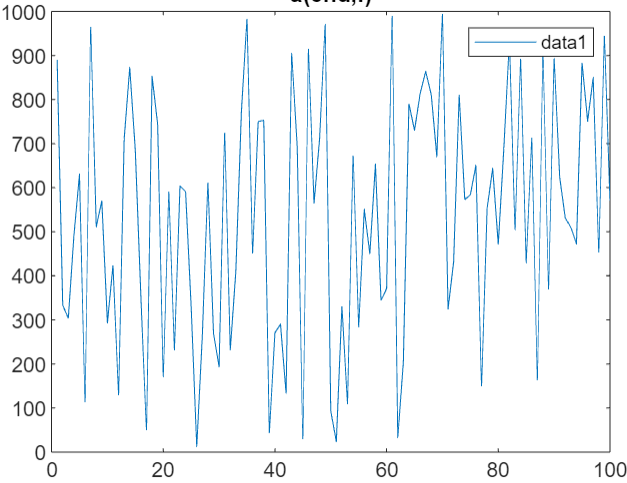
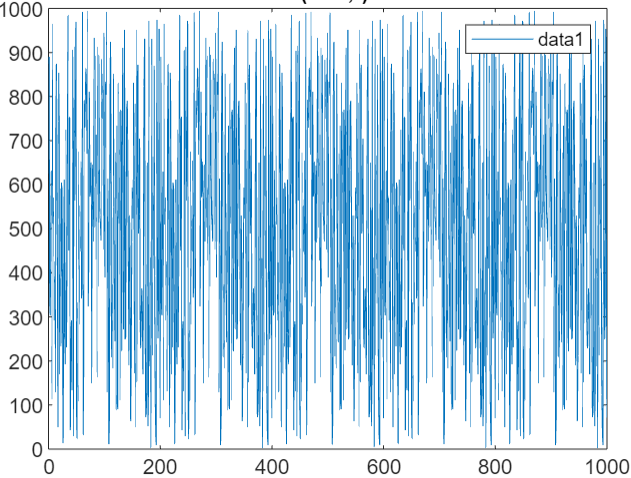
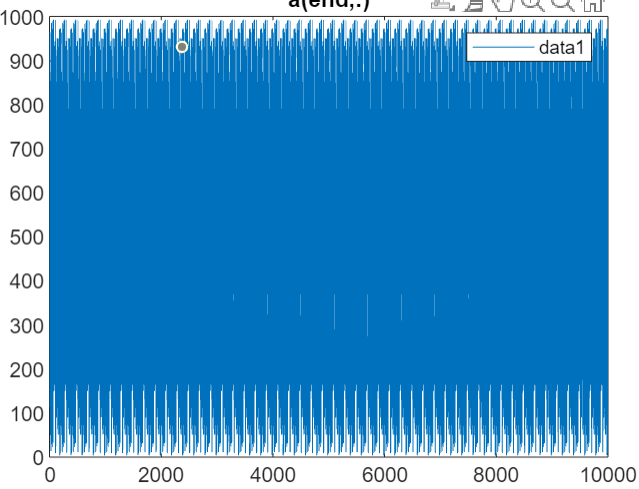
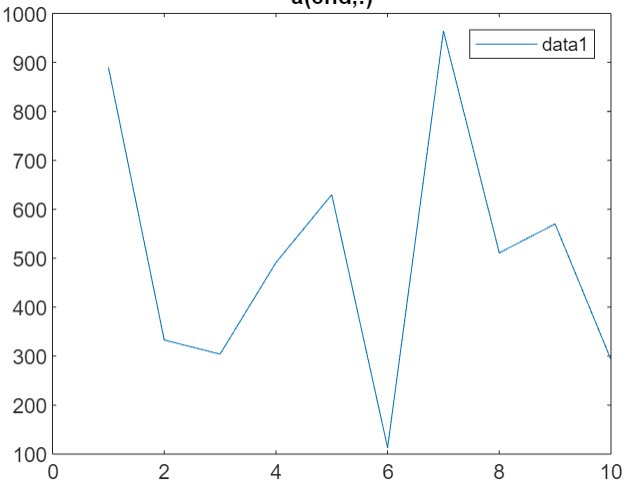
我们固定init_seed的值为71,分别产生10个,100个,1000个和10000个随机数,来观测各自的期望和方差。下图从左至右依次为产生10个,100个,1000个和10000个随机数的数值折线图。
| 期望E(X) | 方差D(X) | |
| 10 | 509.9000 | 268.1917 |
| 100 | 534.5000 | 277.1268 |
| 1000 | 499.5000 | 288.7813 |
| 10000 | 499.5000 | 288.6513 |
通过分析我们可以知道产生的随机数越多,其期望越接近0.5,方差也是比较大的。LCG的优点在于实现比较简单,而且速度比较快,缺点在于其周期只能到232,所以无法实现高质量随机数的应用,从下图可以看出,在初始值inital_seed为71且周期为1000的条件下,从200个数之后就已经开始重复了,这也是为什么1000个和10000个随机数期望相同的原因。而且LCG对于A,C,M的值的选取有一定的要求。
数值概率算法
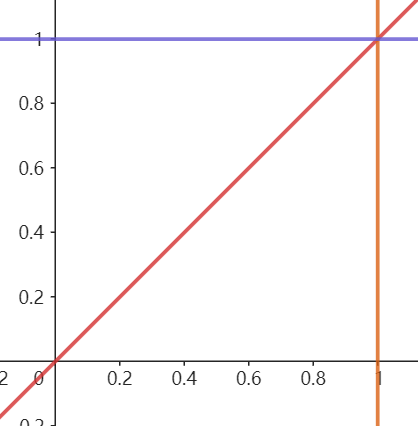
数值概率算法指通过概率计算的方式来得到具体问题的近似解。如通过数值概率算法来求解定积分$\int_{a}^{b}f(x)\text{d}x$。其中定积分$\int_{a}^{b}f(x)\text{d}x$,f(x)>0的几何意义是由直线x=a,x=b,y=0(x轴),y=f(x)所围成的曲边梯形的面积。
使用数值概率算法求解$\int_{0}^{1}x\text{d}x$的值。其中,积分的值为下三角形所围成的面积。在整个方形区域内随机产生诸多的点,看最后落在下三角中点的个数与整个点数的比值就是该积分的值。
#include<iostream> #include<cstdlib> #include<ctime> using namespace std; #define num 100000 int main(){ long int a[num]={0}; long int b[num]={0}; long int count =0; srand((int)time(0)); for(int i = 0; i < num; i++){ a[i] = (double)(rand()%num);//由于随机数产生只能是整数,通过这种方式等比例缩小到[0,1]之内。 b[i] = (double)(rand()%num); if(a[i] > b[i]) count++; //计算落在积分区域内点的数目 } cout <<endl << (double)count/num; return 0; }
其中,num的值用于产生在方形区域内点的数目,我们已知$\int_{0}^{1}x\text{d}x$的值是0.5,通过下表可知,当产生点的数目越多,其解的精确性也就越高。当然缺点也很明显,无论怎样扩大点的数目,最终的结果都只是近似解。
| num\次数 | 1 | 2 | 3 | 4 | 5 |
| 100 | 0.49000 | 0.42000 | 0.43000 | 0.47000 | 0.49000 |
| 1000 | 0.48800 | 0.48400 | 0.50700 | 0.50500 | 0.50000 |
| 10000 | 0.49580 | 0.49040 | 0.50380 | 0.49830 | 0.50760 |
| 100000 | 0.50086 | 0.49985 | 0.50054 | 0.49933 | 0.49980 |
舍伍德算法(sherwood algorithm)
为了能够更好的理解舍伍德算法,在正式介绍舍伍德算法之前,首先我们讨论一个经典的排序算法,快速排序。
快速排序
快速排序于1962年被提出,几十年过去,仍然是极为经典的内部排序算法之一。快速排序是主要思想是:1) 首先选择待排数组中的一个数作为基准;2) 将数组依次左右遍历,使得基准数左边的数均小于(或大于)它,右边的数均大于(或小于)它;3) 最后在左右两个区间中不断重复,直到每个区间就剩一个数。快速排序的最好时间复杂度和平均时间复杂度均为O(nlg n),最坏的时间复杂度为O(n2)。而最坏情况产生往往是在待排数据基本有序的情况下,才会产生。所以如果能够将待排数据基本有序的情况变得不有序,那么快排的效率就会变得更高。
无论自然界、人类社会,抑或浩瀚宇宙,一切事物从整体上都在向着无序化迈进。
舍伍德算法
如果在快速排序进行挑选基准元素时随机,或者在挑选基准元素之后将待排元素数组打乱,这样就保证了算法线性时间的平均性能,就能够产生更好的效率。随机选择一个基准元素比较简单,所以如何将一个数组随机打乱,将是接下来讨论的重点。
洗牌算法
假设给定一个长度为n的数组,现在要求随机打乱。其实这个问题就是包含了两个点:1) 什么才是真的乱?2) 如何实现?随机打乱一个长度为n数组,类似于将该数组重新随机放进另外一个数组中去,第一个元素有n种放法,第二个元素有n-1种放法,… ,所以一共有n!种方法,也就是n!种打乱的方法,所以一个合格是洗牌算法对于一个确定的数组理论上应该产生n!种结果。本次介绍的洗牌算法参照Knuth-Durstenfeld Shuffle算法,其原理是首先随机产生一个0-n-1中的随机数作为待交换元素的下标,然后和最后一个元素交换,之后随机产生一个0-n-2中的随机数作为待交换元素的下标,然后和倒数第二个元素交换,以此类推。我们可以分析出来,该算法的生成结果有n!种,满足一个合格洗牌算法的要求。
#include <iostream> #include<cstdlib> #include<ctime> using namespace std; #define num_element 10 void swap(int a[], int i, int j) { int temp = 0; temp = a[i]; a[i] = a[j]; a[j] = temp; } int main() { int X = 0, j = 0; int array[num_element] = {1,2,3,4,5,6,7,8,9,10}; for (int i = 0; i < num_element -1; i++) { srand((int)time(NULL)); //产生随机种子 X = rand() % (num_element - j) + 1; //产生需要交换的第几个元素 swap(array, X-1, num_element - j-1); j++; } while (j >= 0) { cout << array[j] << endl; j--; } return 0; }
蒙特卡罗算法
k)。所以我们将通过主元素问题来学习蒙特卡罗算法。
主元素问题
在一个数组中,如果某个元素出现的次数超过了该数组长度的一半,则该元素称之为该数组的主元素。现在有一个长度为n的数组,如何找出其中的主元素。首先能够想到的方法就是做一个循环,从左至右依次选择数据进行判断比较,这种方法简单有效,而且能够给出准确的答案,究竟是有还是没有。另外一种方法是利用蒙特卡罗算法来随机选择一个元素,然后进行比较,由于是随机选择元素,所以如果返回没有主元素,是没有办法判断数组中是否真的有没有主元素。不过可以通过反复调用该算法来提高准确性。
#include<iostream> #include<ctime> #include<cstdlib> using namespace std; int master_element(int array[], int length) { srand(time(NULL)); int i = rand() % (length - 1) ; int X = array[i]; int count = 0; for (int j = 0; j < length; j++) { if (array[j] == X) count++; } if (count > length / 2) return X; else return 10000; } int main() { int A[] = { 1,2,3,4,5,5,5,5,5,5,5,7 }; master_element(A, 12); return 0; }
拉斯维加斯算法
拉斯维加斯算法若返回出了解,则这个解一定是最优解,但是拉斯维加斯算法却不一定能够找到解。所以一般情况下,通常用一个布尔型方法来表示拉斯维加斯算法,当没有找到解时,可以再一次调用算法来使得算法的成功率提高。
总结
概率算法更多的是一种思想,对于某一种问题,不一定要使用概率算法来进行求解。比如主元素问题,选定元素依次遍历可以解决,使用散列表也能够解决。在无法使用确定性算法得到解或者得到解的代价太大,而恰恰对于解的误差可以接受时,概率算法的确是一种不错的选择。毕竟有些问题还是很依赖概率的。
参考资料
[1] 概率算法,百度百科,https://baike.baidu.com/
[2] 王晓东.算法设计与分析(第3版)[M].北京:清华大学出版社,2014:190-214.
[3] 线性同余法,CSDN,https://blog.csdn.net/fengying2016/article/details/80573287
[4] 线性同余方法(LCG)产生随机数,知乎,https://zhuanlan.zhihu.com/p/71583737
今天的文章【算法学习】- 概率算法分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/54124.html