蒙特卡洛(Monte Carlo)方法,又称随机抽样或统计试验方法,是以概率和统计理论方法为基础的一种计算方法。该方法使用随机数(或更常见的伪随机数)来解决很多计算问题,将所求解的问题同一定的概率模型相联系,用电子计算机实现模拟或抽样,以获得问题的近似解。
基本原理
蒙特卡罗方法通过抓住事物运动的几何数量和几何特征,利用数学方法来加以模拟,即进行一种数字模拟实验。它以一个概率模型为基础,按照这个模型所描绘的过程,通过模拟实验的结果,作为问题的近似解。蒙特卡罗解题可归结为三个主要步骤。
- 构造或描述概率过程
- 实现从已知概率分布抽样
- 建立各种评估量
借助计算机技术,蒙特卡罗模拟实现了两大优点:
简单,省却了繁杂的数学报导和演算过程,使得一般人能够理解和掌握
快速,简单和快速
蒙特卡罗模拟的特点:随机采样上计算得到近似结果,随着采样的增加,得到的结果是正确的结果的概率逐渐增大。
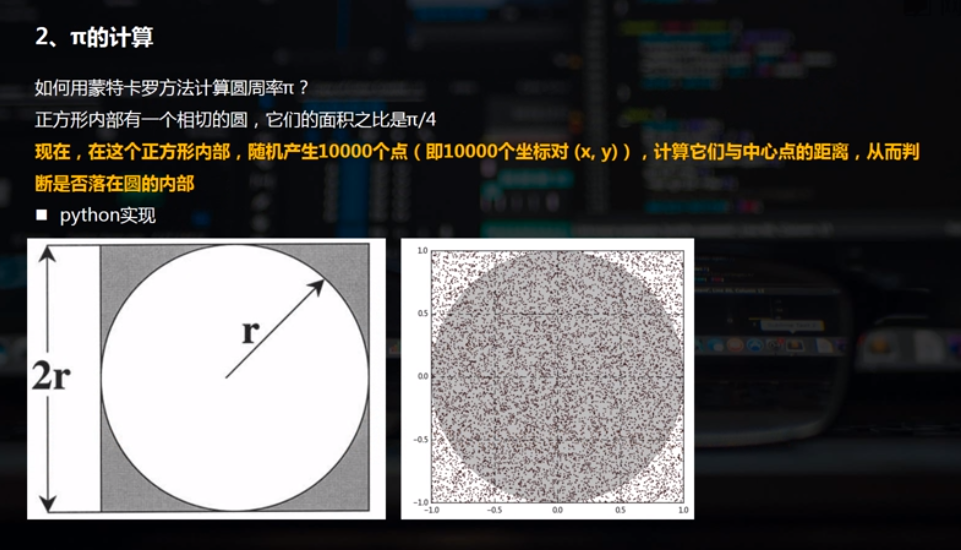
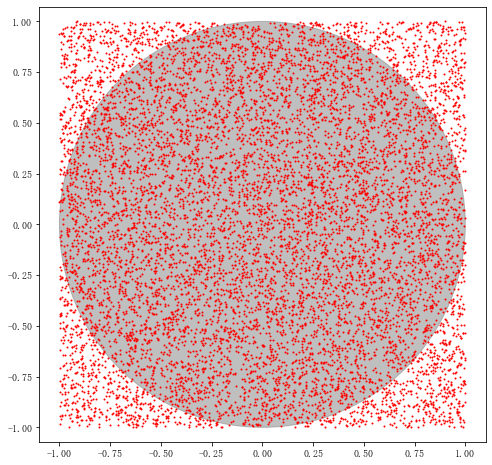
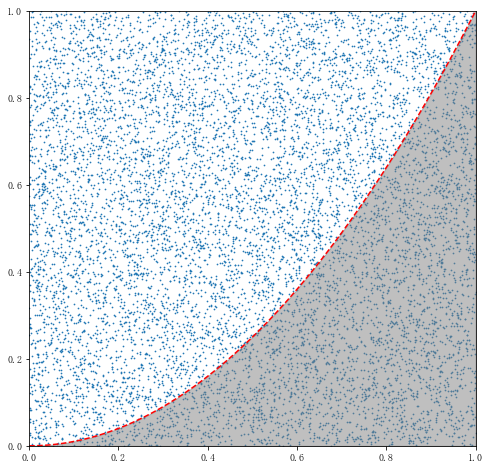
1.π的计算
n = 10000 r = 1.0 a,b = 0.0,0.0 xmin,xmax = a-r,a+r ymin,ymax = b-r,b+r x = np.random.uniform(xmin,xmax,n) #均匀生成介于xmin和xmax的n个值 y = np.random.uniform(ymin,ymax,n) fig = plt.figure(figsize = (8,8)) ax = fig.add_subplot(111) plt.plot(x,y,'ro',markersize = 1) #散点图,也即plt.scatter(x,y,s=1) plt.axis('equal') from matplotlib.patches import Circle circle = Circle(xy=(a,b),radius=r,alpha = 0.5,color = 'gray') #xy表示圆心位置,radius表示半径 ax.add_patch(circle) d = np.sqrt((x-a)**2+(y-b)**2) #求点到圆心的距离 m = len(d[d < r]) #落在圆内的点的个数 #圆的面积/正方形面积=π*(r**2)/(2r)**2 = π/4 = 圆内的点的个数/总个数 = m/n π = 4*m/n print(π) # 3.1388
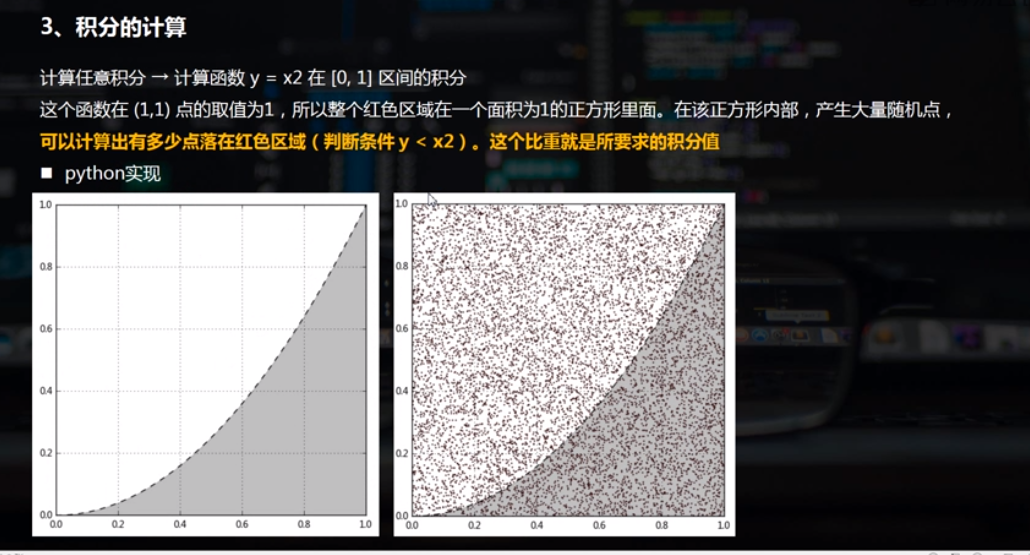
2.积分的计算
n = 10000 xmin,xmax = 0,1.0 #矩形x轴边界 ymin,ymax = 0,1.0 #矩形y轴边界 x = np.random.uniform(xmin,xmax,n) y = np.random.uniform(ymin,ymax,n) fig = plt.figure(figsize = (8,8)) ax = fig.add_subplot(111) plt.scatter(x,y,s=0.5) #在矩形内随机投点 plt.xlim([0,1]) plt.ylim([0,1]) xi = np.linspace(0,1,100) yi = xi**2 plt.plot(xi,yi,linestyle='--',color = 'red') #绘制y = x**2曲线 plt.fill_between(xi,yi,0,color='gray',alpha=0.5) #填充y<x**2部分 m = len(d[y<x**2]) #求落在阴影部分的点的个数 integral = m/n #阴影部分点的个数/总个数 print(integral) #0.3326
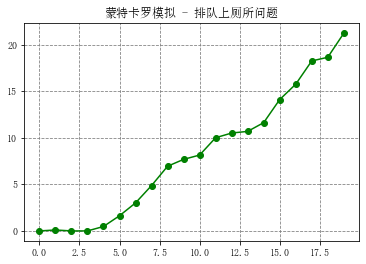
3.排队上厕所问题
# 1.两场电影结束时间相隔较长,互不影响; # 2.每场电影结束之后会有20个人想上厕所; # 3.这20个人会在0到10分钟之内全部到达厕所); # 4.每个人上厕所时间在1-3分钟之间 # 首先模拟最简单的情况,也就是厕所只有一个位置,不考虑两人共用的情况则每人必须等上一人出恭完毕方可进行。 # 分析:对于每个人都有几个参数:到达时间 / 等待时间 / 开始上厕所时间 / 上厕所时间 / 结束时间 arrivingtime = np.random.uniform(0,10,20) #到达时间 arrivingtime.sort() workingtime = np.random.uniform(0,3,20) #上厕所时间 startingtime = [0 for i in range(20)] #开始时间 waitingtime = [0 for i in range(20)] #等待时间 finishingtime = [0 for i in range(20)] #完成时间 emptytime = [0 for i in range(20)] #厕所空闲时间 startingtime[0] = arrivingtime[0] #第一个人开始时间等于到达时间 finishingtime[0] = startingtime[0] + workingtime[0] #第一个人结束时间等于开始时间+上厕所时间 waitingtime[0] = startingtime[0] - arrivingtime[0] print(arrivingtime[0],waitingtime[0],startingtime[0],workingtime[0],finishingtime[0]) print('-------------------------------------') print(' 到达时间 等待时间 开始时间 消耗时间 结束时间 厕所空闲时间') for i in range(len(arrivingtime)-1): if arrivingtime[i+1]<=finishingtime[i]: #如果某个人到达,上一个人尚未结束,则这个人的开始时间为上一个人的结束时间 emptytime[i] = 0 startingtime[i+1] = finishingtime[i] else: emptytime[i] = arrivingtime[i+1] - finishingtime[i] startingtime[i+1] = arrivingtime[i+1] #如果某个人到达,上一个人已结束,则这个人的开始时间即为他的到达时间 waitingtime[i+1] = startingtime[i+1] - arrivingtime[i+1] finishingtime[i+1] = startingtime[i+1]+ workingtime[i+1] for i in range(len(arrivingtime)) : print('第 %d个人:%.5f, %.5f, %.5f, %.5f, %.5f, %.5f'%(i,arrivingtime[i],waitingtime[i],startingtime[i],workingtime[i],finishingtime[i],emptytime[i])) print('平均等待时间为:',np.mean(waitingtime)) fig = plt.figure(figsize = (6,4)) plt.plot(waitingtime, '-go') plt.grid(True,linestyle='--', color = 'gray',linewidth = '0.8') plt.title('蒙特卡罗模拟 - 排队上厕所问题')


0.2736595351122484 0.0 0.2736595351122484 0.38688603398898835 0.6605455691012367 ------------------------------------- 到达时间 等待时间 开始时间 消耗时间 结束时间 厕所空闲时间 第 0个人:0.27366, 0.00000, 0.27366, 0.38689, 0.66055, 0.00000 第 1个人:0.56116, 0.09938, 0.66055, 0.43453, 1.09507, 0.35845 第 2个人:1.45352, 0.00000, 1.45352, 0.21734, 1.67086, 0.56067 第 3个人:2.23153, 0.00000, 2.23153, 0.69145, 2.92298, 0.00000 第 4个人:2.44763, 0.47535, 2.92298, 1.53950, 4.46249, 0.00000 第 5个人:2.83300, 1.62948, 4.46249, 2.88175, 7.34424, 0.00000 第 6个人:4.33856, 3.00568, 7.34424, 1.86335, 9.20758, 0.00000 第 7个人:4.34006, 4.86752, 9.20758, 2.33044, 11.53803, 0.00000 第 8个人:4.59969, 6.93834, 11.53803, 0.75576, 12.29379, 0.00000 第 9个人:4.61749, 7.67631, 12.29379, 0.59378, 12.88758, 0.00000 第 10个人:4.74960, 8.13797, 12.88758, 2.01128, 14.89885, 0.00000 第 11个人:4.89969, 9.99916, 14.89885, 0.67834, 15.57720, 0.00000 第 12个人:5.07639, 10.50081, 15.57720, 1.03112, 16.60832, 0.00000 第 13个人:5.93106, 10.67725, 16.60832, 2.04646, 18.65478, 0.00000 第 14个人:7.03743, 11.61735, 18.65478, 2.48112, 21.13590, 0.00000 第 15个人:7.04236, 14.09354, 21.13590, 2.99854, 24.13444, 0.00000 第 16个人:8.39554, 15.73890, 24.13444, 2.72812, 26.86256, 0.00000 第 17个人:8.62632, 18.23625, 26.86256, 0.46716, 27.32973, 0.00000 第 18个人:8.70150, 18.62823, 27.32973, 2.67838, 30.00811, 0.00000 第 19个人:8.80044, 21.20767, 30.00811, 0.67289, 30.68100, 0.00000 平均等待时间为: 8.176459882353335
输出结果
今天的文章蒙特卡洛算法分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/55710.html