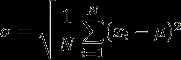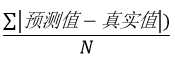均方根误差和标准误差_方差与标准差的均方误差谁大

单纯介绍概念不易理解，所以应从实际应用出发介绍其区别。四者的不同可从研究对象和研究目的进行区分。

一 区别比较

1. 方差
   定义：方差在统计描述和概率分布中各有不同的定义，并有不同的公式。
   （1）统计学
   统计学中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。
   （2）概率论
   度量随机变量和其数学期望（即均值）之间的偏离程度。
   来源：
   离均差：即一个样本中的数据与均值之差。将离均差进行改进得到了方差。
   。。。
   补充：
   离均差又是从极差发展而来的。
   极差是最大值－最小值，最初用极差来评价一组数据的离散度。
   因为由两个数据来评判一组数据是不科学的，所以从极差进行改进，改用离均差之和。
   使用离均差不好吗？为什么又设置方差：
   （1）为避免出现离均差总和为零，所以对离均差求平方。
   （2）而为避免离均差平方和受样本含量的影响，所以对离均差平方和除以样本数，求平均值。
   这样就得到了方差。
   公式：
   （1）统计学
   针对总体数据的公式，其中N是总体数据的数量：
   
   为总体方差， 为变量， 为总体均值， 为总体数据数量。
   针对样本抽样的公式（日常工作中用）：
   S^2= ∑(X- ) ^2 / (n-1)
   实际工作中，总体均数难以得到时，应用样本统计量（即样本数量）代替总体参数，经校正后，样本方差计算公式如上。除以n-1的原因见自由度（为什么样本方差自由度是n-1）_张之海_CSDN
   其中S^2为样本方差，X为变量，为样本均值，n为样本例数。
   （2）概率论
   离散型随机变量：
   D(X)=E{[X-E(X)]^2}=E(X2) – [ E(X)]^2
   连续型随机变量：
   定义域为(a,b)，概率密度函数为f(x)，连续型随机变量X方差计算公式：
   D(X)= (x-μ)^2 f(x) dx
   意义：
   当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小。

2. 标准差(std —— Standard Deviation)
   别名：均方差（mean square error）、标准偏差、实验标准差。
   定义：标准差是观测值与其平均数偏差的平方和的平方根，即方差的算术平方根。
   公式:
   
   公式意义：所有数减去其平均值的平方和，所得结果除以该组数之个数（或个数减一)，再把所得值开根号，所得之数就是这组数据的标准差。
   注意：如是总体，标准差公式根号内除以N。如是样本，标准差公式根号内除以（N-1) 。因为我们大量接触的是样本，所以普遍使用根号内除以（N-1)。
   理论意义：
   （1）标准差反映组内个体间的离散程度。
   （2）描述一组数值自平均值分散开来的程度。一个较大的标准差，代表大部分的数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。
   （3）标准差越高,表示实验数据越离散,也就是说越不精确。标准差越低,代表实验的数据越精确。
   实际应用：
   标准差应用于投资上，可作为量度回报稳定性的指标。标准差数值越大，代表回报远离过去平均数值，回报较不稳定故风险越高。相反，标准差数值越细，代表回报较为稳定，风险亦较小。
   方差、标准差的关系与异同：
   （1）两者的关系
   样本中各数据与样本平均数的差的平方和的平均数叫做样本方差；样本方差的算术平方根叫做样本标准差。
   （2）相同点
   两者都是描述一组（协方差描述两组数据，参考[4]）数据的离散程度的。样本方差或样本标准差越大，样本数据的离散程度就越大。
   （3）不同点
   方差与我们要处理的数据的量纲是不一致的，虽然能很好的描述数据与均值的偏离程度，但是处理结果是不符合我们的直观思维的。
   标准差与方差不同的是，标准差和变量的计算单位相同，比方差清楚，因此很多时候我们分析的时候更多的使用的是标准差。
   标准差和均值的量纲（单位）是一致的，在描述一个波动范围时标准差比方差更方便。比如一个班男生的平均身高是170cm,标准差是10cm,那么方差就是10cm^2。可以进行的比较简便的描述是本班男生身高分布是170±10cm，方差就无法做到这点。

3. 协方差
   用途：衡量两个变量的总体误差。
   .
   与方差、标准差的不同：协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
   .
   公式：
   
   
   从公式中可以看出，协方差是各随机变量与其均数离差之积的均值；如果我们把随机变量与其均数的差值成为“均值化“的随机变量，这么这两个均值化的随机变量应该都具有相同的均值就是0；同时如果二者是相互独立的，那么当X大于其均值的情况下Y应该是有可能大于也有可能小于其均值，这样导致其乘积之和应该为0；也就是说，如果X、Y相互独立，则二者协方差为0。同样可知，如果X、Y线性相关，则其一个大于均值的时候另一个也会大于均值的（因为其均值也是线性相关的）。于是可以看出协方差是判断两个随机变量是否线性相关的很好的物理量。
   特殊情况：
   如果X与Y是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足E[XY]=E[X]E[Y]。
   但是，反过来并不成立。即如果X与Y的协方差为0，二者并不一定是统计独立的。（相关有两种：线性相关、非线性相关。Cov(X,Y)等于0，说明X与Y一定不是线性相关，但是X与Y可能是非线性相关（eg:Y = X^2），这样X与Y仍不是相互独立的。）
   .
   协方差与期望、方差的关系：
   协方差与方差之间有如下关系：
   D(X+Y)=D(X)+D(Y)+2Cov(X，Y)
   D(X-Y)=D(X)+D(Y)-2Cov(X，Y)
   协方差与期望值有如下关系：
   Cov(X，Y)=E(XY)-E(X)E(Y)。
   .
   协方差与pearson系数的关系：
   协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。因此才引入了Pearson相关系数。
   
   若ρXY=0，则X与Y不线性相关。
   即ρXY=0的充分必要条件是Cov(X，Y)=0，亦即不相关和协方差为零是等价的。
   设ρXY是随机变量X和Y的相关系数，则有
   （1）∣ρXY∣≤1；
   （2）∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）

4. 均方根误差(rmse —— root-mean-square error)
   别名:标准误差、均方根差。
   定义：观测值与真值偏差的平方和，与观测次数n比值的平方根。
   公式：
   （1）表示1：√[∑(di^2)/n]
   （2）表示2：S={[(x1-x’1)^2+(x2-x’2)2+…(xn-x’n)^2]/n}0.5（x’1、x’2…x’n为真实值，n为样本个数）
   理论意义：衡量观测值同真值之间的偏差。
   实际用途：衡量测量精度。
   实际应用：标准误差 对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。

5. 平均绝对误差(MAE)
   别名：平均绝对离差
   定义：所有单个观测值与算术平均值的偏差，的绝对值，的平均。
   公式：
   理论意义：平均绝对误差可以避免偏差相互抵消的问题。
   实际用途：描述数据离散程度。

二 离散度形容指标发展历史

极差、方差和标准差等都是形容离散度的指标。
离散度
　　标准差是反应一组数据离散程度最常用的一种量化形式，是表示精密确的最要指标。说起标准差首先得搞清楚它出现的目的。我们使用方法去检测它，但检测方法总是有误差的，所以检测值并不是其真实值。检测值与真实值之间的差距就是评价检测方法最有决定性的指标。但是真实值是多少，不得而知。因此怎样量化检测方法的准确性就成了难题。这也是临床工作质控的目的：保证每批实验结果的准确可靠。 　　
　　虽然样本的真实值是不可能知道的，但是每个样本总是会有一个真实值的，不管它究竟是多少。可以想象，一个好的检测方法，其检测值应该很紧密的分散在真实值周围。如果不紧密，那距真实值的就会大，准确性当然也就不好了，不可能想象离散度大的方法，会测出准确的结果。因此，离散度是评价方法的好坏的最重要也是最基本的指标。 　　
　　一组数据怎样去评价和量化它的离散度呢?人们使用了很多种方法：
极差
　　最直接也是最简单的方法，即最大值－最小值（也就是极差）来评价一组数据的离散度。这一方法在日常生活中最为常见，比如比赛中去掉最高最低分就是极差的具体应用。
离均差的平方和
　　由于误差的不可控性，因此只由两个数据来评判一组数据是不科学的。所以人们在要求更高的领域不使用极差来评判。其实，离散度就是数据偏离平均值的程度。因此将数据与均值之差（我们叫它离均差）加起来就能反映出一个准确的离散程度。和越大离散度也就越大。 　　但是由于偶然误差是成正态分布的，离均差有正有负，对于大样本离均差的代数和为零的。为了避免正负问题，在数学有上有两种方法：一种是取绝对值，也就是常说的离均差绝对值之和。而为了避免符号问题，数学上最常用的是另一种方法－－平方，这样就都成了非负数。因此，离均差的平方和成了评价离散度一个指标。　　
方差（S2）
　　由于离均差的平方和与样本个数有关，只能反应相同个数样本的离散度，而实际工作中做比较很难做到样本的个数相同，因此为了消除样本个数的影响，增加可比性，将标准差求平均值，这就是我们所说的方差成了评价离散度的较好标准。 　　
　　样本量越大越能反映真实的情况，而算数均值却完全忽略了这个问题，对此统计学上早有考虑，在统计学中样本的方差多是除以自由度（n-1)，它是意思是样本能自由选择的程度。当选到只剩一个时，它不可能再有自由了，所以自由度是n-1。为什么除以n-1呢？请参考：自由度（为什么样本方差自由度是n-1）_张之海_CSDN

##参考文献：
[1] 均方根误差与标准差 — 新浪博客
[2] 均方根误差 — 百度百科
[3] 标准误差standard error,均方根误差/中误差（RMSE,root mean squared error）— 新浪博客
[4] 方差、标准差和协方差三者之间的定义与计算—寻自己—博客园
[5] 方差—百度百科
[6]方差、标准差、均方差、均方误差区别总结
[7] 协方差_百度百科

今天的文章均方根误差和标准误差_方差与标准差的均方误差谁大分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。