弗洛伊德算法例题图解_floyd算法可以有负权

floyd算法用来求解图中任意两点之间的最短距离，主要思路是暴力求解任意两点之间的最短距离，使用三层循环遍历节点，第一层循环表示中间节点k，第二、三层循环表示表示i到j之间的最短距离，我们在遍历的时候维护顶点i到j的最短记录即可。每一次判断是否存在中间节点k使得顶点i到j的距离更短，如果更短那么就更新i到j的最短距离。
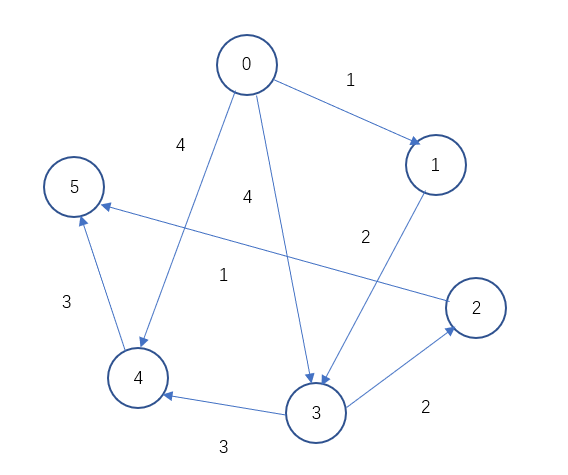
下面是具体的有向有权图的例子：

测试数据：

6 8
0 1 1
0 4 4
0 3 4
1 3 2
2 5 1
3 2 2
3 4 3
4 5 3

代码如下：

import sys


def floyd():
    # n为顶点数目, e为边的数目
    n, e = map(int, input().split())
    # 距离列表用来记录任意两点之间的最短距离
    dis = [[sys.maxsize] * n for i in range(n)]
    # 有向有权图
    for i in range(e):
        # a->b的距离为c
        a, b, c = map(int, input().split())
        dis[a][b] = c
    # 自己到自己的距离是0
    for i in range(n):
        dis[i][i] = 0
    # 三层循环第一层循环表示中间节点k, 第二,三循环表示从i到j的距离最短距离
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if dis[i][k] != sys.maxsize and dis[k][j] != sys.maxsize and dis[i][j] > dis[i][k] + dis[k][j]:
                    dis[i][j] = dis[i][k] + dis[k][j]
    return dis


if __name__ == '__main__':
    dis = floyd()
    n = len(dis)
    for i in range(n):
        print(dis[i])

今天的文章弗洛伊德算法例题图解_floyd算法可以有负权分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。