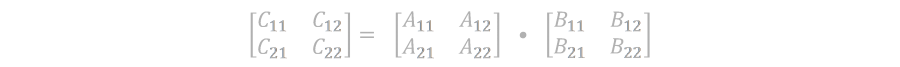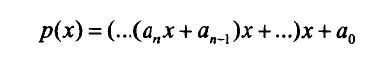好久不见,这里依旧是代班的工人~
可能不是很想。。。emmm。。。没关系。。。
最近越学越发觉自己懂得好少。。。
但是最近又好忙好忙。。。
不过如今你们看到了这篇文章,说明我还是挺过来了!鼓掌~
(虽然不知道能不能挺过下周)
那么,趁着我还活着,这次还是带来基础算法的知识
秉持着大神来回顾,小白来学习的原则
让我们开始这期的学习吧!
目录
01.减治法
02.分治法
03.变治法
01
减 治 法
decrease-and-conquer method
普卢塔克说,萨特斯为了告诉他的士兵坚忍和智慧比蛮力更重要的道理,把两匹马带到他们面前,然后让两个人拔光马的尾毛。一个人是魁梧的大力士,他用力地拔了又拔,但一点效果也没有;另一个人是一个精美的、长相矫捷的裁缝,他微笑着,每次拔掉一根毛,很快就把尾巴拔得光秃秃的。
——E. Cobham Brewer,《惯用语和寓言词典》,1898
减治法(decrease-and-conquer method)
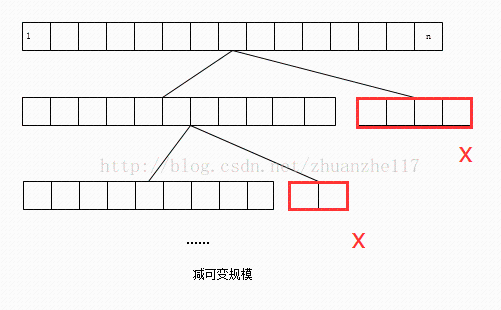
减治法采取划分后选择计算的思想,利用一个问题和同样较小规模的问题之间的某种关系进行划分。我们先确立这种关系,然后既可以从顶至下,也可以从底至上地来运用该关系,将大问题分解成小问题来解决,像是层层嵌套。在实际解决的过程中只针对部分子问题进行求解。
减治法有3种主要的变种:
1.减去一个常量 (decrease by a constant)
2.减去一个常数因子(decrease by a constant factor)
3.减去的规模是可变的(variable size decrease)
1.减去一个常量 (decrease by a constant)
在减常量变种中,我们每次从问题规模中减去一个规模相同的常量。(一般来说,这个常量等于一)
(CSDN盗图,别介意~)
函数f(n) = a^n的求解过程就是一个栗子:
在这里,虽然算法的时间复杂度和蛮力法一致,但是体现的思想却不一样。
其他的栗子还有:
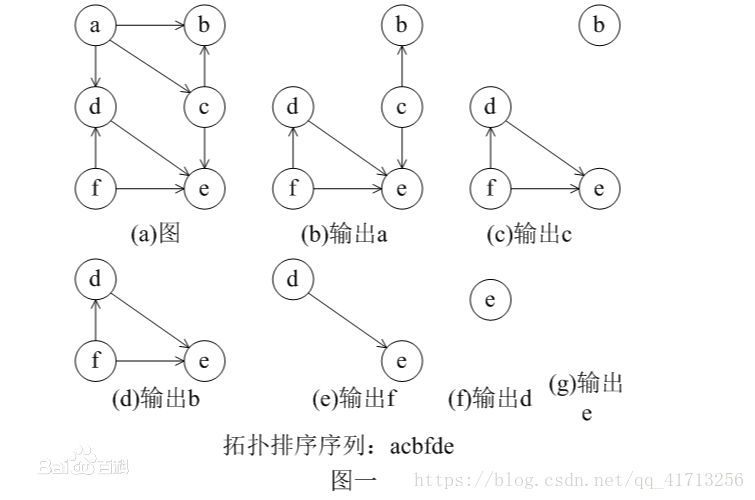
深度优先、广度优先查找,拓扑排序等。这里对拓扑排序稍加介绍。
拓扑排序是指:对一个有向无环图G进行排序,将G中所有顶点排成一个一维线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前(起点在终点之前)。
运用减治法思想的步骤:
1.在有向图中选一个没有前驱的顶点,输出;
2.删除所有和它有关的边;
3.重复上述两步,直至所有顶点输出。
(每次我们只减去常量1,因此当有多个点没有前驱时,只需要随意挑选一个点输出)
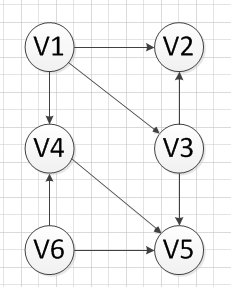
比如这样一个图:
再比如这样一个图(其实是同一个图啦):
我们最终会得到这样的序列:
v6—>v1—>v4—>v3—>v5—>v2;
当然,类似这样的序列也是正确的:
v1—>v6—>v4—>v3—>v5—>v2;
v1—>v3—>v6—>v4—>v5—>v2。。。
这里是要强调选择的随机性。这完全由代码决定。
没什么大问题,下面就到了激动人心的代码环节:
//拓扑排序:寻找图中入度为0的顶点作为即将遍历的顶点,遍历完后,将此顶点从图中删除 #include using namespace std; int adjMatrix[105][105];//参数adjMatrix:邻接矩阵 int source [105]; // 参数source:给出图的每个顶点的入度值 int n,m; //给出图的顶点、边个数 void getSourceSort( ){
int count = 0; //用于计算当前遍历的顶点个数 bool judge = true; while(judge) {
for(int i = 1;i <= n;i++) {
if(source[i] == 0) //当第i个顶点入度为0时,遍历该顶点 { count++; if (count "; if(count==n)cout< source[i] = -1; //代表第i个顶点已被遍历 for(int j = 1;j <= n;j++) //寻找第i个顶点的出度顶点 {
if(adjMatrix[i][j] == 1) source[j] -= 1; //第j个顶点的入度减1 } } } if(count == n) judge = false; } } //返回给出图每个顶点的入度值 void getSource( ){
for(int i = 1;i <= n;i++) //若邻接矩阵中第i列含有k个1,则在该列的节点的入度为k,即source[i] = k { int count = 0; for(int j = 1;j <= n;j++) {
if(adjMatrix[j][i] == 1) count++; } source[i] = count; } } int main(){
int a,b; cin>>n>>m; for(int i = 1;i <= n;i++) //初始化邻接矩阵 for(int j = 1;j <= n;j++) adjMatrix[i][j] =0; for(int i = 1;i <= m;i++) {
cin>>a>>b; adjMatrix[a][b] = 1; } getSource(); getSourceSort( ); return 0;}2.减去一个常数因子(decrease by a constant factor)
减去常数因子实际上就是把规模除以一个常数。(在多数情况下,这个常数因子是二)
继续以计算f(n)=a^n为栗:

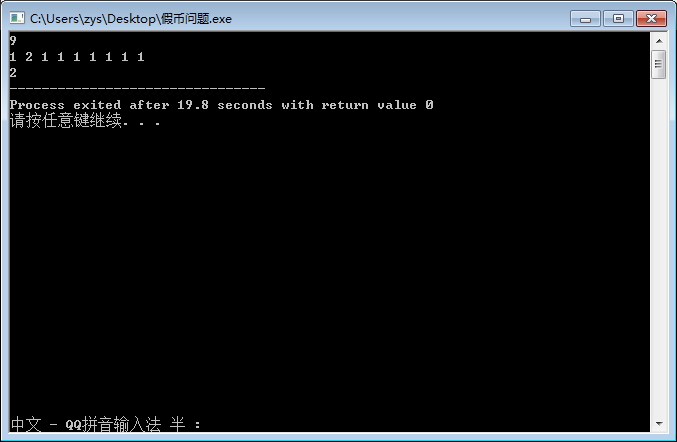
对分查找,假币问题都可以用这种思想。我们以假币问题为例:
有n枚银币,其中有1枚是假的,假币重量偏重、偏轻未知,输入银币的重量,求假币的位置。
我们先取出一枚银币作为对照,再将银币分为两半称重,每次称重对比,再从有问题的一堆中继续称重查找。这样,每次我们都减去了常量因子2。
当然,银币总数是奇偶时需要不同的处理方式,在银币数量为偶数时,由于不知道假币偏轻或偏重,我们需要选择一个compare进行对照。
同时,我们还可以把银币分为三堆考虑,进一步优化时间复杂度。(作为代价,代码要考虑总数mode3余1、2、0的情况,同时要比较三堆,会稍稍复杂一些)
Codding time:
//三分法求八枚银币问题#include using namespace std;int coin[105],num;int sum(int left, int right){
int sum = 0; for (int i = left; i <= right; i++) sum += coin[i]; return sum;}int findfake(int left, int right){
int n=right-left+1; int p1=(right+left)/3; int p2=p1*2; int sign = n % 3; if (sign == 0) {
int fake = 0; int A, B, C; A = sum(left,p1); B = sum(p1+1,p2); C = sum(p2+1,right); if (n == 3) {
if (A == B) {
fake = right; } else if (A == C) {
fake = right - 1; } else {
fake = left; } return fake; } else {
if (A == B) {
fake = findfake(p2+1,right); return fake; } else if (A == C) {
fake = findfake(p1+1,p2); return fake; } else {
fake = findfake(left,p1); return fake; } } } if (sign == 1) {
int fake = right; int A, B, C; A = sum(left,p1); B = sum(p1+1,p2); C = sum(p2+1,right-1); if (n == 1) {
return fake; } else {
if (A == B) {
if (A == C) return fake; if (A !=C) {
fake = findfake(p2+1,right-1); return fake; } } else if (A == C) {
fake = findfake(p1+1,p2); return fake; } else {
fake = findfake(left,p1); return fake; } } } if (sign == 2) {
int fake = 0; int x1 = right - 1; int x2=right; int A, B, C; A = sum(left,p1); B = sum(p1+1,p2); C = sum(p2+1,right-2); if (n == 2) {
int campare; //参照物 if (right != num) campare = coin[num]; else campare = coin[1]; if (coin[x2] == campare) fake = x1; else fake = x2; return fake; } else {
if (A == B && B == C) {
int campare = coin[0]; if (coin[x1] == campare) fake = x2; else fake = x1; return fake; } else if ((A == B) && (A!=C)) {
fake=findfake(p2+1,x1-1); return fake; } else if (A == C) {
fake=findfake(p1+1,p2); return fake; } else {
fake = findfake(left,p1); return fake; } } } return 0;}int main(){
cin >> num; for (int i = 1; i <= num; i++) cin >> coin[i]; int fake=findfake(1,num); cout << fake; return 0;}3.减去的规模是可变的(variable size decrease)
字面理解,就是指每次减去的规模的模式或数值是不同的。
这里我们拿欧几里德算法为栗子。学过数论的盆友们知道(数学害人不浅啊),欧几里得算法是一种求最大公约数的较为简便的方法,也叫辗转相除法。用一个简单的式子来表示:
gcd(a,b) = gcd(b,a mod b) (这里a>b)
(题外话,我记得数论里最大公约数是不需要gcd的。。。)
可以大致想象到,这里每次减去的规模是完全未知、可变的。
我们再举一个栗子:二叉查找树。
百度百科告诉我们,二叉查找树是一颗这样的树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
(4)没有键值相等的结点。
根据树的性质,我们可以发现对二叉查找树的查找并不困难,只要从顶点开始不断比较就行了。但二叉查找树不一定就是平衡二叉树,如果只有一个分支,那减去的规模就会变化。(为什么我感觉解释的好扯啊。。。)
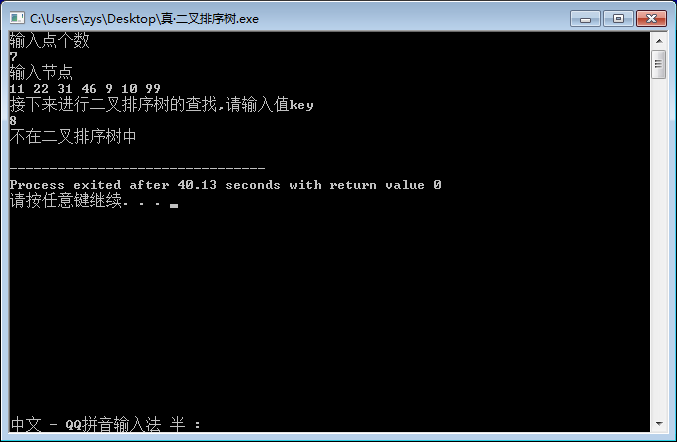
查找的代码并不困难,我们这里只给出实现插入和查找两种功能的代码。
(就当练习数据结构了= =)
Coding time:
//二叉排序树 #include using namespace std;typedef class BiTNode //定义结点类,指针类型名 {
public: int data; class BiTNode *leftchild, *rightchild;}*BiTree; // BST查找,查找成功,则p指向该元素节点,返回truebool searchBST(BiTree T,int key,BiTree f,BiTree &p){
if (!T) {
p = f; return false; } else if (key == T->data) {
p = T; return true; } else if (key < T->data) return searchBST(T->leftchild, key, T, p); else return searchBST(T->rightchild, key, T, p);} //BST插入,用于建立树 bool insertBST(BiTree &T, int key){
BiTree p, s; //因为在searchBST的过程中有进行比较,所以search完T就指向该插入位置的父结点 if (!searchBST(T, key,NULL, p)) {
s = new BiTNode; s->data = key; s->leftchild = s->rightchild = NULL; if (!p) T = s; //p是空的说明树是空的,则插入在根节点 else if(key < p->data) p->leftchild = s; else p->rightchild = s; return true; } else return false;} int main(){
//二叉树的创建 int n; cout<<"输入点个数"<<endl; cin>>n; BiTree T = NULL; cout<<"输入节点"<<endl; for (int i = 0; i < n; i++) {
int a; cin>>a; insertBST(T, a); } //二叉树的查找 BiTree p=NULL; BiTree f=NULL; cout<<"接下来进行二叉排序树的查找,请输入值key"<<endl; int key; cin>>key; if (searchBST(T, key, f, p)) cout<<"在二叉排序树中"<<endl; else cout<<"不在二叉排序树中"<<endl; return 0;}emmm,这图好像看不出什么。。。
编写的过程中有一点小插曲,我看错了树的定义,所以一开始的版本出现了错误(┬_┬),可以放出来给无聊的人看看,找找错。(说明看对题目真的很重要!!!)
wrong code:
//二叉查找树的建立(数组实现) #include using namespace std; int size=0; //size为树的规模 int tree[1005]; const int INF=0;void addElement(int element){
int p = 1; //指标p if(size == 0) {
tree[p] = element; size++; return; } while(true) {
if(element {
int p1 = 2 * p ; //p1指向p的左儿子的位置 if(tree[p1] == INF) {
tree[p1] = element; size++; return; } else p = p1; } else {
int p2 = 2 * p + 1; //p2指向p的右儿子的位置 if(tree[p2] == INF) {
tree[p2] = element; size++; return; } else p = p2; } }} int main(){
int i,j=1; for (i=1;i<=size;i++) tree[i]=INF; int temp; while(cin>>temp) {
addElement(temp); } for (i=1;j<=size;i++) {
if(tree[i]!=INF) {
cout<" "; j++; } } return 0;}02
分 治 法
divide-and-conquer algorithm
无论人们在祈祷什么,他们总是在祈祷一个奇迹。每一个祈祷都可以简化为:伟大的上帝呀,请让两个二相加不等于四吧。
——伊万·屠格涅夫(1818 - 1883),俄国作家和短篇小说家
关于分治法,本公司的另一位老板在一年前也写过啦(老板真强,老板真强。。。),大家可以看看那篇,很详细(不是说讲解详细):
经典优化算法之分治法(Divide-and-Conque Algorithm)
转载 |【算法】分治法(Divide-and-Conquer Algorithm)经典例子分析
从字面上分析就可以看到有哪些步骤:
分-分解-将问题分解为规模更小的子问题,子问题最好相同或相似;
治-求解-将这些规模更小的子问题逐个击破;
合-合并-将已解决的子问题合并,最终得出原问题的解;
(有时原始问题的解只存在于分解出的某一个(或某几个)子问题中,则只需要在这一(或这几个)子问题中求解即可。例如在图书馆里找书。)
从上述步骤中我们可以看出,分治算法一般适用满足以下条件的场景:
1)问题规模缩小到一定的程度就可以很容易解决;
2)问题可以分解为若干个规模较小的相同问题;
3)问题分解出的若干子问题的解可以合并为该问题的解;
4)每个子问题都是独立的,相互之间没有交集。(这是区别分治法与减)
在“分”的过程中,我们尽可能让分解出的子问题与原始问题相似,而规模更小。这刚好符合递归的特性。因此,分治法往往与递归联系在一起。
说到这里,是不是有小伙伴觉得分治法与减治法很相似,傻傻分不清?我们这里再举f(n)=a^n的栗子。
n>1时:f(n)=a^(n/2)*a^(n/2)
n=1时:f(n)=a
比较一下减常数因子:
n是偶数时:f(n)= f(n/2)^2
n是大于1的奇数时:f(n)= f((n-1)/2)^2* a
n = 1时:f(n)=a
也就是说,分治法对分治出的部分需要分别处理,进行分开的单独计算,而减治法则利用了”一个问题给定实例的解和同样问题较小实例的解之间的关系”,只针对部分子问题求解,减治掉的那部分就不需要了。
其实,减常因子的减治法也可以看做是分治的变种。
需要注意的是,不是所有的分治算法都一定比简单蛮干更有效,前面的减治法也是,就比方说这里的栗子,时间复杂度仍为o(n)。不过,“通常我们向算法女神所做的祈祷都被应允了”,使用分治法往往比使用其他方法效率更高。
分治法的时间效率T(n)一般满足方程T(n)=aT(n/b)+f(n)。因此,分治法对于并行算法是非常理想的。
我们介绍一个和数学有关的算法:
Strassen矩阵乘法。
(虽然在骁老板的文章里有提到,但我还是不辞辛苦地再写一遍八)
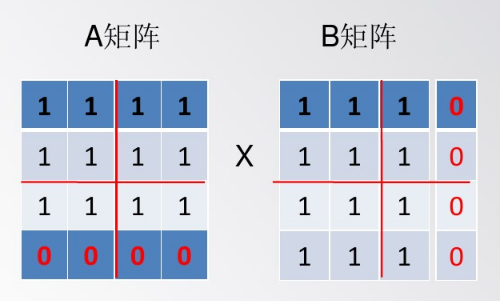
考虑到大家都是小白,先说明矩阵乘法的定义。(其实是我自己不懂才先去查的)
这张图很清楚的说明了矩阵乘法的计算公式。为了方便讲解,我们先以n*n的偶数阶方阵为例,之后再拓展到一般的矩阵乘法。
我们从数学中回到算法来。这个问题如果直接暴力计算,需要循环三次:关于i,j,k分别循环。时间复杂度为o(n^3)。
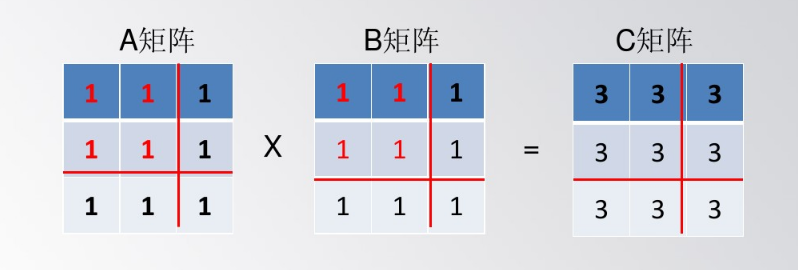
我们采用分治的思想,把偶数阶方阵如图划分为四份(这里的ABC可以是矩阵):
按照矩阵中的知识,可以得到:
C11 = A11 • B11 + A12 • B21
C12 = A11 • B12 + A12 • B22
C21 = A21 • B11 + A22 • B21
C22 = A21 • B12 + A22 • B22
我们估算一下时间复杂度:T(n) = 8T(n/2) + o(n^2)(前面是不是见过这个式子?)递归的结果是时间复杂度并没有降低。算法女神去死八。
聪明的Strassen不甘心。他发明了一种新的方法,通过降低递归式中T(n/2)的系数来降低时间复杂度。
仍然把每个矩阵分割为4份,然后创建如下10个中间矩阵:
S1 = B12 – B22
S2 = A11 + A12
S3 = A21 + A22
S4 = B21 – B11
S5 = A11 + A22
S6 = B11 + B22
S7 = A12 – A22
S8 = B21 + B22
S9 = A11 – A21
S10 = B11 + B12
接着,计算7次矩阵乘法,在建立7个中间的中间矩阵(中中间矩阵):
M1 = A11 • S1
M2 = S2 • B22
M3 = S3 • B11
M4 = A22 • S4
M5 = S5 • S6
M6 = S7 • S8
M7 = S9 • S10
最后,根据这7个中中间矩阵就可以计算出C矩阵:
C11 = M5 + M4 – M2 + M6
C12 = M1 + M2
C21 = M3 + M4
C22 = M5 + M1 – M3 – M7
证明就留给线性代数的同学们吧,应该不难。当然能不能想到就另说咯。
但不管怎么说,我们利用这个结论,成功地将系数8变成了7,算法的时间复杂度也就降低到了o(n^log7)。
我们再回到一般性矩阵。对于一般性矩阵,我们还是认真看定义吧。。。
对于非偶数阶方阵,我们可以用0将其填充为偶数阶方阵:
如果是奇数阶方阵,我们也可以在找到最近的偶数阶方阵,其余部分直接暴力计算。
(代码中我只实现第一种方式)
很明显这种优化是为了处理大型问题的,既然如此我们在写代码时也需要开辟足够大的规模。一种方法是用指针创建它(这就是代码冗长的主要原因)。因为是二维数组,所以需要用到指向指针的指针,再用数组表示指针,然后就可以用熟悉的处理数组的方式处理数据啦。
代码小长,实际上也没什么内容:
//strassen算法(在此感谢互联网,减少工作量) #include #include #include using namespace std;void Strassen(int N, int** MatrixA, int ** MatrixB, int ** MatrixC); //进行矩阵乘法 void ADD(int** MatrixA, int** MatrixB, int** MatrixResult, int length ); //矩阵加法 void SUB(int** MatrixA, int** MatrixB, int** MatrixResult, int length ); //矩阵减法 void MUL(int** MatrixA, int** MatrixB, int** MatrixResult ); //计算规模最小的二阶矩阵(常规方法) void FillMatrix( int** matrix, int, int,int); //输入原始矩阵 void PrintMatrix( int **Matrix, int length,int width ); //输出矩阵乘法结果 int findN(int l1,int l2,int l3,int l4); //非偶数阶方阵,寻找扩充边界 int main(){
int length1,length2,width1,width2; int** MatrixA; //指向指针的指针,存放矩阵数据 int** MatrixB; int** MatrixC; cout< cin>>length1>>width1; cin>>length2>>width2; int N =findN(length1,length2,width1,width2); MatrixA = new int *[N]; //开辟一维指针数组,每个数组容量为N MatrixB = new int *[N]; MatrixC = new int *[N]; for (int i = 0; i < N; i++) {
MatrixA[i] = new int [N]; //开辟二维数组 ,每个数组容量为N*N MatrixB[i] = new int [N]; MatrixC[i] = new int [N]; } cout< FillMatrix(MatrixA,length1,width1,N); FillMatrix(MatrixB,length2,width2,N); Strassen( N, MatrixA, MatrixB, MatrixC ); cout< int length3=length1>length2?length1:length2; PrintMatrix(MatrixC,length1,width2); return 0;}//寻找拓展规模N int findN(int l1,int l2,int l3,int l4){
int max,k=1,max1,max2; max1=l1>l2?l1:l2; max2=l3>l4?l3:l4; max=max1>max2?max1:max2; while (true) {
if (max<=pow(2,k)) return pow(2,k); k++; } } //计算矩阵乘法 void Strassen(int N, int **MatrixA, int **MatrixB, int **MatrixC){
int HalfSize = N/2; int newSize = N/2; if ( N == 2 ) //边界最小规模:二阶矩阵 {
MUL(MatrixA,MatrixB,MatrixC); } else {
//和主函数里一样,定义指针,开辟空间 int** A11; int** A12; int** A21; int** A22; int** B11; int** B12; int** B21; int** B22; int** C11; int** C12; int** C21; int** C22; int** M1; int** M2; int** M3; int** M4; int** M5; int** M6; int** M7; int** AResult; //result返回结果 int** BResult; A11 = new int *[newSize]; A12 = new int *[newSize]; A21 = new int *[newSize]; A22 = new int *[newSize]; B11 = new int *[newSize]; B12 = new int *[newSize]; B21 = new int *[newSize]; B22 = new int *[newSize]; C11 = new int *[newSize]; C12 = new int *[newSize]; C21 = new int *[newSize]; C22 = new int *[newSize]; M1 = new int *[newSize]; M2 = new int *[newSize]; M3 = new int *[newSize]; M4 = new int *[newSize]; M5 = new int *[newSize]; M6 = new int *[newSize]; M7 = new int *[newSize]; AResult = new int *[newSize]; BResult = new int *[newSize]; int newLength = newSize; //同上 for ( int i = 0; i < newSize; i++) {
A11[i] = new int[newLength]; A12[i] = new int[newLength]; A21[i] = new int[newLength]; A22[i] = new int[newLength]; B11[i] = new int[newLength]; B12[i] = new int[newLength]; B21[i] = new int[newLength]; B22[i] = new int[newLength]; C11[i] = new int[newLength]; C12[i] = new int[newLength]; C21[i] = new int[newLength]; C22[i] = new int[newLength]; M1[i] = new int[newLength]; M2[i] = new int[newLength]; M3[i] = new int[newLength]; M4[i] = new int[newLength]; M5[i] = new int[newLength]; M6[i] = new int[newLength]; M7[i] = new int[newLength]; AResult[i] = new int[newLength]; BResult[i] = new int[newLength]; } //拆分A、B矩阵为四个小矩阵 for (int i = 0; i < N / 2; i++) {
for (int j = 0; j < N / 2; j++) {
A11[i][j] = MatrixA[i][j]; A12[i][j] = MatrixA[i][j + N / 2]; A21[i][j] = MatrixA[i + N / 2][j]; A22[i][j] = MatrixA[i + N / 2][j + N / 2]; B11[i][j] = MatrixB[i][j]; B12[i][j] = MatrixB[i][j + N / 2]; B21[i][j] = MatrixB[i + N / 2][j]; B22[i][j] = MatrixB[i + N / 2][j + N / 2]; } } //计算7个中中间矩阵 M //M1=(A11+A22)*(B11+B22) ADD( A11,A22,AResult, HalfSize); ADD( B11,B22,BResult, HalfSize); Strassen( HalfSize, AResult, BResult, M1 ); //M2=(A21+A22)*B11 ADD( A21,A22,AResult, HalfSize); Strassen(HalfSize, AResult, B11, M2); //M3=A11*(B12-B22) SUB( B12,B22,BResult, HalfSize); Strassen(HalfSize, A11, BResult, M3); //M4=A22(B21-B11) SUB( B21, B11, BResult, HalfSize); Strassen(HalfSize, A22, BResult, M4); //M5=(A11+A12)B22 ADD( A11, A12, AResult, HalfSize); Strassen(HalfSize, AResult, B22, M5); //M6=(A21-A11)(B11+B12) SUB( A21, A11, AResult, HalfSize); ADD( B11, B12, BResult, HalfSize); Strassen( HalfSize, AResult, BResult, M6); //M7=(A12-A22)(B21+B22) SUB(A12, A22, AResult, HalfSize); ADD(B21, B22, BResult, HalfSize); Strassen(HalfSize, AResult, BResult, M7); //计算出新矩阵的四个部分C //C11 = M1 + M4 - M5 + M7; ADD( M1, M4, AResult, HalfSize); SUB( M7, M5, BResult, HalfSize); ADD( AResult, BResult, C11, HalfSize); //C12 = M3 + M5; ADD( M3, M5, C12, HalfSize); //C21 = M2 + M4; ADD( M2, M4, C21, HalfSize); //C22 = M1 + M3 - M2 + M6; ADD( M1, M3, AResult, HalfSize); SUB( M6, M2, BResult, HalfSize); ADD( AResult, BResult, C22, HalfSize); //合并为新矩阵 for (int i = 0; i < N/2 ; i++) {
for (int j = 0 ; j < N/2 ; j++) {
MatrixC[i][j] = C11[i][j]; MatrixC[i][j + N / 2] = C12[i][j]; MatrixC[i + N / 2][j] = C21[i][j]; MatrixC[i + N / 2][j + N / 2] = C22[i][j]; } } // 释放空间 for (int i = 0; i < newLength; i++) {
delete[] A11[i];delete[] A12[i];delete[] A21[i];delete[] A22[i]; delete[] B11[i];delete[] B12[i];delete[] B21[i];delete[] B22[i]; delete[] C11[i];delete[] C12[i];delete[] C21[i];delete[] C22[i]; delete[] M1[i];delete[] M2[i];delete[] M3[i];delete[] M4[i];delete[] M5[i];delete[] M6[i];delete[] M7[i]; delete[] AResult[i];delete[] BResult[i] ; } delete[] A11;delete[] A12;delete[] A21;delete[] A22; delete[] B11;delete[] B12;delete[] B21;delete[] B22; delete[] C11;delete[] C12;delete[] C21;delete[] C22; delete[] M1;delete[] M2;delete[] M3;delete[] M4;delete[] M5; delete[] M6;delete[] M7; delete[] AResult; delete[] BResult ; }} //计算矩阵加法 ,记过输入result void ADD(int** MatrixA, int** MatrixB, int** MatrixResult, int MatrixSize ){
for ( int i = 0; i < MatrixSize; i++) {
for ( int j = 0; j < MatrixSize; j++) {
MatrixResult[i][j] = MatrixA[i][j] + MatrixB[i][j]; } }} //矩阵减法,同上 void SUB(int** MatrixA, int** MatrixB, int** MatrixResult, int MatrixSize ){
for ( int i = 0; i < MatrixSize; i++) {
for ( int j = 0; j < MatrixSize; j++) {
MatrixResult[i][j] = MatrixA[i][j] - MatrixB[i][j]; } }} //暴力法求解,计算二阶矩阵 void MUL( int** MatrixA, int** MatrixB, int** MatrixResult ){
for (int i=0;i<2 ;i++) {
for (int j=0;j<2 ;j++) {
MatrixResult[i][j]=0; for (int k=0;k<2 ;k++) {
MatrixResult[i][j]=MatrixResult[i][j]+MatrixA[i][k]*MatrixB[k][j]; } } }}//输入数据 ,填充为偶数阶方阵 void FillMatrix( int** Matrix, int length,int width,int N){
for(int row = 0; row {
if (row {
for(int column = 0; column {
if (column cin>>Matrix[row][column]; else Matrix[row][column]=0; } } else {
for(int column = 0; column Matrix[row][column]=0; } }}//输出正确规模的新矩阵 void PrintMatrix(int **MatrixA,int length,int width){
cout< for(int row = 0; row {
for(int column = 0; column {
cout< if ((column+1)%((width)) == 0) cout< } } cout<}(检验用了小一点的数组,别介意。。。)
03
变 治 法
I don’ t konw it’ s English name
生活的秘密在于。。。用一个烦恼代替另一个烦恼。
——Charles M. Schulz (1922 – 2000),美国漫画家
变治法,就是基于变换的一种思想方法,首先把问题的实例变得容易求解,然后进行求解。这个方法的思路类似于数学建模的思路,将生活中的问题进行简单的抽象、归化,以便对此进行研究。它不是一种标准的算法,更多的是一种思考的方式。
变治法的工作可以分成两个阶段:首先把问题变得更容易求解,然后对实例进行求解。根据我们对问题实例的变换方式,变治思想有3种主要的类型:
1.实例化简(Instance simplification)。
2.改变表现(Representation Change).
3.问题化简(Problem reduction).
1.实例化简(Instance simplification)。
指将原问题变换为同样问题的一个更简单或者更方便的实例。
预排序是一个这样的栗子:
预排序并不是一种算法设计策略,而是一种意识,在设计算法时要有这种意识,在算法中作预处理,是一种将实例化简的变治策略。
我们在构建数据时就提前进行排序,处理一些问题时就可以非常方便。
例如检验数组元素的唯一性。如果没有预排序,只用蛮力法,需要经过两轮循环,一个个元素检查,时间复杂度为o(n^2)。
而将数组预排序后,相同的元素就会挨着,扫描一遍比较两侧的数据后即可检验元素唯一性,扫描过程的时间复杂度为o(n)。(当然,排序的时间复杂度会更大)
再如模式计算。模式是指一个序列中出现次数最多的一个数值。
同样,如果用蛮力,逐个检查元素出现的次数,需要两遍扫描,复杂度为o(n^2)
预排序将相同的元素紧挨着,通过一遍扫描,累计元素重复出现过的次数,就可知道出现最多的元素。同上,时间复杂度为o(n)。
同理的还有查找问题,这里就不再说了。代码就是排序,也不写了。
2.改变表现(Representation Change).
指将原问题变换为同样实例的不同表现。
我们介绍一个很经典的栗子:霍纳法则。
在计算多项式时,人为计算一般都是一项一项算;然而,当计算机这样计算时,每次求k次方都需要进行多次乘法,效率相当低。
因此,我们将乘法改变为以下形式:
这样,我们只需要进行n次乘法,通过改变了式子(即问题)的表现形式,大大优化了效率。
代码也非常简单,就不写了。(咱们注重思想哈,不是偷懒)
3.问题化简(Problem reduction).
指将原问题变换为另一个问题的实例,这种问题的算法是已知的。(归化思想)转换的难题在于如何找到一个变换的目标算法。
线性规划就是一个很好的目标。我们这里以背包问题为例。
在之前的文章中,我们曾用回溯法解决01背包问题。实际上,背包问题的本质是线性规划。了解了线性规划的本质后,才能更好地解决高维的背包问题。
在高中大家都学过线性规划。线性规划是一种非常好理解的方法,但我们高中的运用大多局限于二维空间。我们将它拓展到n维空间。
在二维空间里,一条的直线Ax+By+C=0能将二维平面分割为两部分。
同样,在三维空间里,Ax+By+Cz+D=0表示一个二维平面,可以将三维空间分割为两个部分。
那么,拓展到n维呢?
一个(n-1)维的分割线,可以将一个n维物体分作两份。
看这样一条分割线:
A0t0+A1t1+A2t2+…+Antn+An+1=0
我们把n个变量看做n个自变量tn,也就是在n维空间里思考。利用一系列约束条件的方程求出可行域,在寻找最优解——一切就变得想高中时一样好理解,自然而然地上升到了n维。哪怕你不清楚n维空间长什么样,在2、3维空间下思考,起码能让问题变得更形象一些。
那么,对于背包问题,我们可以转化为以下不等式组:
其中ni表示第i个物品取几个,vi表示价值,wi表示重量。
0<=w1n1+w2n2+w3n3+…+wnnn<=W
V= v1n1+v2n2+v3n3+…+vnnn
求V的最大值。
(对01背包问题而言,nk只能取0或1.)
背包问题就这样一步步转化为线性规划的问题啦。然而,这个问题也不那么好解决。这里我们就不解决了,等到未来的某天再填上这个坑吧。(相信我们未来还会再遇到背包问题的)
那么,这期的文章就到这儿结束了。
因为一直觉得总结部分很水,所以这次去掉了。。。
感觉这期的代码都和算法本身关系不大?
的确,这次的算法都不是那么的标准。
但依然提供给我们更多看问题的角度,要学会动态地看问题。
那么,赶完这期的我又要继续忙别的去了。。。
考试在即,无力脱身,让我们下次再见~!
#
-The End-
文/即将要考cpp十分紧张的舟新手
版/同时还要考微积分的没时间学数学的小白舟
码/猛然发现英语已经好久都没学的工人舟
审/貌似好久都没更新的很忙的老板短短的路走走停停
#
今天的文章最大公约数简便算法_【算法学习】减治 分治 变治分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/63109.html