堆排序过程图解_小顶堆排序怎么排

0. 前言

Biu

堆排序是一个不稳定的排序算法，对数据不敏感，时间复杂度稳定，主要分为两部分：建堆、堆排序。

其中建堆的时间复杂度是 $O(n)$ 的，而排序选出一个最大、最小值的过程是 $O(logn)$ 的，一共需要 n 次操作，故总共的时间复杂度是 $O(nlogn)$ 的。

堆主要的两个操作，在此仅使用向下调整 down() 操作即可，至于另一个注意点就是堆排序的建堆时间复杂度计算了，和树的高度密切相关，通过数学式子可以严格证明它是 $O(n)$ 的时间复杂度。

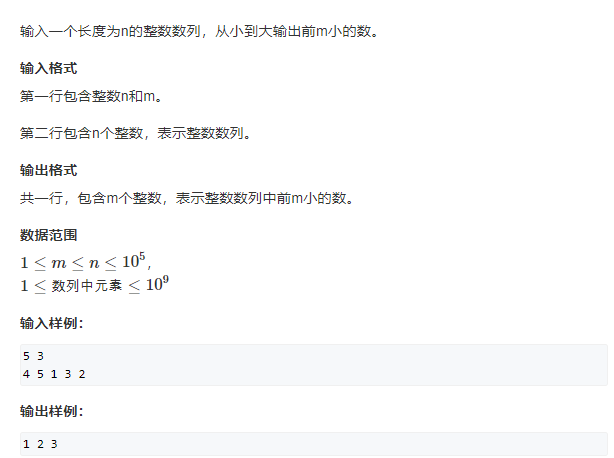
1. 堆排序

代码：

#include <iostream>

using namespace std;

const int N = 1e5+5;

int n, m;
int h[N], tt;

void down(int u) { 
   
    int t = u;  // t表示三个数中最小值编号
    if (u * 2 <= tt && h[u * 2] < h[t]) t = u * 2;    // 如果有左儿子并且左儿子比它小更新为左儿子
    if (u * 2 + 1 <= tt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) swap(h[u], h[t]), down(t);      // 当前根节点不是最小的，交换一下，递归处理即可
}

void up(int u) { 
   
    while (u / 2 && h[u / 2] > h[u]) swap(h[u], h[u / 2]), u /= 2;
}

int main() { 
   
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> h[i];
    tt = n;
    
    // 递归的O(n)建堆，时间不是O(logn)注意
    // 从倒数第二层开始down，保证当前节点的左右儿子已经是堆了
    for (int i = n / 2; i; --i) down(i); 
    
    while (m --) { 
   
        cout << h[1] << ' ';
        h[1] = h[tt];
        tt--;
        down(1);
    }
    
    return 0;
}

今天的文章堆排序过程图解_小顶堆排序怎么排分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。