海洋捕食者算法介绍及TSP求解代码实现

前言

在准备建模比赛的时候看到了海洋捕食者算法，说是可以用来求解优化问题。虽然目前网上文献比较少，但据我查的一些资料说MPA效率比粒子群和GA都要好，所以想要学习实践一下

一、海洋捕食者算法是什么？

海洋捕食者算法 ( Marine Predators Algorithm，MPA) 是Afshin Faramarzi 等人于 2020 年提出的一种新型元启发式优化算法，其灵感来源于海洋适者生存理论，即海洋捕食者通过在Lévy 游走或布朗游走之间选择最佳觅食策略。具有寻优能力强等特点。模拟了海洋中捕食者和猎物的进化演绎。在算法中独有的海洋记忆存储阶段与海洋漩涡影响阶段比较难理解。

二、MPA的具体内容

1.思想

算法认为顶级捕食者有最大的搜索本领，可以搜索到最舒适的环境（最优解）。
tips:这里是我的个人理解

2.相关术语

• 猎物：种群中的全部个体

• 精英：种群中的捕食者，注意猎物和捕食者的身份可能互换，所以精英是不断更新的。

• 猎物矩阵Prey：规模为n*m，n代表种群中个体数目，m代表个体的属性维度（问题解的维度）

• 精英矩阵Elite：和Prey规模相同

• 布朗随机游走：概念接近于布朗运动，是布朗运动的理想数学状态。任何无规则行走者所带的守恒量都各自对应着一个扩散运输定律。（大概意思就是一种随机的分布）

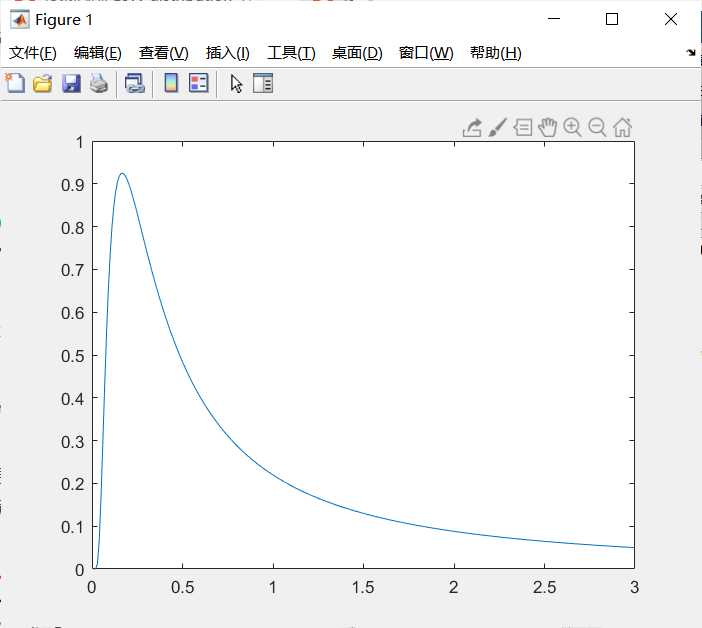
• Levy分布：列维分布是非负随机变量的连续概率分布，绘图如下
  

• 涡流及鱼类聚集效应(FADs)：鱼群喜欢聚集在某个地方，可以引申为局部最优解

3.过程

步骤1：设定算法参数，初始化种群。

步骤2：计算猎物矩阵(Prey)适应度值，记录最优位置，计算出精英矩阵(Elite)

步骤3：捕食者根据迭代阶段，选择对应的更新方式，更新捕食者位置

• 阶段一：迭代初期（当前代次小于最大迭代次数1/3），进行全局搜索，通过布朗随机游走更新Prey
• 阶段二：迭代中期（当前代次小于最大迭代次数2/3），种群被分为两部分，其中猎物做Levy运动，负责算法在搜索空间内开发，捕食者做布朗运动，负责算法在搜索空间内探索：
• 阶段三：迭代后期（当前代次大于最大迭代次数2/3)，主要提高算法的局部开发，此时捕食者的策略为Levy运动：

步骤4：计算适应度值，更新最优位置。

步骤5：解决涡流形成和FADs效应：让算法在迭代过程中尽可能跳出局部最优解。

步骤6：判断是否满足停止条件，如果不满足则重复步骤2-5，否则输出算法最优结果。

三、用MPA求解旅行商(TSP)问题

1.TSP简介

旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个人要去若干个城市，他从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。
从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。
由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

2.过程与问题

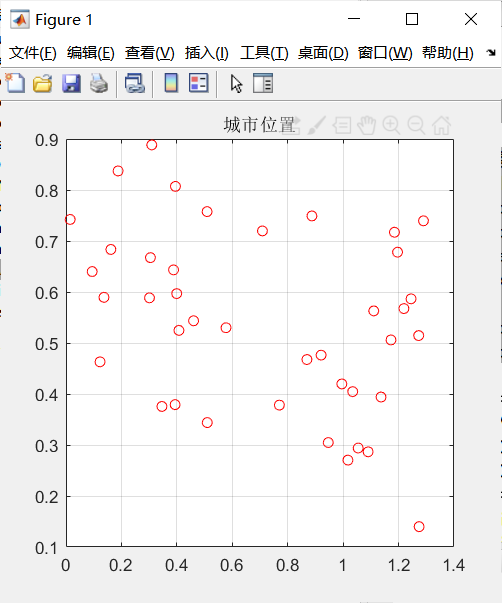
1.首先导入了40个城市的二维平面坐标，我将其绘图如下

2.进行参数初始化

• 种群中个体数目=50
  最大迭代次数=5000

• 写好适应度函数：也就是路径长度（优化目标是长度越短越好）

• 初始化一些矩阵

• Iter=0; （记录迭代次数）
  FADs=0.2;
  P=0.5;

3.开始循环(5000次迭代）
while(Iter<Max_Iter)

探测顶级捕食者
海洋记忆，更新精英矩阵
计算适应度
根据不同阶段更新猎物矩阵
探测顶级捕食者
海洋记忆，更新精英矩阵
解决涡旋问题，跳出局部最优

Iter=Iter+1

end
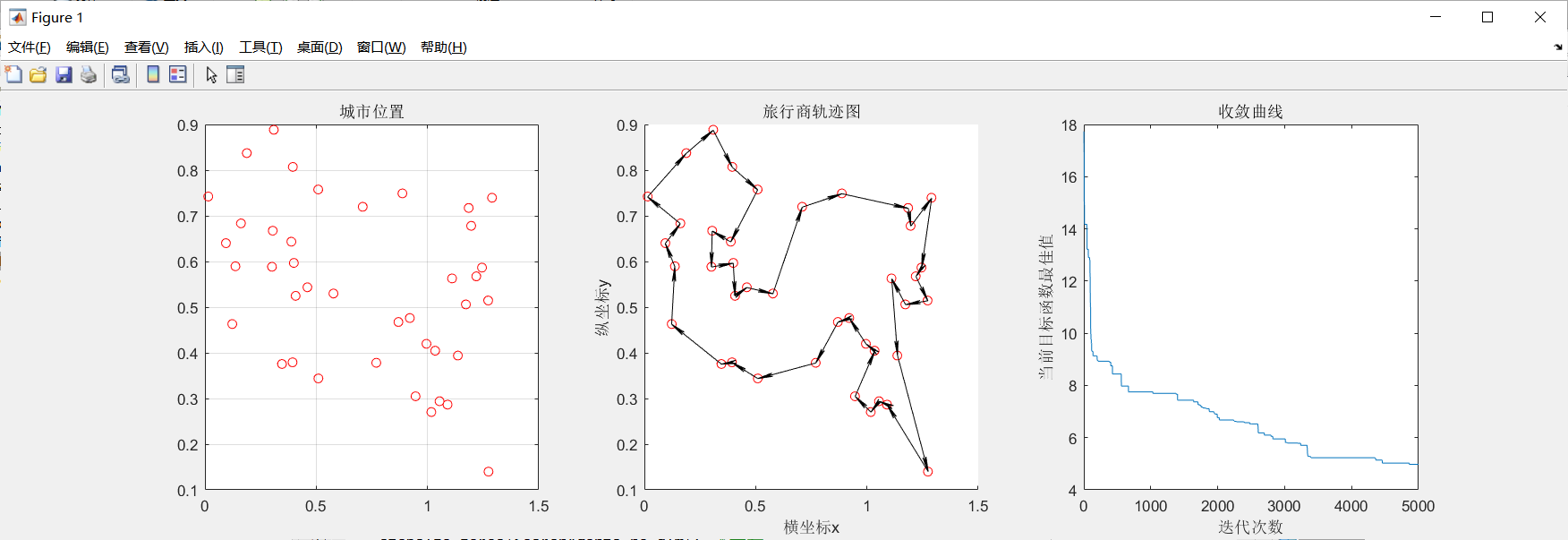
4.对结果和迭代过程绘图


5.在写代码过程中遇到的问题
最大的一个问题是如何表示路径
在猎物矩阵Prey中，有25个个体，每个个体有40个维度，也就是分别代表40个城市的顺序。
在模拟退火中，可以初始化40个不重复整数，然后对其扰动：二交换或三交换。而在海洋捕食者算法中，种群的更新是基于两个随机分布确定的，会出现小数，这就代表不了城市编号。我前后想了几种方法，最终得以解决：
一开始，我选择将小数四舍五入为整数，后来发现这样是不行的，可能会有多个小数四舍五入为一个整数，这样造成算法优化出的最优路径为停留一个城市（因为这样的最短路长为0）。
最终我的解决方案是将小数排序，间接表示城市，40个小数按顺序编号，它们的编号即是40个城市的序号，这样既利于了随机分布特性，又满足了整数约束。

3.代码

代码是用matlab编写的

主程序是main_MPA.m
还有若干封装函数：

• Distance：求城市之间两两距离
• InitPop：初始化种群
• Get_Functions_details：获取适应度函数的信息
• levy：计算列维分布的函数
• DrawPath：根据路径画图
• dsxy2figxy：坐标转换函数

主程序代码：

%求解旅行商主程序%
tic
clear;
clc;
close all;
load locations;

D = Distance(locations);    %计算城市两两之间的距离(矩阵）
%画出城市分布图
x = locations(:,1);  y = locations(:,2);
subplot(1,3,1);  
plot(x,y,'ro');
title('城市位置');  grid on;
set(gcf,'position',[50,200,1400,400]);  %设定图形的位置和大小

format long;

%------------------ 开始运行MPA ------------------%
%初始化参数
SearchAgents_no=50; %种群中个体数目
Max_iteration=5000; % 最大迭代次数
[lb,ub,dim,fobj]=Get_Functions_details();%获取函数相关信息，fobj是适应度函数句柄
Top_predator_pos=zeros(1,dim);
Top_predator_fit=inf;

Convergence_curve=zeros(1,Max_iteration);  %初始化收敛曲线（记录每次的最优解）
stepsize=zeros(SearchAgents_no,dim);  %步长
fitness=inf(SearchAgents_no,1);  %种群中个体的适应度

Prey=InitPop(SearchAgents_no,dim,ub,lb);  %初始化种群
Path=zeros(SearchAgents_no,dim);   %初始化路径

Xmin=repmat(ones(1,dim).*lb,SearchAgents_no,1);
Xmax=repmat(ones(1,dim).*ub,SearchAgents_no,1);

%固定参数
Iter=0;
FADs=0.2;
P=0.5;

while Iter<Max_iteration
    %------------------- 探测顶级捕食者-----------------
    
    for i=1:size(Prey,1)  %对每个个体
        
        Flag4ub=Prey(i,:)>ub;
        Flag4lb=Prey(i,:)<lb;
        Prey(i,:)=(Prey(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        
        %精髓之处：因为这里的随机运动会让个体变成小数，所以选择用排序的序号表示城市。
        [~,Path(i,:)]=sort(Prey(i,:));   
        fitness(i,1)=fobj(D,Path(i,:));
       
        if fitness(i,1)<Top_predator_fit   %记录适应度最优的个体为捕食者(这里为极小型）
            Top_predator_fit=fitness(i,1);
            Top_predator_pos=Prey(i,:);
        end
    end
    
    %------------------- 海洋记忆，更新精英矩阵 -------------------
    
    if Iter==0
        fit_old=fitness;    
        Prey_old=Prey;
    end
    
    Inx=(fit_old<fitness);
    Indx=repmat(Inx,1,dim);  %repmat复制函数，indx是一个只含0，1的矩阵
    %更新Prey和fitness
    Prey=Indx.*Prey_old+~Indx.*Prey;  
    fitness=Inx.*fit_old+~Inx.*fitness;
    
    fit_old=fitness;    Prey_old=Prey;
    
    %------------------------------------------------------------
    
    Elite=repmat(Top_predator_pos,SearchAgents_no,1);  %(Eq. 10)
    CF=(1-Iter/Max_iteration)^(2*Iter/Max_iteration);
    
    RL=0.05*levy(SearchAgents_no,dim,1.5);   %Levy随机数向量
    RB=randn(SearchAgents_no,dim);           %Brownian随机数向量
    
    for i=1:size(Prey,1)
        for j=1:size(Prey,2)
            R=rand();
            %------------------阶段 1  -------------------
            if Iter<Max_iteration/3
                stepsize(i,j)=RB(i,j)*(Elite(i,j)-RB(i,j)*Prey(i,j));
                Prey(i,j)=Prey(i,j)+P*R*stepsize(i,j);
                
                %--------------- 阶段 2 ----------------
            elseif Iter>Max_iteration/3 && Iter<2*Max_iteration/3
                
                if i>size(Prey,1)/2
                    stepsize(i,j)=RB(i,j)*(RB(i,j)*Elite(i,j)-Prey(i,j));
                    Prey(i,j)=Elite(i,j)+P*CF*stepsize(i,j);
                else
                    stepsize(i,j)=RL(i,j)*(Elite(i,j)-RL(i,j)*Prey(i,j));
                    Prey(i,j)=Prey(i,j)+P*R*stepsize(i,j);
                end
                
                %----------------- 阶段 3 -------------------
            else
                
                stepsize(i,j)=RL(i,j)*(RL(i,j)*Elite(i,j)-Prey(i,j));
                Prey(i,j)=Elite(i,j)+P*CF*stepsize(i,j);
                
            end
        end
    end
    
    %------------------ 探测顶级捕食者 ------------------
    for i=1:size(Prey,1)
        
        Flag4ub=Prey(i,:)>ub;
        Flag4lb=Prey(i,:)<lb;
        Prey(i,:)=(Prey(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        
            
        [~,Path(i,:)]=sort(Prey(i,:));
        fitness(i,1)=fobj(D,Path(i,:));
        
        if fitness(i,1)<Top_predator_fit
            Top_predator_fit=fitness(i,1);
            Top_predator_pos=Prey(i,:);
        end
    end
    
    %---------------------- 海洋记忆 ----------------
    
    if Iter==0
        fit_old=fitness;    Prey_old=Prey;
    end
    
    Inx=(fit_old<fitness);
    Indx=repmat(Inx,1,dim);
    Prey=Indx.*Prey_old+~Indx.*Prey;
    fitness=Inx.*fit_old+~Inx.*fitness;
    
    fit_old=fitness;    Prey_old=Prey;
    
    %---------- 解决涡流形成和FADS效应 -----------
    
    if rand()<FADs
        U=rand(SearchAgents_no,dim)<FADs;
        Prey=Prey+CF*((Xmin+rand(SearchAgents_no,dim).*(Xmax-Xmin)).*U);
        
    else
        r=rand();  Rs=size(Prey,1);
        stepsize=(FADs*(1-r)+r)*(Prey(randperm(Rs),:)-Prey(randperm(Rs),:));
        Prey=Prey+stepsize;
    end
    
    Iter=Iter+1;
    Convergence_curve(Iter)=Top_predator_fit;
end

[~,Best_Path]=sort(Top_predator_pos);
Best_score=Top_predator_fit;

%绘制收敛曲线
subplot(1,3,2);
Draw_Path(Best_Path,locations);
subplot(1,3,3);
plot(Convergence_curve);
title('收敛曲线')
xlabel('迭代次数');
ylabel('当前目标函数最佳值');

display(['MAP得到的最优解为: ' num2str(Best_Path,5) '>>']);
display(['MPA找到的目标函数的最佳值为 : ', num2str(Best_score,10)]);
fprintf('--------------------------------------------------------\n');
toc

4.对比

运行时间大约30s
比起遗传算法和模拟退火，此算法时间效率更高，大概提高了两倍，但是不稳定，这也是优化算法的通病吧。

附件

完整matlab代码链接

今天的文章海洋捕食者算法介绍及TSP求解代码实现分享到此就结束了，感谢您的阅读。