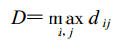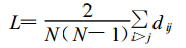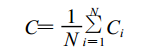复杂网络综述

本人毕业设计是关于复杂网络的，之前完全没听说过的概念，于是就在网上找了一些论文来看，顺便做下笔记，这篇文章主要讲了复杂网络的一些基础概述。
这里的网络不是（不仅仅是）计算机网络这门课中的网络，它表示的是任何一个可以用节点和节点之间连线来代表的一个系统，如：神经系统可以看做是大量神经细胞通过神经纤维相互连接形成的网络。

• 拓扑结构
  拓扑结构就是们把网络不依赖于节点的具体位置 和边的具体形态就能表现出来的性质叫做网络的拓扑性质 ,相应的结构叫做网络的拓扑结构。
  通俗点说就是任何网络结构不管他的节点是什么，边是怎样的，把节点当做点，把点当做线，只关心它是怎样连接的，这就是网络的拓扑结构。

• 复杂网络的由来
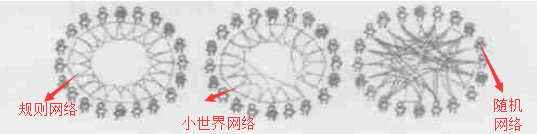
  科学家们企图用一种通用的拓扑结构来将真实世界中的各种系统表示出来，期间经历了三个阶段：

  • 1 用一种固定的规则的结构表示：如二维平面上的欧几里得网格
  • 2 节点之间的边不再是确定的，而是用一个概率决定，也就是随机网络
  • 3 真实网络既不是规则的也不是随机的，而是一种与前两种不同的统计特征网络，即复杂网络。

• 复杂网络概念
  百度百科给出的复杂网络的定义是：复杂网络（Complex Network），具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络。

  下面先给出小世界效应和无标度网络的概念：

• 小世界效应
  在给出小世界概念效应之前，先说一下什么是簇系数和网络的平均距离：

  • 平均距离
    两点间的距离被定义为连接两点的最短路所包含的边的数目，把所有节点对的距离求平均就是网络的平均距离。
  • 簇系数
    对于某个节点，它的簇系数被定义为它所有相邻节点之间连边数目占可能的最大连边数目的比例。（比如一个节点和三个节点相连，则它相邻的这三个节点的最大连边数目为3，加入实际只有其中两个节点相连，则该节点簇系数为1/3）。网络的簇系数是所有节点簇系数的平均值。

  
  规则网络具有大的簇系数和大的平均距离（任何一个节点的度都相同）
  随机网络具有小的簇系数和小的平均距离（ER随机图的许多重要特性都是突然涌现的，也就是说给定边相连的概率P，要么几乎所有图都有某个性质，要么几乎所有图都不具有该性质）
  小世界网络具有大的簇系数和小的平均距离
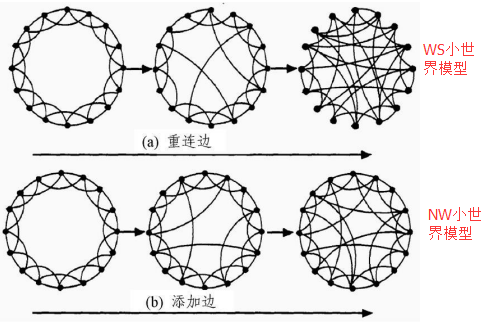
  （小世界网络是在规则网络不改变原有边的基础上，以一个小的概率在原有网络上添加新边）
  小世界效应：大的簇系数和小的平均距离两个统计特征合在一起称为小世界效应。具有这种效应的网络就是小世界网络。
  （真实网络几乎都具有小世界效应）
  
  （该图就是小世界网络的构造方法）

• 无标度网络
  节点度服从幂律分布就是说, 具有某个特定（出/入）度的节点数目与这个特定的度之间的关系可以用一个幂函数近似地表示。幂函数曲线是一条下降相对缓慢的曲线 ,这使得度很大的节点可以在网络中存在。对于随机网络和规则网络 ,度分布区间非常狭窄 ,几乎找不到偏离节点度均值较大的点 ,故其平均度可以被看作是其节点度的一个特征标度.
  在这个意义上 ,我们把节点度服从幂律分布的网络叫做无标度网络, 并称这种节点度的幂律分布为网络的无标度特性.
  无标度网络构造方法：
  

  网络的拓扑结构决定了网络所拥有的特性。 复杂网络表现出了与经典的随机图模型理论不同的特性。

  下面用实际生活中的例子说明小世界效应和无标度网络：
  小世界效应：小世界模型反映了朋友关系网络的一种特性, 即大部分人的朋友都是他们日常生活中经常接触的。 另外, 也有一些朋友离得很远, 甚至异国他乡。 正是由于这种不同朋友圈之间的长程连接, 导致了网络具有较小的平均路径长度。著名的“六度分离(Six degrees of separation) ”实验, 在某种程度上反映了人际关系的“小世界”特征。

  无标度网络：幂律分布的形成, 主要是由于节点的偏附依好(preferential attachment),即新加入网络的节点倾向于与那些具有较大度的节点相连, 这种现象也称为“马太效应(M atthew effect)”, 主要反映了人们的从众心理。

• 复杂网络的鲁棒性和脆弱性
  对网络节点的攻击主要有随机攻击和针对重要节点的攻击。
  复杂网络对于随机攻击具有较强的鲁棒性，即使众多节点被摧毁也不一定导致网络的瘫痪崩溃；然而众多重点节点被攻击的话，整个网络将会崩溃。

• 复杂网络的社区结构
  社区就是网络中节点的集合, 社区中的节点之间具有紧密的连接, 而社区之间则为松散的连接。 它体现了复杂系统的层次和模块结构。（如同大学校园里的抱团行为）

• 复杂网络的基本拓扑结构与图论
  复杂网络的基本拓扑结构可以用图论的方法表示成 G =(V , E), V 中元素称为节点或顶点(Vertex 或 Node), E 中元素称为边(Edeg或Link)。 在图论框架下, 可用不同的全局参量来表示复杂网络的特征, 最基本特征包括度分布 P(k)、平均路径长度L和聚类系数C。

  • 度分布
    节点的度指的是与该节点连接的边数。
    所有节点的度的平均值称为网络的平均度。
    网络中度分布函数的含义是：任意选择的节点恰度为K的概率；也就是网络中度为K的节点与总节点的个数比值。

  • 平均路径长度
    网络中两个节点 i 和 j 之间的距离d ij 定义为连接这两个节点的最短路径上的边数。 网络直径定义为网络中任意两个节点之间的距离的最大值, 记为 D :
    网络的平均路径长度 L 定义为两个节点之间的距离的
    平均值:
    式中, N 为网络节点数。 网络的平均路径长度也称为网络的
    特征路径长度。 一般来说, 真实网络有较短的平均路径长度。

  • 聚类系数
    节点 i 的聚类系数为与它相连接的k i 个节点彼此之间也相连的概率:
    
    式中, Ei是这ki个节点之间实际存在的边数。这ki个节点之间最多可能有k i(ki-1)/2条边。
    网络的平均聚类系数为:

  以上是一些关于复杂网络的部分基础概念，后面一篇博客将介绍复杂网络中重要节点挖掘的相关方法算法复杂网络中重要节点挖掘方法综述，如果有大神愿意指点我最好不过了^-^
  Q：386284750

  注：转载请注明原文出处：
  作者：CUG_UESTC
  出处：http://blog.csdn.net/qq_31192383/article/details/53043606

参考文献：
[1]周涛,柏文洁,汪秉宏,刘之景,严纲. 复杂网络研究概论. 物理. 2005年01期:31-35
[2]赫南,李德毅,淦文燕,朱熙. 复杂网络中重要性节点发掘综述. 计算机科学. 2007年12期:1-5
[3]陈端兵,黄晟,尚明生. 复杂网络模型及其在疫情传播和控制中的应用研究. 计算机科学. 2011年06期:118-121

今天的文章复杂网络综述分享到此就结束了，感谢您的阅读。