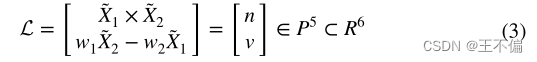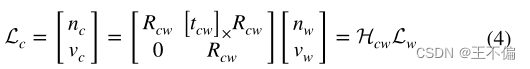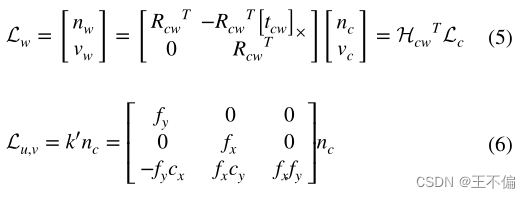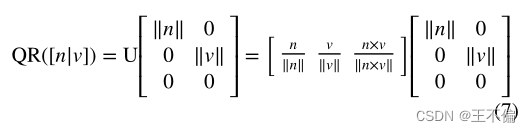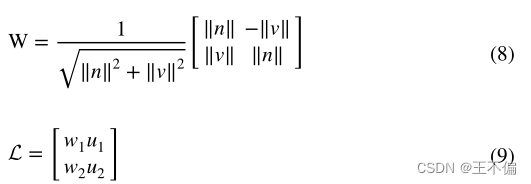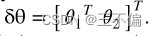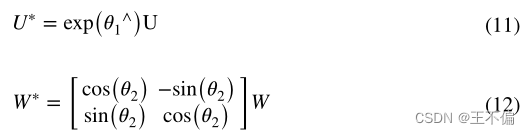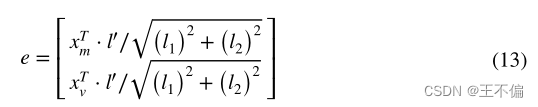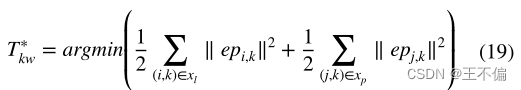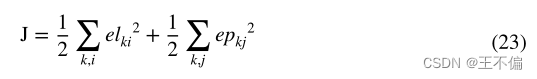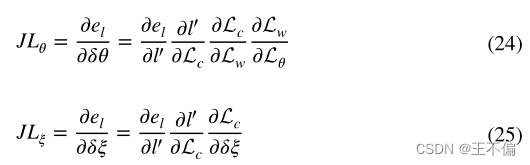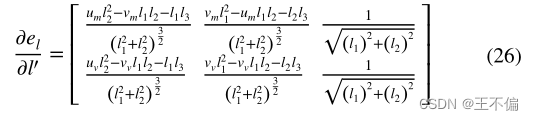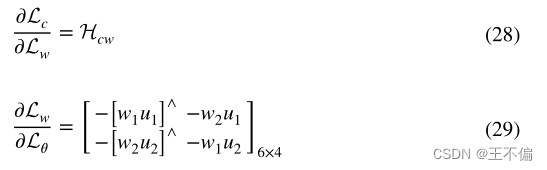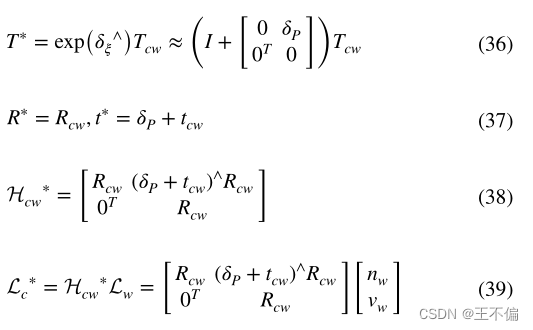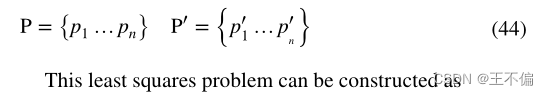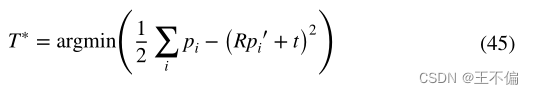PSL‑SLAM:PSL‑SLAM: a monocular SLAM system using points and structure lines in Manh 曼哈顿世界中的点线单目SLAM

文章下载地址：https://download.csdn.net/download/weixin_50508111/85811572

一.文章简介

1. 文章类型/时间/作者/所属单位： 期刊论文/2021.08/Feng Yang1 · Yichao Cao2 · Weigong Zhang/东南大学；
2. 主要工作：
（1）.利用结构线方向与消失点方向的一致性来提取结构线;
（2）.在优化模块中，将结构线的误差模型引入非线性优化框架，提出了一种新的优化策略；
（3）
3. 解决了什么问题：
（1）;
（2）；
（3）
4. 用了什么方法：
（1）线特征参数化方法：使用标准正交表示法（是不是就是2中的端点叉乘）来参数化直线。在本文中，使用更紧凑的Plucker坐标表示(Sola et al. 2009)和正交表示(Bartoli et al. 2005)来参数化空间直线;
Pluck坐标表示是一种6自由度的表示，在表示变换和重投影时具有良好的线性性质。
正交表示虽然在表示坐标变换时不如Pulk坐标的线性特性好，但在迭代求解直线在空间中的位置时，它具有良好的导数特性。
由于正交表示只有4个自由度，因此在优化过程中不会引入额外的约束，适用于后端优化。然而，在前端视觉里程表中很难表达重投影变换，因此本文仅在后端优化中使用正交表示，在其他情况下使用Plück坐标。
（2）计算消失点:目前的消失点提取算法可以表示为以下两类(Lu 2017):(1)基于ransac的方法。通过定义最小解集，随机选取满足最小解集个数的求交点的直线作为假设的灭点，计算剩余的直线是否满足该假设。(2)穷举搜索法。遍历所有可能的消失点假设，选择最优的消失点集作为检测结果。遍历所有网格单元，选择响应最强的第二和第三个消失点，但穷举搜索的时间复杂度很高。
本文提出的灭点检测方法综合了上述两种方法的优点。为了保证算法的全局最优性，利用两线MSS最小解集估计第一个消失点，并利用消失点的正交性对第一个消失点进行估计。第二个灭点在该点为法线的平面上经过。为了加快穷举搜索的速度，极坐标网格的构造将遍历问题转化为搜索问题，降低了时间复杂度；
（3）在初始化阶段，首先求解图像中的三个正交消失点；将同一消失点对应的结构线分类为一类，并保存每条线段的中点和消失点坐标（图4）。在完成线段匹配后，还可以对中点坐标进行三角化以恢复深度，并且方向由消失点坐标的反投影表示.

5.创新点在哪：

（1）结构线的主导方向（是消失点方向么？）可以提供全局有效的约束，减小累积的方向误差和由此产生的位置漂移；
（2） 在图像中求出消失点的坐标（消失点应满足正交约束），根据每条直线所属的消失点对结构线进行分组，因为消隐点在图像中的位置只与直线的方向有关，与平移无关。将不占主导方向的线段剔除。属于同一主导方向的结构线彼此平行，因此属于同一灭点。

6. 该文章的主要成就（最好使用数据论述）：
（1）TUM的一个6m长度路线的一个数据集：集成结构线特征的算法提高了整体精度。具体而言，总均方根误差从0.028779增加到0.008597;
（2）使相对轨迹误差的总体分布更加平衡（图9）。 ；
（3）大场景60m*40m的olympic4f 数据集：在该结构化场景中检测到的线特征占更多像素

二.文章翻译

1. Introduction忽略
2. Related work
（1）
(Smith 2006)提出了一种基于直线的单目视觉SLAM，在空间上用两个端点表示一条直线，在后端使用EKF框架。在28 s的图像序列测试中，综合考虑点和线，可以取得良好的跟踪效果。

Andrew et al.(2006)也使用两个端点表示一条直线来实现实时SLAM系统。但是，与用两个端点来表示直线特征相比，用无限线段来表示直线更适合大场景下的大规模SLAM。Lemaire(2007)和Sola et al.(2009)的一些作品中提出了这一观点。Bartoli et al.(2005)等人综合利用点线特征构建了基于关键帧后端优化的视觉SLAM系统，克服了图像模糊导致匹配失败的问题。

Pumarola and Zuo均扩展了ORB-SLAM框架，提出了一种点线集成的PL-SLAM (Pumarola 2017)。前者以单目视觉为基础，包含初始词。

后者以双目视觉为基础，将分割的线段进行合并。

然而，线的一个显著缺点是它们往往是不完全检测和部分遮挡，导致系统的不稳定。以往对线特征的研究很少考虑线的平行性、正交性、共面性等结构信息，因此在噪声的影响下，它们比基于点的方法更不稳定，结果也更差。

一些研究人员将非结构点和线结合起来，使系统更适用于一些具有挑战性的场景。Li等人(Li and Yao 2017)设计了一个模型，可以高效地处理点和线，可以应用在具有稀缺特征的极端场景中。

基于双目视觉的SLSLAM (Zhang et al. 2016)方法提出了基于三维直线构造地图的方法。然而，虽然这些方法可以利用更多的观测数据，但它们无法克服上述非结构特征的固有缺陷，并且由于缺乏有效的约束，其精度有限。

基于结构特征的方法考虑结构线索，并经常应用于人造环境，可以抽象为一组共享三个共同主导方向的块。在这种被称为曼哈顿世界的场景中，结构的规律性可以提供有效的几何约束，这有助于提高SLAM的精度。首先，每条三维结构线都平行于三个相互正交的主导方向中的一个。在投影变换下，一组平行的3D线形成一簇投影线，这些投影线在图像中收敛于同一点，称为消失点(VP) (Lu 2017)。

其次，一些三维点和线在同一平面上，它们的法线平行于三个主要方向中的一个。Lee等人(2009)提出了一种将vp作为室内建筑虚拟地标的方法。因为VP在整个场景中都是可见的。Camposeco(2015)使用惯性辅助方法检测副位移，并将副位移集成到视觉测程系统中，以减少角漂移。Zhou等人(2015)提出了一种利用建筑结构线的系统。该系统基于扩展卡尔曼滤波(EKF)框架，能够有效地减少定向误差的累积，并优于现有系统。副元作为结构特征的第一类，反映了机器人的并行性和正交性，常被用于机器人状态估计。作为第二类结构特征，共面点与线与旋转和平移都有关系，而vp只能对旋转施加约束。
Mei提出了一种基于共面点的跟踪映射方法。提出了一种基于共面性的误差最小化方法。Kwon和Lee(2010)提出了一种基于粒子滤波的基于局部平面地标的SLAM框架。但是，这些方法只考虑共面点而不考虑直线，并且忽略了曼哈顿世界中平面固定法线的先验知识，导致在走廊等室内低纹理环境中稳定性较差。其他有关共面性的研究利用了曼哈顿世界的几何先验。Kosecka et al.(2005)提出了一种策略，通过属于同一个VP的线提取主导平面，然后估计相机姿态。
3 . Three‑dimension structure line feature
3.1图像中结构线特征的提取
估计相邻帧之间的位姿变化需要匹配不同视角下的图像特征。因此，良好的特征必须被稳定地检测和很好地区分。线特征主要是图像中的边缘，它是指在一个局部区域中具有相同像素梯度变化方向和相邻位置的一组点。

线特征包含了图像中最基本的几何和拓扑信息。结构线特征也是一种线特征，在曼哈顿世界中，它是主导平面上的一条直线(Coughlan 1999)。

因此，提取结构线特征的前提是检测出图像中所有的直线。传统的线检测方法一般采用边缘检测算法提取二值边缘图像，然后利用Hough变换将表示每条线属性的参数投影到Hough空间中。这种直线检测方法是一种全局拟合算法。缺点是依赖于边缘检测算法的准确性，在边缘密集的地方容易发生异常检测。

本文选择实时LSD (Von 2012)(一种线段检测器)方法作为提取前端线段特征的线段检测算法。LSD算法是基于梯度信息的直线检测方法，检测速度快，参数自适应，精度可达亚像素级。其主要思想是在局部区域内合并具有相同梯度方向的像素，以达到检测直线的目的。

检测到线材后，要根据线材的方向进行分类，不处于主导方向的线材要去除。属于同一主导方向的结构线相互平行，属于同一消失点。消失点就是交点由平行的直线光束经相机模型投影后在成像平面上形成的物理空间。因为消失点在图像中的位置只与直线的方向有关，与平移无关。

因此，如果在图像中求解消失点的坐标，就可以根据每条直线所属的消失点对结构线进行分组。在曼哈顿世界中，消失点提取算法需要满足两个约束条件。首先，计算的消失点应该是全局约束的，而不仅仅是局部最优解。其次，求出的消失点应满足曼哈顿世界假设，即求出的消失点应满足正交约束。

目前的消失点提取算法可以用以下两类算法来表示(Lu 2017):(1)基于ransac的方法。通过定义最小解集，随机选取满足最小解集数解交点的直线作为假设的消失点，然后计算剩余的直线是否满足这个假设。(2)穷举搜索法。遍历所有可能的消失点假设，选择消失点的最佳集合作为检测结果。遍历所有网格单元，选取响应最强的第二、第三消失点，但穷举搜索时间复杂度较高。

本文提出的消失点检测方法结合了上述两种方法的优点。为了保证全局最优，采用2线MSS最小解集估计第一个消失点，并在第一个消失点上利用消失点的正交性。第二个消失点在平面上遍历，这个点是法线。为了加快穷举搜索速度，构建极坐标网格将遍历问题转化为搜索问题，降低了时间复杂度.

上述提取消失点的方法可以说是原封不动的照搬照抄了，参考博客

：PSL‑SLAM:PSL‑SLAM: a monocular SLAM system using points and structure lines in Manh 曼哈顿世界中的点线单目SLAM
3.2三维直线表示
对于环境地图中的特征，除了跟踪其在图像中的位置外，还需要获得其在现实世界中的坐标。特征点的三维参数化可以方便地用世界坐标系中的三维点坐标yi = (Xw, YW, Zw)表示。考虑到三维空间中的一条直线有4个自由度，需要选择合适的参数化方法，这对误差模型的建立和优化规模的复杂性有一定的影响。

在三维空间中，直线可以由通过直线的两点的组合来确定，也可以由两个平面的交点来确定。假设均匀直线上两点的坐标为 [ AT, BT ]（AT代表A的转置）。结合A和B得到W = [AT,BT]T。生成的 W* 子空间可以表示一条直线上的所有点。
同样，一条直线可以由两个平面来确定，假设两个平面坐标的组合是* W * = [ATBT]T。* W的零空间构成了直线上所有点的集合。
但是，这种用零生成空间的子空间表示直线有八个维度，这种表示方法显然是多余的。
在本文中，更紧凑的采摘器坐标(Sola等。
2009)表示和正交表示(Bartoli et al. 2005)被用来参数化空间直线。
Pluck坐标表示是6个自由度的表示，在表示变换和重投影时具有很好的线性特性。假设直线上两点的坐标为AT, BT，Pluck矩阵L可以表示为

L是一个反对称矩阵秩为2且所有对角线元素都为0。L中有很多非零元素。

将Pluck矩阵中的六个非零元素按一定的顺序取出，排列成一个六维向量，用Pluck坐标表示，用L(弯曲，代表罗马文字)表示，L中的v为方向向量，力矩n为平面通过原点和直线的法向量。它垂直于方向向量，需要满足nT（n的转置）v = 0的约束。Pluck矩阵L与Pluck坐标L之间的转换关系如下

其中n⋀表示向量到反对称矩阵的转换。使用Pluck坐标来表示空间中的直线有很多优点。特别是当它表示坐标系转换和相机重投影时，它具有线性形式。例如，将世界坐标系和摄像机坐标系进行转换时，可以表示为

Pluck坐标表示也是一个过度参数化的表达式。用6个参数表示一条直线，而空间直线只有4个自由度。在后续的迭代优化中，额外的参数将被强制满足n和v的正值性（positive）。这将增加后端计算的负担。

Bartoil在文献(Bartoli et al. 2005)中提到了一个四参数最小化的正交表达式(U, W)∈SO(3) × SO(2)，以Plück坐标进行QR分解得到。设Plück坐标为L = [nT vT]T，分解结果为:

QR分解可以分离出正交矩阵U，将其视为从摄像机坐标系到线性坐标系的旋转。

线性坐标系是以垂直脚为原点，n, v, n × v三轴为正交基的坐标系。W表示从原点到直线的距离信息
正交表示，在表示坐标变换时，虽然没有Pluck坐标的线性性质好，但是在迭代求解空间中直线的位置时，它有很好的导数性质。增量可以由切空间中的元素定义。设置增量为
增量参数具有明显的几何意义。θ1调整直线三个轴的旋转。θ2控制从三维直线到原点的垂直距离。迭代过程可以表示为

由于正交表示只有4个自由度，因此在优化过程中不会引入额外的约束，适合于后端优化。然而，在前端视觉里程表中很难表达重投影变换，因此本文仅在后端优化中使用正交表示，在其他情况下使用Plück坐标。
3.3观测模型
观测模型建立了观测数据与已知状态量之间关系的模型。

本文中，观测数据是图像中匹配的特征点线，已知状态量是求解的地标。空间直线的裁剪投影完成后，投影线段往往不能与匹配线段完全重合。两条线段之间的误差称为重投影误差，误差的定义称为观测模型。

线特征的误差形式定义如下
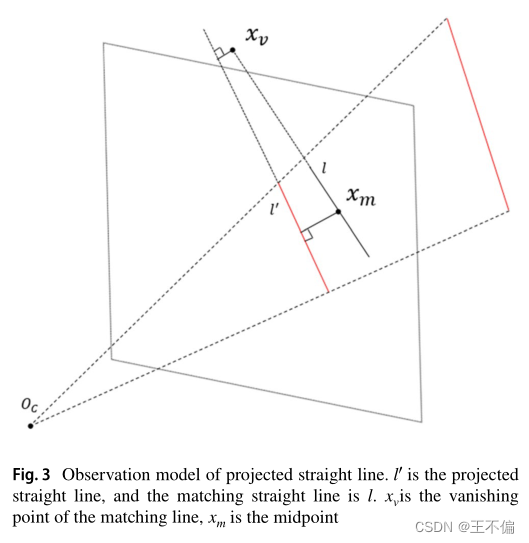
其中，l’= （l1、l2、l3）T、e1表示匹配线段中点到投影线的垂直距离，e2表示匹配线段消失点到投影线的距离，其中xv可能不在中的图像中，但仍可获得坐标。由于检测算法的端点不确定性，垂直于投影线的这部分距离可以提供更丰富的信息，并且每帧中的消失点值相对稳定，因此设计该观测模型是合理的。
4.使用点和结构线的SLAM系统
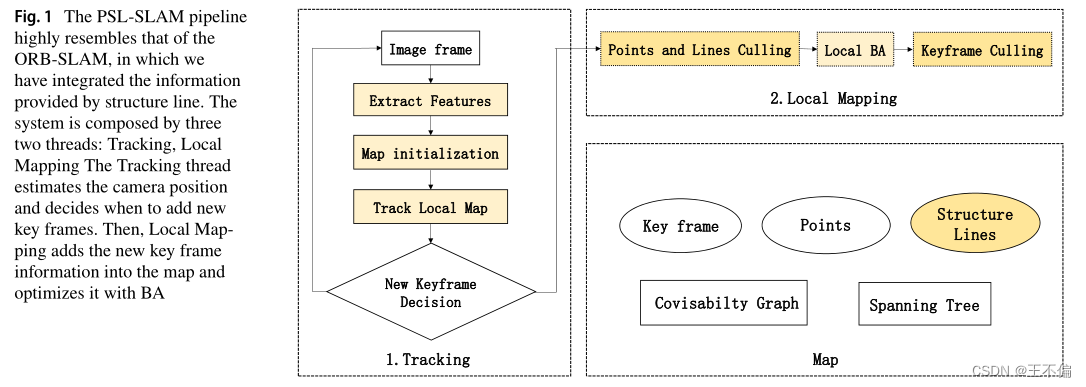
我们的方法与ORB-SLAM非常相似，其中我们集成了结构线特征、改进的跟踪和局部映射提供的信息（见图1）。

PSL-SLAM流程（pipeline）与ORB-SLAM流程（pipeline）非常相似，我们在其中集成了结构线提供的信息。该系统由三个两线程组成：跟踪、局部映射跟踪线程估计摄像机位置并决定何时添加新的关键帧。然后，局部映射将新的关键帧信息添加到映射中，并使用BA对其进行优化

1） 跟踪线程：跟踪线程主要完成前端视觉里程表的工作。

首先，初始化环境地图，获取初始三维地标的初始姿态和深度信息。单目相机通过两个视图几何体恢复场景深度，而双目相机和深度相机可以直接反向投影以获取深度信息。其次，利用特征匹配实现姿态跟踪，分为相邻帧跟踪和局部地图跟踪。通过最小化重投影误差来更新当前帧的姿态，为后端优化提供更好的初始值。

2） 局部映射线程：局部映射线程完成系统状态变量的后端优化。由于通过跟踪线程增量构造贴图的方法不可避免地会产生累积错误，因此我们扩展了包含结构线的局部贴图。通过维护由与当前帧具有共同视图关系的所有关键帧组成的局部贴图，贴图的局部优化问题进一步优化了当前姿势。
4.1与StructVIO和PL-SLAM的讨论StructVIO首先提出了融合结构线以提高SLAM算法性能的方案，我们想强调我们与StructVIO的不同之处。

（1） StructVIO（Zhou et al.2015；Wu et al.2019）基于过滤框架。将测量模型集成到扩展卡尔曼滤波SLAM系统中进行状态估计。（2） 我们改进了消失点提取算法，以满足前两个消失点的正交性。（3） 而不是使用初始关联线段中点周围的图像面片作为描述符，我们使用了一种改进的行匹配算法来消除更多不相关的匹配。

PL-SLAM（Gomez-Ojeda 2017）也是一个通过点和线段组合的SLAM系统。（1） PLSLAM使用直线的两个端点来表示，线段的端点检测具有很强的不确定性。我们使用全局主导方向和线段中点来表示检测的不稳定性降低。（2） PL-SLAM的度量模型不是基于线特征匹配，而是仅使用端点信息进行匹配。相反，我们充分挖掘了结构线的信息，以实现线特征的匹配（图2和图3）。

4.2点匹配和线匹配
特征匹配算法在环境地图的初始化部分和跟踪部分起着重要作用。

稳定跟踪是算法稳定运行的关键，对系统的鲁棒性有很大影响。这在很大程度上取决于特征匹配的准确性。

本文使用ORB特征来检测和描述特征点。对于线特征的匹配部分，首先使用LSD进行线检测，然后在结构线提取后使用LBD（Gomez Ojeda 2017）进行线特征描述。描述符表示特征周围像素的信息。为了减少特征点的不匹配，本文采用了几种策略：（1）基于主旋转方向消除不匹配。计算整个图像的平均旋转。若特征点描述符和整个图像的相对旋转角度相差很大，则认为不匹配。（2） 根据最短距离和第二短距离的比率。如果最短距离与第二短距离的比率大于某个阈值，则认为特征点失败。

（3） 此外，还可以根据极线约束减少特征点的错误匹配。利用匹配点得到基本矩阵后，通过基本矩阵计算出匹配图像上的极线。如果匹配的特征点离极线太远，请跳过匹配。
4.3地图初始化
在视觉里程计中，需要首先完成地图的初始化。视觉SLAM是一种相对定位。

通常，以第一个参考系作为坐标原点，将空间地标的三维坐标恢复为初始地图点，然后根据建立的初始地图进行跟踪和姿态求解。在初始化阶段，本文提出的算法不仅恢复了初始特征点的深度，而且对结构线进行了初始化。

三角剖分可以初始化特征点的三维坐标。对于结构线，还需要获取三维参数表示。在本文中，线的中点和消失点方向用于表示结构线。在初始化阶段，首先求解图像中的三个正交消失点；将同一消失点对应的结构线分类为一类，并保存每条线段的中点和消失点坐标（图4）。

在完成线段匹配后，还可以对中点坐标进行三角化以恢复深度，方向由消失点坐标的反投影表示。假设v是第一帧中结构线的消失点坐标，则消失点方向伊塔η （n带尾巴==η）在世界坐标系中的位置可以表示为：
其中，RWC是相机坐标系到世界坐标系的旋转。η 仅表示结构线的方向，其几何意义表示通过相机光学中心的线性光束η . M是结构线中点对应的三维坐标，结构线可由中点和主导方向确定，Plück矩阵可定义为

4.4 Track Local map
Track Local map是整个线程的核心。在获得初始地图后，可以跟踪空间地标，并将现有的空间点与图像中的匹配特征相关联，即三维到二维的数据关联。PnP算法可以根据匹配点集求解姿态。它描述了已知的三维点{Xi}和匹配的二维点{ui}，如何解决当前帧姿态的外部参数R，t的问题。本文中添加了线要素，需要将点要素和线要素组合在一起。

姿态跟踪主要分为帧间跟踪和局部地图跟踪两部分。帧间跟踪是将前一帧中跟踪到的空间特征与当前帧的匹配特征相关联。首先，使用匀速模型获得初始姿态，然后使用该初始姿态将空间点和线投影到当前帧上。在图像中，从当前帧提取的特征之间存在匹配。

因为姿势是假定的，所以投影的虚线通常不能与匹配的虚线完全重合。

利用重投影误差优化当前姿态并获得局部最优解。

假设在前一帧的空间中观察到一个点Xw=[X Y Z]T和一条空间直线LW。由匀速模型估计的当前帧的初始姿态为Tkw′。投影前，需要判断空间点线是否在当前相机的视野内。留下图像的可观察部分。Xw在图像中的投影为

在结构线的Plück坐标中，Lw的vT=[nT vT]T是消失点的方向。

对消失点进行反投影，可以得到图像中匹配的消失点xv
图像中点的投影点为xm，两点xv和xm可用于确定投影线 l’，其中xv可能不在图像范围内，但仍可获得l’。此时，3D到2D匹配完成。一般的优化框架是：

假设跟踪到的空间点、线坐标准确，当前帧共有i线匹配和i点匹配，以当前帧的姿态Tkw为优化变量，构建一个图模型，使上述代价函数最小化，以获得局部最优解Tkw∗.

帧间跟踪不能很好地保证系统的精度，因为代价函数只包含前后两帧的信息，会产生较大的累积误差，导致轨迹漂移。

针对这个问题，可以增加优化范围，并可以重新投影环境地图中的所有点和线以计算误差。但是，对环境地图中的所有点和线进行投影计算会造成资源浪费。visual SLAM将通过维护局部地图来解决此问题。局部地图描述当前帧所在的环境信息。它包括与当前帧具有相同观测值的所有关键帧（此处的阈值至少为20个相同观测值）以及这些关键帧观测到的空间点和线。这种跟踪方法称为局部地图跟踪。

局部地图跟踪将局部地图中的所有空间点和线投影到当前帧，丢弃图像范围以外的点，并通过地图优化进一步优化当前姿势。与帧间跟踪相比，局部地图跟踪仍然使用当前帧的姿态Tkw作为优化变量来构建图模型。不同的是，误差部分成为局部地图中所有空间点和线的投影误差，匹配点的数量增加。较大的匹配范围可以估计更精确的姿势。

4.5新关键帧决策
跟踪线程获得初始姿势后，需要将其输入到局部映射线程中，以进一步计算更精确的姿势。但是，如果输入了所有历史力矩的初始姿势，则计算量太大。此外，实时的帧数采集的图像序列太多，可以认为相邻帧之间的运动状态相差不大。通常，只能选择轨迹中的特定帧作为关键帧组成的局部映射，然后进一步优化局部映射中的帧。关键帧的选择会影响系统对齐的精度。如果选择的关键帧过于密集，将导致信息冗余，如果过于稀疏，则很容易导致跟踪失败。

在本文中，使用以下三个条件来确定当前帧是否用作关键帧（1）自上次插入关键帧以来已通过20帧或本地地图线程处于空闲状态（2）当前帧跟踪至少50个特征点和15条直线。（3） 当前帧必须有一定的视觉变化对于其他关键帧的所有特征，共同观察特征的比例需要小于75%。

4.6为当前帧创建局部地图
在处理新到达的关键帧时，创建当前帧的局部映射，首先使用当前帧与其他关键帧之间的公共视图关系来建立当前关键帧的局部映射。公共视图关系是指在两个关键帧之间共同观察到的地图点和线的数量。首先，从当前关键帧中取出常用的关键帧，统计常用观测值的数量并进行排序。其次，将这些具有共同观测的关键帧及其观测到的所有地图点和线添加到局部地图中。

4.7点和结构线的束平差（BA）
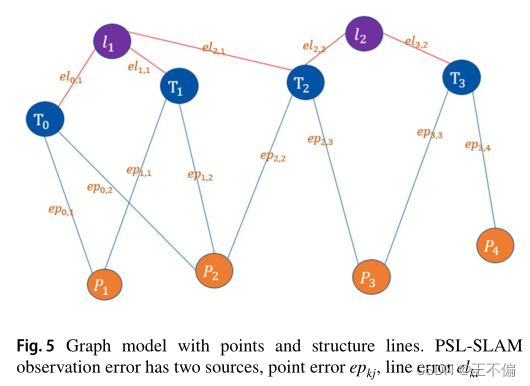
如图5所示，图优化理论可以将非线性优化问题构造为图模型，将变量抽象为图结构中的顶点，将误差项构造为连接顶点的边，并添加线特征以相应地增加图（见图5）。

点误差模型定义如下。假设当前帧的初始姿势为TC，W。某一地标点的空间坐标为XW，利用初始姿态将XW投影到摄像机坐标系中得到XC，然后计算投影到图像中后投影点坐标x′与匹配点坐标x之间的距离，得到点误差epkj。
TUM数据集中freiburg3\u structure\u texture\u far序列的图像。这组数据是沿着用木板搭建的结构化场景收集的。木板用锡箔纸包裹，几张彩色海报水平地放在前面的地板上


第四章阐述了结构线特征的观测模型。通过在总体成本函数中加入结构线的误差elki，可以合并特征点和结构线特征的信息。然后，综合误差的成本函数可以写为：

代价函数的最优解等价于状态量的极大似然估计，代价函数不是一般的线性函数，用一般的求导方法无法直接求出代价函数的极值。有必要使用非线性优化问题的最小值。这需要推导每个状态量的雅可比矩阵（图6）。

线特征误差与状态量有关，状态量是相机姿态TC、W和线特征空间坐标的正交表示LW。因此，LW也可以解决。

以增量Δθ迭代。根据链推导规则：
首先，从相对于投影线LW的线特征误差的雅可比矩阵开始，假设 l’ = （l1，l2，l3）T，匹配线消失点值的齐次坐标为xv=（uv，uv，1）T，中点值xm=（um，um，1）T的齐次坐标。el 在投影线上的雅可比矩阵形式可以导出：
投影线l′的雅可比矩阵部分可以写成

L’c对相机姿态的推导更为复杂，它可以分解为两部分：旋转和平移。首先，对于旋转，设置平移部分δp到0，然后δξ= [ δφ，0]T。首先给出Lc的形式 仅通过旋转进行更改：
对于平移部分的偏导数，假设旋转部分的李代数ξ为0，δξ= [ δφ，0]T，Lc和 Lw之间的映射关系根据上述推导得出：
由于Rcw与平移部分的增量无关，因此可以获得平移部分的偏导数：
5实验结果
我们使用TUM RGB-D基准将我们的系统与当前最先进的视觉SLAM方法进行了比较。所有实验均使用Intel core i5-5200U（@2.2GHZ）8Gb RAM和ROS Hydro进行。

本文提出的算法主要针对结构化场景进行了改进。因此，选择TUM数据集中的freiburg3\u structure\u texture\u far序列进行对比实验分析。
这组数据是沿着用木板搭建的结构化场景收集的。木板用锡箔纸包裹，几张彩色海报水平放置在前面的地板上。该数据集的视频总长度为31.56秒，图片序列中共有907帧，真值文件的轨道长度为5.884米。

为了将该算法估计的轨迹与提供的真实轨迹进行比较，需要对齐两个参考坐标系。该方法以第一帧的姿态作为参考帧初始化姿态估计，而实际轨迹则以固定的世界坐标为参考。以对齐两个参考系统（图7）。

假设第一帧用作转换参考，则实际轨迹第一帧的姿态设置为TG1，估计的姿态为I。然后，两个参考系的变换矩阵T应为：

发现仅从一帧计算的变换矩阵T具有较大的误差，因为第一帧可能有噪声，则应考虑所有帧的姿态来构造最小二乘问题。因此，假设估计姿态的3D点集为P，实际轨迹的3D点集为P’，
该最小二乘问题可以构造为
对准参考坐标系后，比较ORB-SLAM和我们的PSL-SLAM在数据集上估计的轨迹。这两种算法都使用相同的特征点参数来提取特征，即每帧图像在八个比例空间中总共提取1000个特征点，比例因子为1.2。如图8所示，ORB-SLAM算法和PSL-SLAM在该数据集上取得了很好的结果，很难从视觉上看到差异。这主要是因为在小场景中，误差积累情况不明显，数据集具有丰富的点和线特征，移动缓慢，抖动弱。为了更准确地测量两种算法的误差，我们还使用了绝对位姿误差（APE）进行评估。从图8和表1可以看出，集成结构线特征的算法提高了整体精度。具体而言，总均方根误差从0.028779增加到0.008597。最大定位误差和最小定位误差都得到了改善。此外，ORB-SLAM的误差在帧间累积，导致后期漂移增加。我们的方法不仅降低了误差水平，但也使相对弹道误差的总体分布更加平衡（图9）。

为了验证该算法在大规模室内场景中的性能，本文在olympic4f数据集上进行了实验。数据集的主要主题是室内大型走廊场景。该场景具有丰富的点和线特征。

难点在于场景范围太大，走廊长度约为60×40m，且容易累积轨迹漂移。该数据集包含9506帧消除失真的灰度图像序列。其中，手持式摄像机拍摄时存在光照变化和一定程度抖动的场景，这也增加了点特征稳定跟踪的难度。我们在这个数据集上测试了我们的方法的实时性能，如图10所示。当前帧的匹配点和线特征显示在右侧图像上。点特征是亮度发生显著变化的角点。线特征主要是对象的边缘，例如图像中墙柱、门框和瓷砖的边缘。从图10可以看出，在该结构化场景中检测到的线特征占更多像素。

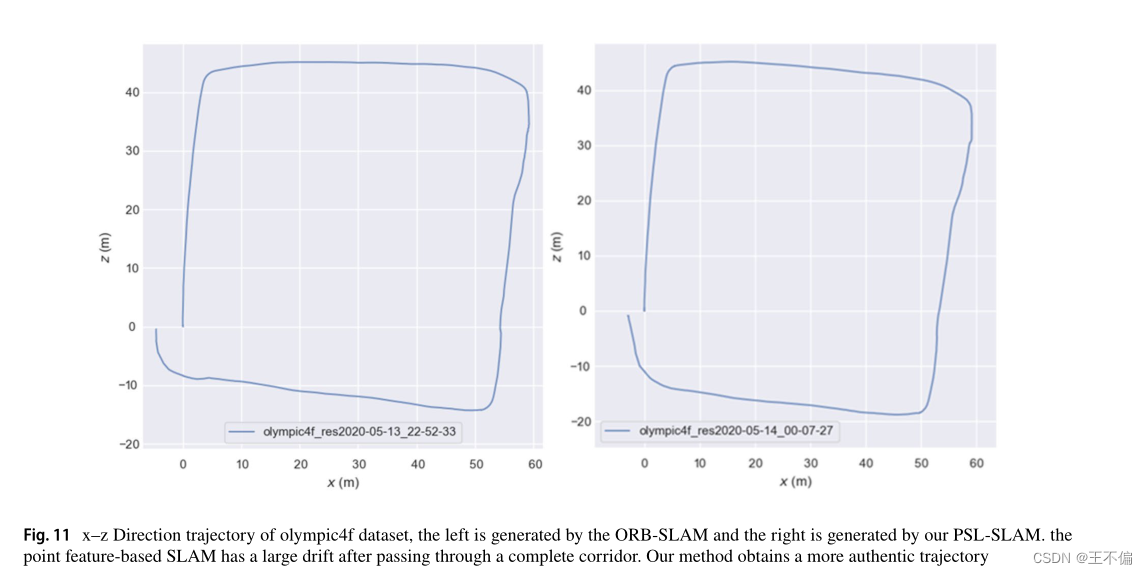
在这个公共数据集上，我们还使用相同的参数进行了点特征提取的对比实验，获得轨迹文件后，使用Evo工具可视化轨迹。如图11所示，基于点特征的SLAM在通过一条完整的道路后具有较大的曲线。算法的运动轨迹本文有效地减少了累积误差，获得了更真实的轨迹。

为了验证算法的性能，我们在真实场景中进行了实验。如图12所示，我们选择了学校的室内走廊场景。场景有一个四个角的矩形环。结构化场景线特征比较丰富，结构线较多。某些角点是低纹理区域。

例如，第三个角点很难定位。本实验收集该场景的图像数据，并使用本文对ORB-SLAM和改进算法进行了对比实验分析。

为了稳定采集数据，避免手持式摄像机的抖动，本文搭建了移动机器人数据采集平台进行数据采集。硬件平台主要由Turbot移动机器人底盘和Kinect摄像头组成。底盘底部安装四个独立的麦卡努姆轮，实现机器人的全方位运动，方向可由手柄控制。在本实验中，首先用一个手柄控制机器人沿着物体的中心移动以恒定的速度在走廊上录制视频，然后使用保存的数据集对本文提出的视觉定位系统进行实验。该实验以30帧1秒的帧速率采集6480帧图像数据，分辨率为640×480（图13）。

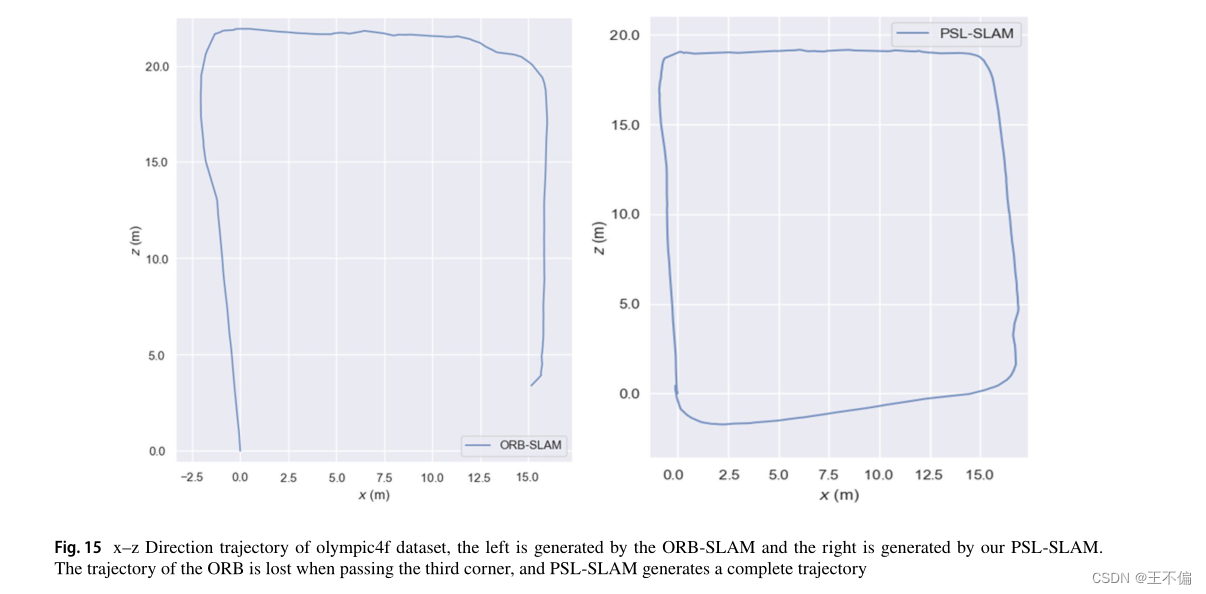
从图14可以看出，ORB-SLAM算法中当前帧的特征点跟踪丢失，并且没有成功匹配的特征点。跑步轨迹在穿过低纹理区域的第三个拐角处丢失，轨迹和贴图的生成停止。可能的原因是角点纹理较少，且特征点匹配导致数据关联失败的故障。同时，本文提出的算法已经处理到了图像输入序列的末尾，并生成了完整的运行轨迹。图像中跟踪的结构线特征丰富，角点后轨迹不会丢失，局部地图中包含的地标点不断生成，当前关键帧姿态也得到稳步优化。通过这一部分的实验可以得出结论，在加入结构线后，本文的算法可以有效地增强帧间的跟踪和匹配效果，使得算法更适合室内复杂场景，提高鲁棒性（图15）。

结论
曼哈顿世界编码中的结构特征提供了场景中平行、正交和/或共面的有用几何信息。通过充分利用这些结构特征，我们提出了一种新的单目SLAM系统，它可以提供更精确的相机姿态估计。该系统的最大贡献是基于结构特征的优化模块，该模块包含点和结构线特征优化策略。首先，利用结构线方向与消失点方向的一致性来提取结构线。在优化模块中，我们将结构线的误差模型引入到非线性优化框架中，并提出了一种新的优化策略。最后，设计了一个完整的基于点和结构线的SLAM系统。

与非结构特征相比，我们提出的系统充分利用结构约束来减少累积的方向误差和由此产生的位置漂移。并利用VPs所反映的平行性和正交性来优化旋转。在人造环境中的实验表明，该系统在精度和鲁棒性方面优于现有的最先进的单目SLAM系统。

今天的文章PSL‑SLAM:PSL‑SLAM: a monocular SLAM system using points and structure lines in Manh 曼哈顿世界中的点线单目SLAM分享到此就结束了，感谢您的阅读。