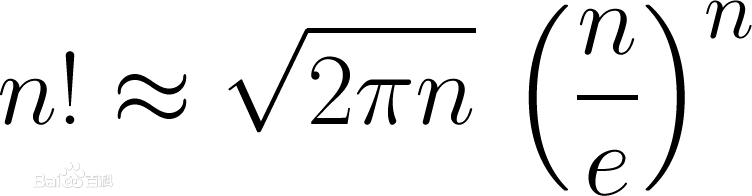斯特灵定理_代数公式

（ 数论专题 ）【斯特灵公式】

斯特林公式是一条用来取n的阶乘的近似值的数学公式

一般来说，阶乘的计算复杂度为线性。当要为某些极大大的n求阶乘时，常见的方法复杂度不可接受。斯特林公式能够将求解阶乘的复杂度降低到对数级。而且，即使在n很小的时候，斯特林公式的取值已经十分准确。

斯特林公式可以用来估算某数阶乘的大小，结合lg可以估算某数的阶乘的位数，或者可以估算某数的阶乘是另一个数的倍数。

给你一个整数n，求n！的位数。利用斯特灵公式求解n!的位数：

易知整数n的位数为[lgn]+1（ 证明：用科学计数法表示数n为1.xx * 10^k , 对这个数取对数就是k+log10(1.xx), 大约就是k+1位 ）。.利用Stirling公式计算n!结果的位数时，可以两边取对数，得:

log10(n!) = log10(2*n*Pi)/2+n*log10(n/e)

则答案为：   ans = log10(2*n*Pi)/2+n*log10(n/e) + 1

#include<bits/stdc++.h> using namespace std; const double pi = acos(-1); const double e = exp(1); signed main() { int n;cin>>n; int w=1; for ( int i=1; i<=n; i++ ) w*=i; cout << w << endl; // cout << sqrt(2*acos(-1)*n)*pow(1.0*n/exp(1),n); // 输出n!的Stirling值 cout << int( log10(2*pi*n)/2+n*log10(1.0*n/e) ) + 1 << endl; // 输出n!的位数 return 0; }

今天的文章
斯特灵定理_代数公式分享到此就结束了，感谢您的阅读。