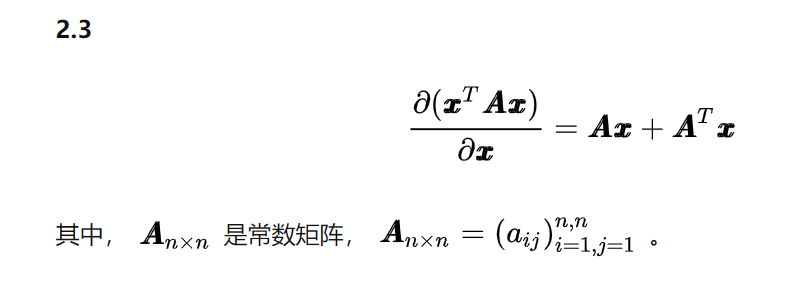基础原理
最小二乘法,也称最小平方法,即计算误差平方和最小,得到的最佳估计。
核心问题:最小二乘估计的合理性证明是什么? 数学王子高斯(1777-1855)也像我们一样心存怀疑。高斯随后通过概率论的理论证明了最小二乘法的合理性。
参考文献
最小二乘法的递推形式推导
最小二乘法的本质是什么
最小二乘法的几何意义
矩阵形式的最小二乘法
矩阵求导公式的推导
实值函数相对于向量的梯度
理论公式
最简单的最小二乘法
单参数的观测与估计:
误差的平方和: S ϵ 2 = ∑ ( y − y i ) 2 \text{误差的平方和:}S_{\epsilon ^2}=\sum{\left( y-y_i \right) ^2} 误差的平方和:Sϵ2=∑(y−yi)2
法国数学家勒让德表示:总误差平方和最小时,y值即为最佳估计。
d S ϵ 2 d y = d d t ∑ ( y − y i ) 2 = 2 ∑ ( y − y i ) \frac{dS_{\epsilon ^2}}{dy}=\frac{d}{dt}\sum{\left( y-y_i \right) ^2}=2\sum{\left( y-y_i \right)} dydSϵ2=dtd∑(y−yi)2=2∑(y−yi)
当i最大为5时,可得:
2 ∑ ( y − y i ) = 0 ( y − y 1 ) + ( y − y 2 ) + ( y − y 3 ) + ( y − y 4 ) + ( y − y 5 ) = 0 y = y 1 + y 2 + y 3 + y 4 + y 5 5 2\sum{\left( y-y_i \right)}=0 \\ \left( y-y_1 \right) +\left( y-y_2 \right) +\left( y-y_3 \right) +\left( y-y_4 \right) +\left( y-y_5 \right) =0 \\ y=\frac{y_1+y_2+y_3+y_4+y_5}{5} 2∑(y−yi)=0(y−y1)+(y−y2)+(y−y3)+(y−y4)+(y−y5)=0y=5y1+y2+y3+y4+y5
当估计的对象为一个一元一次函数时,设估计对象函数为:
y ( x ) = a x + b y\left( x \right) =ax+b y(x)=ax+b
若已知测量点(xi,yi),则最小二乘误差为:
S ϵ 2 = ∑ ( a x i + b − y i ) 2 S_{\epsilon ^2}=\sum{\left( ax_i+b-y_i \right) ^2} Sϵ2=∑(axi+b−yi)2
不同的a,b参数会导致不同的误差平方和,即误差平方和是a,b的函数。
计算偏导数为0可得:
{ ∂ S ϵ 2 ∂ a = 2 ∑ ( a x i + b − y i ) x i = 0 ∂ S ϵ 2 ∂ b = 2 ∑ ( a x i + b − y i ) = 0 \begin{cases} \frac{\partial S_{\epsilon ^2}}{\partial a}=2\sum{\left( ax_i+b-y_i \right) x_i=0}\\ \frac{\partial S_{\epsilon ^2}}{\partial b}=2\sum{\left( ax_i+b-y_i \right) =0}\\ \end{cases} {
∂a∂Sϵ2=2∑(axi+b−yi)xi=0∂b∂Sϵ2=2∑(axi+b−yi)=0
求解该线性方程组可得a,b得最佳估值。
对于不同得函数关系,对于2,3,4等多参数得估计方法是类似的.
矩阵形式的最小二乘算法
A x ⃗ = F ⃗ 其中 x ⃗ 为代求参数; A 为输入自变量的采样值; F ⃗ 为观测输出值 根据最小二乘原理,使得误差平方和最小的解为估计参数 x ⃗ min ε = ∣ A x ⃗ − F ⃗ ∣ 2 ( 相当于自身的点积 ) min ε = ( A x ⃗ − F ⃗ ) T ( A x ⃗ − F ⃗ ) min ε = ( x ⃗ T A T − F ⃗ T ) ( A x ⃗ − F ⃗ ) min ε = x ⃗ T A T A x ⃗ − F ⃗ T A x ⃗ − x ⃗ T A T F ⃗ + F ⃗ T F ⃗ 上式中:每项的计算结果为标量, F ⃗ T A x ⃗ 与 x ⃗ T A T F ⃗ 互为转置。 根据矩阵运算性质可知: F ⃗ T A x ⃗ = x ⃗ T A T F ⃗ min ε = x ⃗ T A T A x ⃗ − 2 F ⃗ T A x ⃗ + F ⃗ T F ⃗ ε 对 x ⃗ 的每一个元素求导,可以得到 n 个偏导数,令这些偏导为 0 , 得到的 x ⃗ 即为估计值。 计算实值标量函数 ε ( x ⃗ ) 对估测向量 x ⃗ 偏导矩阵: 计算的结果为列向量: ∂ ε ∂ x ⃗ = ∂ ( x ⃗ T A T A x ⃗ − 2 F ⃗ T A x ⃗ ) ∂ x ⃗ = 0 ⃗ A\vec{x}=\vec{F} \\ \text{其中}\vec{x}\text{为代求参数;}A\text{为输入自变量的采样值;}\vec{F}\text{为观测输出值} \\ \text{根据最小二乘原理,使得误差平方和最小的解为估计参数}\vec{x} \\ \min \varepsilon =\left| A\vec{x}-\vec{F} \right|^2\left( \text{相当于自身的点积} \right) \\ \min \varepsilon =\left( A\vec{x}-\vec{F} \right) ^T\left( A\vec{x}-\vec{F} \right) \\ \min \varepsilon =\left( \vec{x}^TA^T-\vec{F}^T \right) \left( A\vec{x}-\vec{F} \right) \\ \min \varepsilon =\vec{x}^TA^TA\vec{x}-\vec{F}^TA\vec{x}-\vec{x}^TA^T\vec{F}+\vec{F}^T\vec{F} \\ \text{上式中:每项的计算结果为标量,}\vec{F}^TA\vec{x}\text{与}\vec{x}^TA^T\vec{F}\text{互为转置。} \\ \text{根据矩阵运算性质可知:}\vec{F}^TA\vec{x}=\vec{x}^TA^T\vec{F} \\ \min \varepsilon =\vec{x}^TA^TA\vec{x}-2\vec{F}^TA\vec{x}+\vec{F}^T\vec{F} \\ \varepsilon \text{对}\vec{x}\text{的每一个元素求导,可以得到}n\text{个偏导数,令这些偏导为}0\text{,} \\ \text{得到的}\vec{x}\text{即为估计值。} \\ \text{计算实值标量函数}\varepsilon \left( \vec{x} \right) \text{对估测向量}\vec{x}\text{偏导矩阵:} \\ \text{计算的结果为列向量:} \\ \frac{\partial \varepsilon}{\partial \vec{x}}=\frac{\partial \left( \vec{x}^TA^TA\vec{x}-2\vec{F}^TA\vec{x} \right)}{\partial \vec{x}}=\vec{0} \\ \\ Ax=F其中x为代求参数;A为输入自变量的采样值;F为观测输出值根据最小二乘原理,使得误差平方和最小的解为估计参数xminε=
Ax−F
2(相当于自身的点积)minε=(Ax−F)T(Ax−F)minε=(xTAT−FT)(Ax−F)minε=xTATAx−FTAx−xTATF+FTF上式中:每项的计算结果为标量,FTAx与xTATF互为转置。根据矩阵运算性质可知:FTAx=xTATFminε=xTATAx−2FTAx+FTFε对x的每一个元素求导,可以得到n个偏导数,令这些偏导为0,得到的x即为估计值。计算实值标量函数ε(x)对估测向量x偏导矩阵:计算的结果为列向量:∂x∂ε=∂x∂(xTATAx−2FTAx)=0
应用矩阵求导的性质:
因此可得:
2 A T A x ⃗ − 2 F ⃗ T A = 0 ⃗ 2A^TA\vec{x}-2\vec{F}^TA=\vec{0} 2ATAx−2FTA=0
简化可得:
x ⃗ = ( A T A ) − 1 F ⃗ T A \vec{x}=\left( A^TA \right) ^{-1}\vec{F}^TA x=(ATA)−1FTA
上式即矩阵形式的最小二乘法的表达式。
对矩阵求导的证明:
∂ ( x ⃗ T A T A x ⃗ ) ∂ x ⃗ \frac{\partial \left( \vec{x}^TA^TA\vec{x} \right)}{\partial \vec{x}} ∂x∂(xTATAx)
对实值标量函数对向量求导的证明: 设: x ⃗ = [ x 1 x 2 . . . x n ] , A = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . . . . a m 1 a m 2 . . . a m n ] , A = A T F ⃗ = [ F 1 F 1 . . . F n ] \text{对实值标量函数对向量求导的证明:} \\ \text{设:}\vec{x}=\left[ \begin{array}{l} x_1\\ x_2\\ …\\ x_n\\ \end{array} \right] ,A=\left[ \begin{matrix} a_{11}& a_{12}& …& a_{1n}\\ a_{21}& a_{22}& …& a_{2n}\\ …& …& …& …\\ a_{m1}& a_{m2}& …& a_{mn}\\ \end{matrix} \right] ,A=A^T \\ \vec{F}=\left[ \begin{array}{l} F_1\\ F_1\\ …\\ F_n\\ \end{array} \right] 对实值标量函数对向量求导的证明:设:x=
x1x2…xn
,A=
a11a21…am1a12a22…am2…………a1na2n…amn
,A=ATF=
F1F1…Fn
x ⃗ T A T A x ⃗ = [ x 1 . . . x n ] [ a 11 a 21 . . . a m 1 a 12 a 22 . . . a 2 n . . . . . . . . . . . . a 1 n . . . . . . a m n ] [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . . . . a m 1 a m 2 . . . a m n ] [ x 1 x 2 . . . x n ] 不妨设 A T A = B x ⃗ T A T A x ⃗ = [ x 1 . . . x n ] [ b 11 b 21 . . . b 1 n b 21 b 22 . . . b 2 n . . . . . . . . . . . . b n 1 . . . . . . b n n ] [ x 1 x 2 . . . x n ] x ⃗ T A T A x ⃗ = ( b 11 x 1 x 1 + b 21 x 2 x 1 + . . . + b n 1 x n x 1 ) + ( b 12 x 1 x 2 + b 22 x 2 x 2 + . . . + b n 2 x n x 2 ) + . . . + ( b n 1 x 1 x n + b 2 n x 2 x n + . . . + b n n x n x n ) ∂ ( x ⃗ T A T A x ⃗ ) ∂ x ⃗ = [ ( b 11 x 1 + b 21 x 2 + . . . + b n 1 x n ) + b 11 x 1 + b 12 x 2 + . . . b n 1 x n . . . . . . ( b n 1 x 1 + b n 2 x 2 + . . . + b n n x n ) + b n 1 x 1 + b 2 n x 2 + . . . b n n x n ] = B x ⃗ + B T x ⃗ \vec{x}^TA^TA\vec{x}=\left[ \begin{matrix} x_1& …& x_n\\ \end{matrix} \right] \left[ \begin{matrix} a_{11}& a_{21}& …& a_{m1}\\ a_{12}& a_{22}& …& a_{2n}\\ …& …& …& …\\ a_{1n}& …& …& a_{mn}\\ \end{matrix} \right] \left[ \begin{matrix} a_{11}& a_{12}& …& a_{1n}\\ a_{21}& a_{22}& …& a_{2n}\\ …& …& …& …\\ a_{m1}& a_{m2}& …& a_{mn}\\ \end{matrix} \right] \left[ \begin{array}{l} x_1\\ x_2\\ …\\ x_n\\ \end{array} \right] \\ \text{不妨设}A^TA=B \\ \vec{x}^TA^TA\vec{x}=\left[ \begin{matrix} x_1& …& x_n\\ \end{matrix} \right] \left[ \begin{matrix} b_{11}& b_{21}& …& b_{1n}\\ b_{21}& b_{22}& …& b_{2n}\\ …& …& …& …\\ b_{n1}& …& …& b_{nn}\\ \end{matrix} \right] \left[ \begin{array}{l} x_1\\ x_2\\ …\\ x_n\\ \end{array} \right] \\ \vec{x}^TA^TA\vec{x}=\left( b_{11}x_1x_1+b_{21}x_2x_1+…+b_{n1}x_nx_1 \right) +\left( b_{12}x_1x_2+b_{22}x_2x_2+…+b_{n2}x_nx_2 \right) +…+\left( b_{n1}x_1x_n+b_{2n}x_2x_n+…+b_{nn}x_nx_n \right) \\ \frac{\partial \left( \vec{x}^TA^TA\vec{x} \right)}{\partial \vec{x}}=\left[ \begin{array}{c} \left( b_{11}x_1+b_{21}x_2+…+b_{n1}x_n \right) +b_{11}x_1+b_{12}x_2+…b_{n1}x_n\\ …\\ …\\ \left( b_{n1}x_1+b_{n2}x_2+…+b_{nn}x_n \right) +b_{n1}x_1+b_{2n}x_2+…b_{nn}x_n\\ \end{array} \right] =B\vec{x}+B^T\vec{x} xTATAx=[x1…xn]
a11a12…a1na21a22………………am1a2n…amn
a11a21…am1a12a22…am2…………a1na2n…amn
x1x2…xn
不妨设ATA=BxTATAx=[x1…xn]
b11b21…bn1b21b22………………b1nb2n…bnn
x1x2…xn
xTATAx=(b11x1x1+b21x2x1+…+bn1xnx1)+(b12x1x2+b22x2x2+…+bn2xnx2)+…+(bn1x1xn+b2nx2xn+…+bnnxnxn)∂x∂(xTATAx)=
(b11x1+b21x2+…+bn1xn)+b11x1+b12x2+…bn1xn……(bn1x1+bn2x2+…+bnnxn)+bn1x1+b2nx2+…bnnxn
=Bx+BTx
由于 B = B T 因此: ∂ ( x ⃗ T A T A x ⃗ ) ∂ x ⃗ = 2 A T A x ⃗ \text{由于}B=B^T \\ \text{因此:} \\ \frac{\partial \left( \vec{x}^TA^TA\vec{x} \right)}{\partial \vec{x}}=2A^TA\vec{x} 由于B=BT因此:∂x∂(xTATAx)=2ATAx
递推形式的最小二乘法
参考“朽木为萤”的推导链接, 由于矩阵形式的最小二乘法是建立在全部测量数据已知的情况进行的计算,若想实现测量数据的同时,实现对真值的最小二乘估计则需要用到递推形式,已知k-1时刻的估计值 x ^ k − 1 \hat{x}_{k-1} x^k−1,和k时刻的量侧 y k y_k yk,实现估计 x ^ k \hat{x}_{k} x^k。k时刻的观测数据获得下式:
y k = H k x + ν k y_k=H_kx+\nu _k yk=Hkx+νk
k时刻的估计和 x ^ k − 1 \hat{x}_{k-1} x^k−1以及 y k y_k yk的关系为:
x ^ k = x ^ k − 1 + K k ( y k − H k x ^ k − 1 ) \hat{x}_k=\hat{x}_{k-1}+K_k\left( y_k-H_k\hat{x}_{k-1} \right) x^k=x^k−1+Kk(yk−Hkx^k−1)
括号里是 x k x_k xk的估计修正, K k K_k Kk是修正增益,以最简单的无偏估计为例,即: E ( x − x ^ ) = 0 E\left( x-\hat{x} \right) =0 E(x−x^)=0
即:
E ( x − x ^ k ) = E [ x − x ^ k − 1 − K k ( H k x + ν k − H k x ^ k − 1 ) ] E ( x − x ^ k ) = E [ ε k − 1 − K k H k ε k − 1 − K k ν k ] E ( x − x ^ k ) = ( I − K k H k ) E [ ε k − 1 ] − K k E [ ν k ] E\left( x-\hat{x}_k \right) =E\left[ x-\hat{x}_{k-1}-K_k\left( H_kx+\nu _k-H_k\hat{x}_{k-1} \right) \right] \\ E\left( x-\hat{x}_k \right) =E\left[ \varepsilon _{k-1}-K_kH_k\varepsilon _{k-1}-K_k\nu _k \right] \\ E\left( x-\hat{x}_k \right) =\left( I-K_kH_k \right) E\left[ \varepsilon _{k-1} \right] -K_kE\left[ \nu _k \right] E(x−x^k)=E[x−x^k−1−Kk(Hkx+νk−Hkx^k−1)]E(x−x^k)=E[εk−1−KkHkεk−1−Kkνk]E(x−x^k)=(I−KkHk)E[εk−1]−KkE[νk]
对于一般情况,即有偏估计情况下,递推最小二乘的最优准则是:使k时刻估计误差方差之和最小,数学表述为:
J k = E [ ( x 1 − x ^ 1 ) 2 ] + E [ ( x 2 − x ^ 2 ) 2 ] + . . . + E [ ( x n − x ^ n ) 2 ] = E [ ε x 1. k 2 + ε x 2. k 2 + . . . + ε x n . k 2 ] = E [ T r ( ε k ε k T ) ] = T r P k 展开 P k , P k = E [ ε k ε k T ] P k = ( I − K k H k ) P k − 1 ( I − K k H k ) T + K k R [ ν k ] K k T 根据上文计算的矩阵求导公式可得: ∂ J k ∂ K k = 2 ( I − K k H k ) P k − 1 ( − H k ) + 2 K k R k 令上式为 0 可得修正系数计算公式: 0 = 2 ( I − K k H k ) P k − 1 ( − H k T ) + 2 K k R k ( I − K k H k ) P k − 1 H k T = K k R k K k = P k − 1 H k T ( R k + H k P k − 1 H k T ) T J_k=E\left[ \left( x_1-\hat{x}_1 \right) ^2 \right] +E\left[ \left( x_2-\hat{x}_2 \right) ^2 \right] +…+E\left[ \left( x_n-\hat{x}_n \right) ^2 \right] \\ =E\left[ \varepsilon _{x1.k}^{2}+\varepsilon _{x2.k}^{2}+…+\varepsilon _{xn.k}^{2} \right] \\ =E\left[ T_r\left( \varepsilon _k\varepsilon _{k}^{T} \right) \right] \\ =T_rP_k \\ \text{展开}P_k\text{,} \\ P_k=E\left[ \varepsilon _k\varepsilon _{k}^{T} \right] \\ P_k=\left( I-K_kH_k \right) P_{k-1}\left( I-K_kH_k \right) ^T+K_kR\left[ \nu _k \right] K_{k}^{T} \\ \text{根据上文计算的矩阵求导公式可得:} \\ \frac{\partial J_k}{\partial K_k}=2\left( I-K_kH_k \right) P_{k-1}\left( -H_k \right) +2K_kR_k \\ \text{令上式为}0\text{可得修正系数计算公式:} \\ 0=2\left( I-K_kH_k \right) P_{k-1}\left( -H_{k}^{T} \right) +2K_kR_k \\ \left( I-K_kH_k \right) P_{k-1}H_{k}^{T}=K_kR_k \\ K_k=P_{k-1}H_{k}^{T}\left( R_k+H_kP_{k-1}H_{k}^{T} \right) ^T Jk=E[(x1−x^1)2]+E[(x2−x^2)2]+…+E[(xn−x^n)2]=E[εx1.k2+εx2.k2+…+εxn.k2]=E[Tr(εkεkT)]=TrPk展开Pk,Pk=E[εkεkT]Pk=(I−KkHk)Pk−1(I−KkHk)T+KkR[νk]KkT根据上文计算的矩阵求导公式可得:∂Kk∂Jk=2(I−KkHk)Pk−1(−Hk)+2KkRk令上式为0可得修正系数计算公式:0=2(I−KkHk)Pk−1(−HkT)+2KkRk(I−KkHk)Pk−1HkT=KkRkKk=Pk−1HkT(Rk+HkPk−1HkT)T
因此可得递归最小二乘估计的步骤:
计算增益:
K k = P k − 1 H k T ( R k + H k P k − 1 H k T ) T K_k=P_{k-1}H_{k}^{T}\left( R_k+H_kP_{k-1}H_{k}^{T} \right) ^T Kk=Pk−1HkT(Rk+HkPk−1HkT)T
估计值更新:
x ^ k = x ^ k − 1 + K k ( y k − H k x ^ k − 1 ) \hat{x}_k=\hat{x}_{k-1}+K_k\left( y_k-H_k\hat{x}_{k-1} \right) x^k=x^k−1+Kk(yk−Hkx^k−1)
协方差更新:
P k = ( I − K k H k ) P k − 1 ( I − K k H k ) T + K k R [ ν k ] K k T P_k=\left( I-K_kH_k \right) P_{k-1}\left( I-K_kH_k \right) ^T+K_kR\left[ \nu _k \right] K_{k}^{T} Pk=(I−KkHk)Pk−1(I−KkHk)T+KkR[νk]KkT
应用方法
知识补充
- 概率密度函数:
- 似然函数?
- 最大似然估计?
今天的文章递归最小二乘算法(原理篇)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/61394.html