自动驾驶 4-5 自行车模型的横向动力学 Lateral Dynamics of Bicycle Model

axle:车轴
lump:集中的
road inclination:斜坡

lateral: 侧面的
vehicle mass:车辆质量
yaw rate:角速度
rear tire:后轮胎
vehicle inertia:汽车惯量

stiffness:刚度

substitue: 替换

在上一堂课中 我们介绍了车辆的动态动态。 下一课中，我们将介绍车辆动态动态 自行车建模方法的四轮汽车的。

在这个视频结束后 你将能够： 使用自行车模型作为起点建立汽车的动态模型， 并以适当的横向控制设计的状态空间进行显示。 让我们开始吧。

我们想扩展我们的运动自行车模型 到动态模型，通过停止运动模型的无运动条件和力。

回想一下, 在全动态自行车模型, 我们保持运动的两个组成部分：第一 在纵向方向上的方向， 第二个在横向方向上垂直于视图。

具体来说，对于横向模型， 我们可能是车辆的旋转速度的模型 基于在移动时影响的矢量特性。

为了开始模拟自行车模型的横向动力学， 将导致以下假： 真实前向速度是真实的。

丑陋是为耦合我们的横向和纵向动态模型， 这简化了我们的建模任务， 但在加速或出现为缓慢时，确实会导致塑造不完美。

即将，同运动自行车一样， 前后轴的左右游 分别集中在一个火花上。 因此，这个假将四轮子转换成两个轮子的自行车模型。

最后的其他影响，例如举运动， 道路倾向和空气动力，可以不计较。

这些影响产生的轮胎力产生重大影响。 因此，这也是 在某些情况下的极限， 对我们的目的来说，已经是上海了。

我们将使用车辆重心作为动态模型的参考点， 因为它简化了牛顿第二法则的应用。

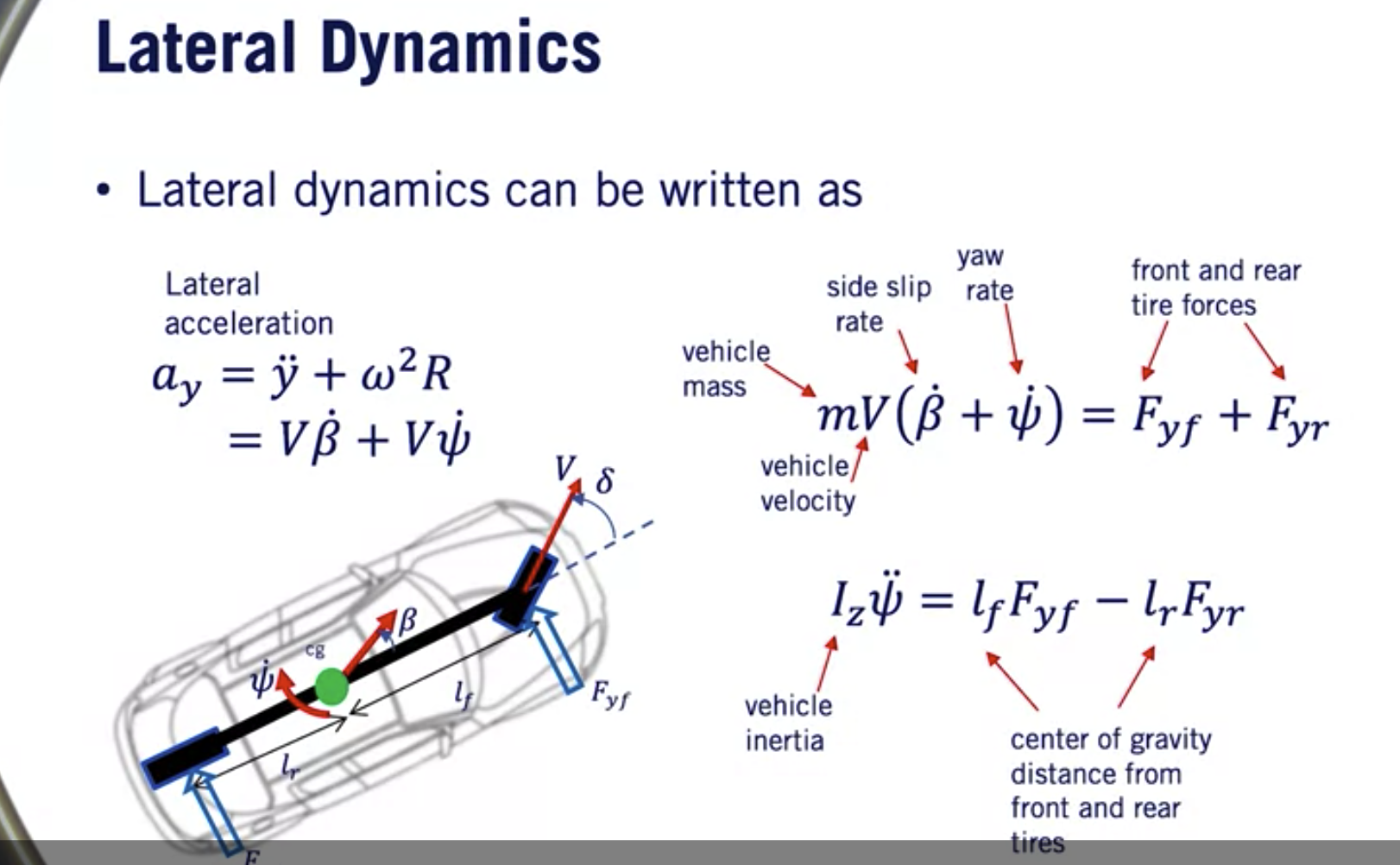
我们可以将错误系统中的总定义定义为是， 这包括在身体框架上侧向传播y的二次导， 以及车辆旋转的向心圣诞 ω的平方乘以R。

这些表达式可以 用滑移角变化率β点 和变化率， ψ点通滑移角的定义，以及V=ω*R， ω=ψ点，分别地。

横向动力学模型的公式现在可以看到与两个 力（是前轮胎和后轮胎上的侧向力）影响。

车辆动态速度由V定义， 质量为m。 由车轮力产生的力矩在 反上作用并与相向结合， iz乘以ψ的二次导得到二阶。

参数lf和lr定义了从重心到每个轮胎的距离。

车辆建模或文章中最重要的一个。

轮胎力通常准确预测， 轮胎模型往往是起源的，并由此可以看出主要由经验进行了识别。

我们将探索一些 更常见的轮胎模型，在本单元的最后的视频中。

幸运的是，在正常驾驶条件下， 一个简单的线性近似可以模拟机械力的产生。

该实际上仅对小滑移角有效， 并且车轮力被塑造为具体地随滑移角线性变化。

当我们在控制设计中使用线性轮胎模型时， 我们必须确保不超过 小角度的真实驾驶操作，非随身携带的。

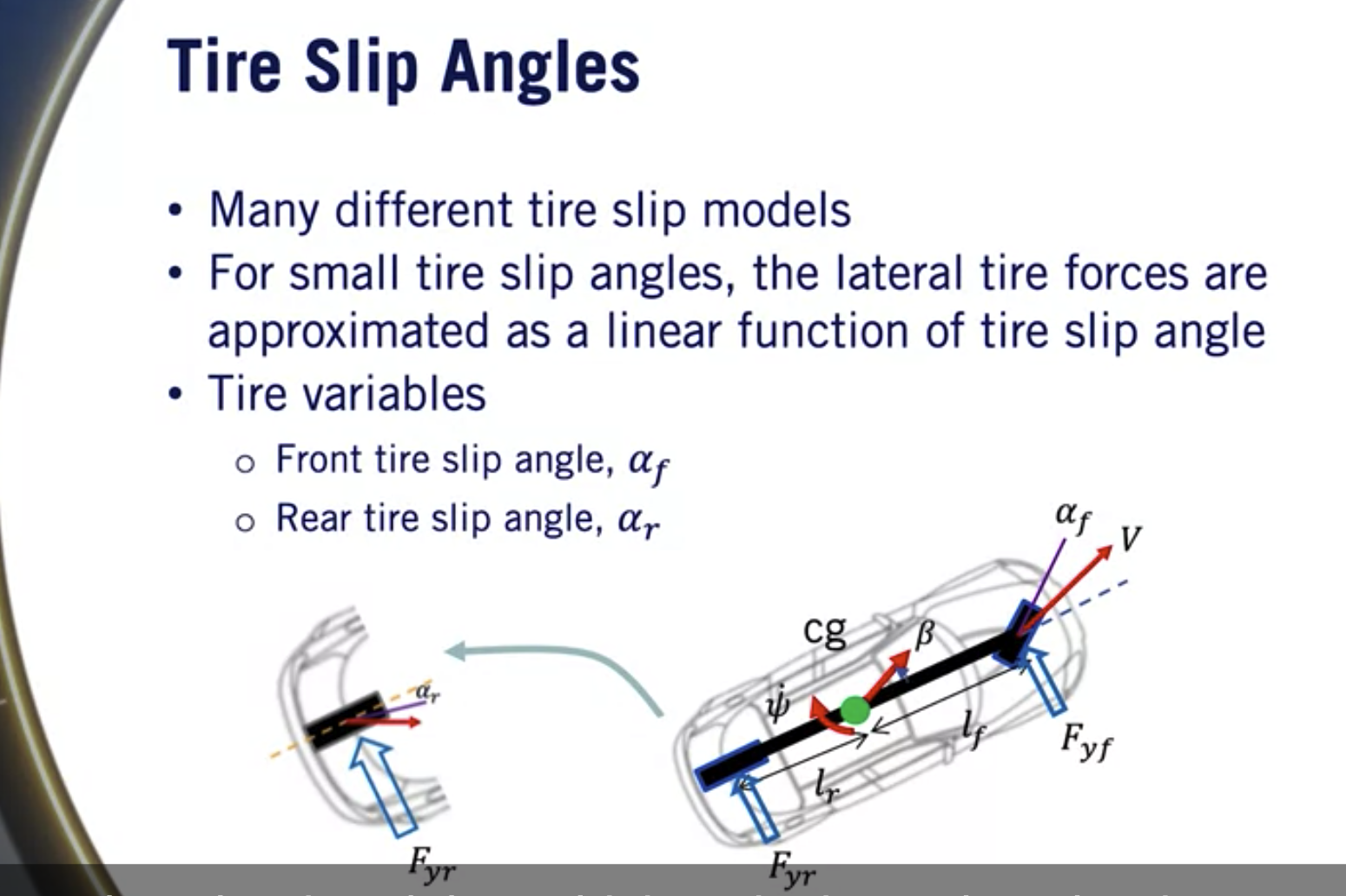
为使用这些轮胎模型， 我们需要定义前后滑移角 αf 和αr。 与车辆滑移角β完全相同的方式， 但是是相对于地球的方向 和生活中心的速度来定义。 轮的原因由 其在车辆行驶时变形的能力定义。

该图显示了 横向轮胎力与轮胎滑移角的关系。 直线在的斜率同一坐标零。

一起滑移角的下方， 通常小于8度， 我们的关系几乎是线性关系。

我们可以将 Cf 和 Cr 视为理想化 为自行车的前轮和后轮的性能。

因此，作用在 前轮和轮上的横向力的关系将是每个周期之间的关系 Cy,和滑移角 α的乘积。

我们可以逐个滑移角，根据车辆滑移β， 转向角δ， 速度纵向V， 和横摆率。

导出的横向模型的突然动态现在 可以通过替换轮胎力可能修改。

这将导致以下对战 一个常微分， 其控制车辆在横向的动态。

请注意，左侧变量表示 车辆滑移角的变化率和横摆率的变化率。

可能地并且因为 在整个推导过程中的近似和真实， 得到的动态横向车辆模型是线性的。

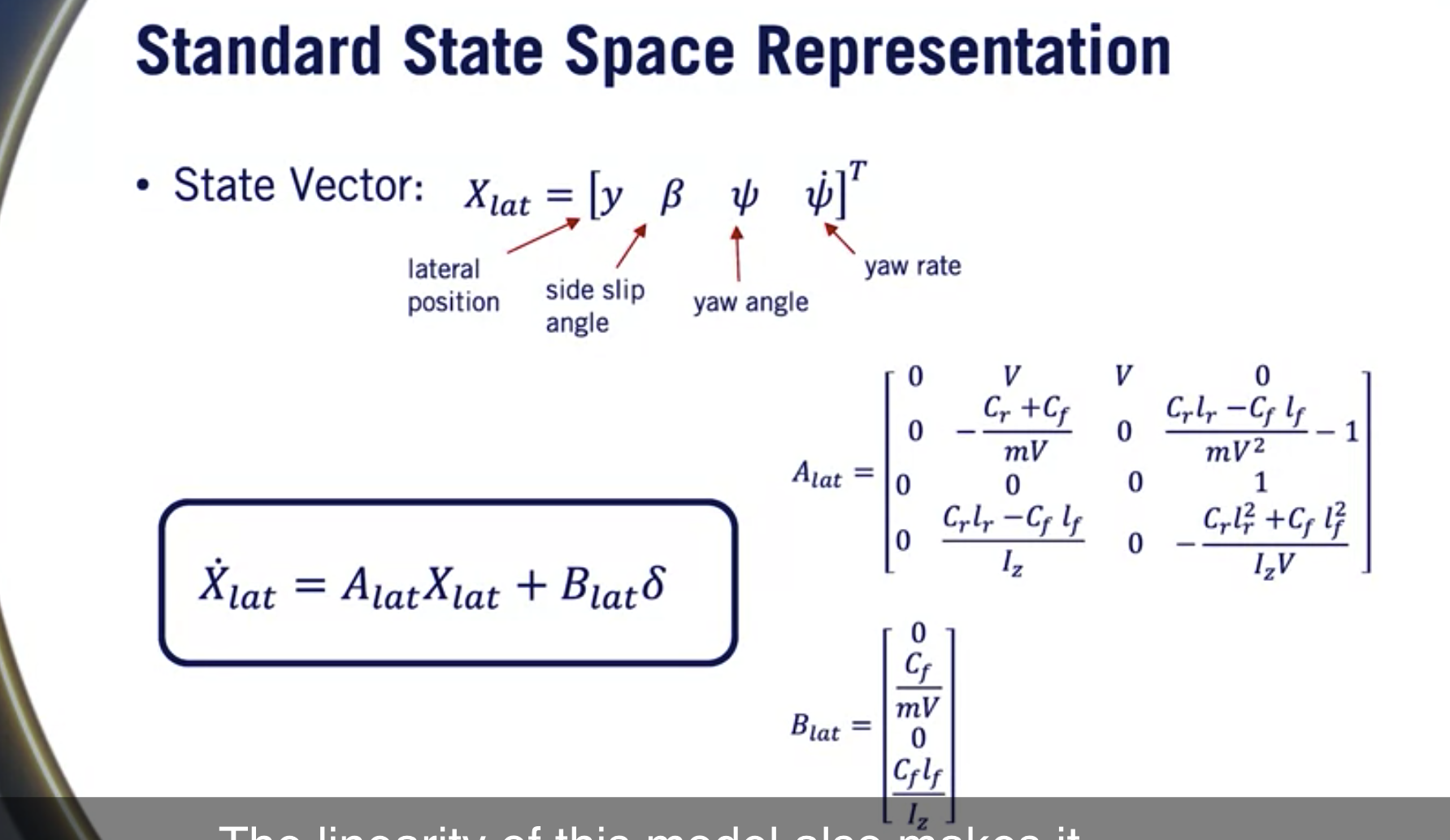
我们可以定义一个状态 X_lat，包括横向位置y， 滑移角β 偏航角ψ， 和偏航率ψ的一次导。

现在可以用标准状态空间形式表示系统，如下图 X_lat的一次导等于Alat乘以 X_lat加上B_lat乘以δ。

系统动力学矩阵为 A _ lat 和 B _ lat, 如果前进V保持不变，则它们是时不变的。

系统的主要输入是转向角度方向δ。

我们状态空间表示非常特殊的，当我们设计 不同的控制策略（例如用于横向控制的PID或MPC）时。

该模型的线性度也可以 针对于卡尔曼的状态估计， 您会在第二课程中了解更多信息。

让我们总结一下这个视频。 我们首先学会了如何扩展 我们的运动自行车模型成为一个动态的自行车模型， 然后我们得出了自行车模型的横向动力学 并以状态空间形式表达。 在下一个视频中， 我们将探索并构建车辆驱动系统的模型，包括油门， 中断和转向。下节课见。

第5课补充阅读：自行车模型的横向动力学

补充阅读：自行车模型的横向动力学
在下面的 PDF 中阅读有关自行车模型横向动力学的更多信息（第 27-44 页）：

R. Rajamani (2012)，“横向车辆动力学”在：车辆动力学和控制，机械工程系列，
https 😕/www.springer.com/cda/content/document/cda_downloaddocument/9781461414322-c1.pdf?SGWID =0 -0-45-1265143-p174267791。

• 横向车辆动力学.pdf

参考

https://www.coursera.org/learn/intro-self-driving-cars/lecture/1Opvo/lesson-5-lateral-dynamics-of-bicycle-model

今天的文章自动驾驶 4-5 自行车模型的横向动力学 Lateral Dynamics of Bicycle Model分享到此就结束了，感谢您的阅读。