这算是我编写的第一个带点智能的程序了,虽然学编程这么久了。。。。。。
本篇文章就是记录一个三连子游戏的理论、设计、实现的全部过程和思路,(五子棋 四连子 井字棋都差不多,三连子更简单一点,方便理解)
理论
我是最开始是通过人工智能 一种现代的方法第三版 这本书接触到这方面的知识的,然而书上讲解的不甚详细,还参考了网络上其他讲解这部分理论的文章
其他写的比较好的文章汇总:五子棋入门级AI的设计与实现
博弈游戏的AI设计(一):极大极小树
五子棋AI算法第四篇-启发式搜索函数
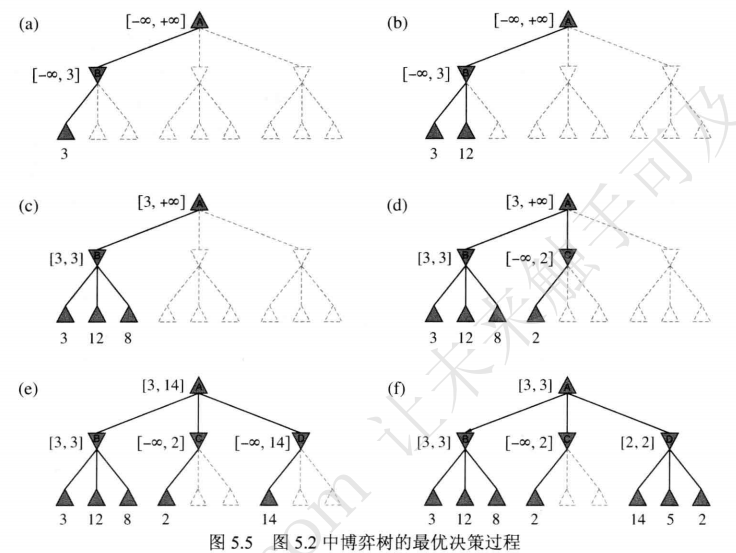
我总结下来就是极大极小值算法通过深搜来搜索双方的落子的情况,来得出最佳的落子位置,然后使用α-β剪枝加快速度,但是就算是使用α-β剪枝 剪枝了,时间上还是不可以接受
所以我们想到这样一种方法,我们不一定非要深搜到谁赢谁输才算到头(这样太慢了),我们确定一种对棋局分析的策略(评估函数),这个评估函数可以在没有确定谁输谁赢的时候给我们一个当前棋局的评估分数(更加符合人类的思考方式),我们根据评估分数作为落子的参考。
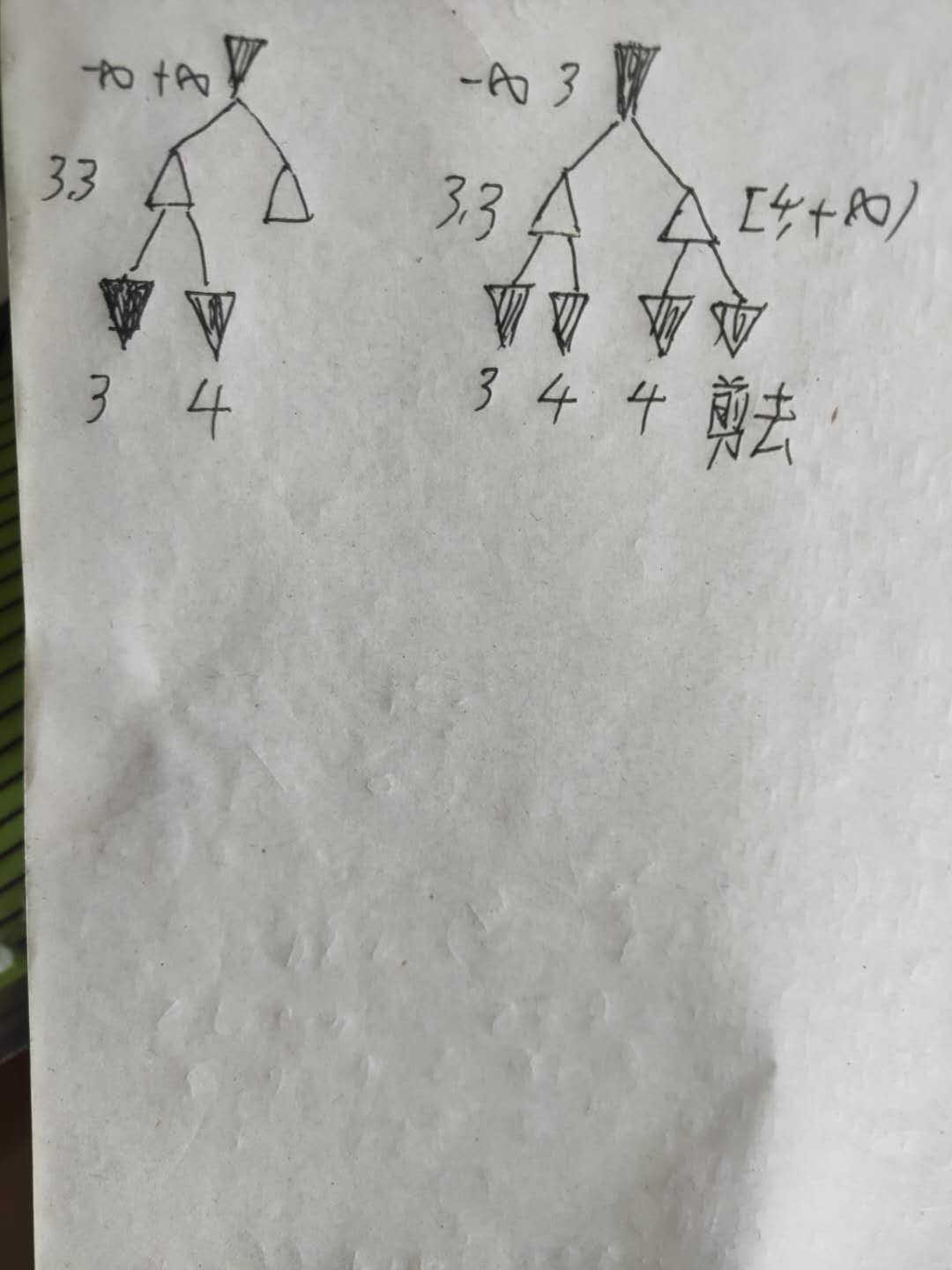
关于MAX和MIN的剪支不理解的话,可以参考下面的两个图
下面是MAX层的剪支
下面是MIN层的剪支,可以看到因为第一层MIN确定了比3小了,第二层的第二个MAX只要确定了比4大,则剩下的全部会被剪支
三连子游戏的设计
评估函数的策略应该如何设计
首先我们统计棋盘的情况,应该对两类棋子分开统计,计算机的棋子类别设为1,人类下的棋子设为2,记当前棋局1类棋子的得分为maxscore,2类棋子的得分为minscore,函数返回maxscore-minscore。 这样1类棋子得分越高,2类棋子得分越低,1类棋子赢的概率越大,也就是计算机赢的概率越大
如何计算某一类棋子的得分
本次策略是首先把棋盘上所有可以获胜的情况(3个子相连了,横竖斜均可)列举出来,比如棋盘上(0,0) (0,1) (0,2) 是三个相连的点 ,然后对这三个相连的点进行统计,看这三个点上 有人类下的棋子几个,电脑下的棋子几个,空了几个。
- 如果有人类棋子3个了,很明确已经胜利了,权重最大,记为3000
- 如果有2个人类棋子并且另一个是空的,那么人类很可能胜利,权重小一点,记为100
- 如果有2个人类棋子,1个电脑的棋子,那么人类的局势还行,权重更小,记为10
- 如果有1个人类棋子,2个空闲位置,那么人类很可能胜利,权重要再小一点,记为50
- 如果有1个人类棋子,1个电脑的棋子,那么人类的局势还行,权重更小,记为10
然后把对人类下的棋子的权重进行相加,记为maxscore
电脑的棋子也是同样的情况,所有权重相加记为minscore
python实现代码
注释量快赶上代码量了,希望都能看懂吧
import numpy as np
from tkinter import *
#导入 Tkinter 库 ,python的标准GUI
class Game(object):
def __init__(self):
#table_num 记录每个列当前能哪一行能放旗子,最初能放旗子的位置是(3,0)(3,1)(3,2)(3,3)
#三连子的规则是下棋的时候都是从每列自底向上开始的
self.table_num = [3, 3, 3, 3]
#win_sn保存着4*4棋盘的所有赢法
self.win_sn=self.getSn()
#生成棋盘
self.chess = np.zeros((4, 4), dtype=int) # 棋盘状态数组 0---空格 1---叉电脑 2---圈玩家
#iscircle 表示本次落子是不是落的圆圈,即玩家
#当iscircle为False时候,落子的是× 即电脑
self.iscircle = True # 当前圈下-,默认玩家先手
## 实例化Tk类(窗口对象)。Tk类是顶层的控件类,完成窗口的一系列初始化
self.root = Tk()
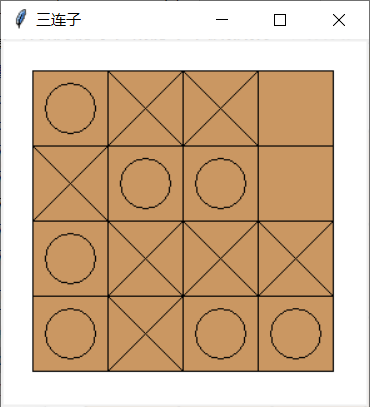
self.root.title('三连子')
#调用Tkinter 库 画布控件,生成一个白色背景的 长宽指定的画布
self.canvas = Canvas(self.root, width=290, height=290, bg="white")
#使用pack布局,从上到下,从左到右的摆放控件
self.canvas.pack()
#在画布上创建一个矩形,使用CA9762颜色填充
#另外Tkinter中的坐标系也是从左上角开始的
self.canvas.create_rectangle(25, 25, 265, 265, fill="#CA9762")
for i in range(1, 6):
self.canvas.create_line(25, 25 + 60 * (i - 1), 265, 25 + 60 * (i - 1)) # 横线
self.canvas.create_line(25 + 60 * (i - 1), 25, 25 + 60 * (i - 1), 265) # 竖线
#<Button-1>表示鼠标左键单击 绑定到player 函数,表示玩家点击了棋盘某一点后触发函数
self.canvas.bind("<Button-1>", self.player)
#主窗口循环
self.root.mainloop()
#生成4*4棋盘所有的赢法
def getSn(self):
out = []
for i in range(4):
temp_list = [(i, 0), (i, 1), (i, 2)]
out.append(temp_list)
temp_list = [(i, 1), (i, 2), (i, 3)]
out.append(temp_list)
temp_list = [(0, i), (1, i), (2, i)]
out.append(temp_list)
temp_list = [(1, i), (2, i), (3, i)]
out.append(temp_list)
# 主对角线
# 左上到右下
temp_list = [(0, 0), (1, 1), (2, 2)]
out.append(temp_list)
temp_list = [(1, 1), (2, 2), (3, 3)]
out.append(temp_list)
# 右上到左下
temp_list = [(0, 3), (1, 2), (2, 1)]
out.append(temp_list)
temp_list = [(1, 2), (2, 1), (3, 0)]
out.append(temp_list)
# 上侧的副对角线
temp_list = [(0, 1), (1, 2), (2, 3)]
out.append(temp_list)
temp_list = [(0, 2), (1, 1), (2, 0)]
out.append(temp_list)
# 下面对角线
temp_list = [(1, 0), (2, 1), (3, 2)]
out.append(temp_list)
temp_list = [(1, 3), (2, 2), (3, 1)]
out.append(temp_list)
return out
#判断是不是赢了,chesstemp 是棋盘数据,who保存1 还是2 表示棋盘中1赢了还是棋盘的2赢了
def win(self, chesstemp, who):
t = chesstemp.copy()
for list in self.win_sn:
if t[list[0][0]][list[0][1]] == who and t[list[1][0]][list[1][1]] == who and t[list[2][0]][list[2][1]] == who:
return True
return False
def isGameOver(self, who):
# 游戏结束 的三个情况 1、满格平局 2、电脑胜,棋子1赢了 3、玩家胜 棋子2赢了
t = self.chess.copy()
#判断是不是赢了
if self.win(t, who):
return True
else:
#判断棋盘还有哪些位置空闲
empty_cells = [(i, j) for i in range(4) for j in range(4) if t[i][j] == 0]
if len(empty_cells) == 0: # 没有人赢,但是没有空格了,游戏结束
return True
else: # 游戏没有结束
return False
#画圈,i j表示在4*4 棋盘的那个位置画,函数内部完成坐标转换
def drawcircle(self, i, j):
x = 25 + 60 * j
y = 25 + 60 * i
self.canvas.create_oval(x + 30 - 20, y + 30 - 20, x + 30 + 20, y + 30 + 20)
#画×,i j表示在4*4 棋盘的那个位置画,函数内部完成坐标转换
def drawcha(self, i, j):
x = 25 + 60 * j
y = 25 + 60 * i
self.canvas.create_line(x, y, x + 60, y + 60)
self.canvas.create_line(x + 60, y, x, y + 60)
# 通过按钮事件来调用play,表示玩家下棋,玩家下完后需要电脑落子了
# 所以play函数里面还会再调用电脑的下棋函数 self.computer()
def player(self, event):
y = event.y
x = event.x
if self.iscircle and (25 <= x <= 265) and (25 <= y <= 265):
#确定鼠标左键单击时的坐标对应棋盘几行 几列
i = int((y - 25) / 60)
j = int((x - 25) / 60)
#由于三连子的规则,我们确定了列其实就是说在该列最低处落子
#所以对于鼠标左击的坐标只用到X轴的值 即J,帮助确定那一列
#而table_num保存着每一列的哪一行当前可以落子
i = self.table_num[j]
#这样我们在棋盘上的落子就确定下来了 (i,j)
if i >= 0:
#棋盘上 落子,玩家的棋子用2来表示
self.chess[i][j] = 2
#table_num 储存着j列的的落子行下标-1
self.table_num[j] -= 1
# 画圈
self.drawcircle(i, j)
# 画完,判断是否结束游戏
get = self.isGameOver(2)
if get:
print("--------你竟然赢了-------")
else:
# 轮到电脑下
self.computer()
else:
print("--------该列已经满了,换个列吧-------")
def computer(self):
#计算机的下棋函数,计算机下1这类棋子,该函数的目的是确保棋盘中1的棋子能够胜利
# 进行 a-b剪枝 ,返回下一步该下的坐标 程序的关键之一
i, j, score = self.alphabeta(self.chess, -3000, 3000, True,6) # 树的深度限制
print('Computer下棋的位置 ,i ,j ', i, j, score)
#画×
self.drawcha(i, j)
#棋盘落子
self.chess[i][j] = 1
#table_num 储存着j列的落子行下标需要减去1
self.table_num[j] -= 1
isGameOver = self.isGameOver(1)
if isGameOver:
print("--------你果然输了-------")
else:
self.iscircle = True
#对于alpha beta 剪支算法,我的理解是对极小极大算法的优化
# 在MAX层主要更新alpha ,在MIN层主要更新Beta
#然后不论是MAX层还是MIN层,除了自己本身需要不断优化alpha或者beta (初始值负无穷和正无穷)
#我这里的程序是把-2000 2000看成正负无穷
# 还需要保留上一层的 alpha beta用于剪支
def alphabeta(self, chessborad, alpha, beta, isMax, depth):
#复制棋局
tempChess = chessborad.copy()
if isMax: # MAX 计算机 下1这种棋子
#parent记录从上一级过来的alpha beta 值,用于剪支
alpha_parent = alpha
beta_parent = beta
alpha=-3000
beta=3000
#棋盘哪些位置可以落子,因为三连子的规则,每一步都只能在当前列的最后一个
empty_cells=[]
for j in range(4):
if(self.table_num[j]>=0):
i=self.table_num[j]
empty_cells.append((i,j))
#如果还是有空位的话
if len(empty_cells) != 0:
#最后输出本次max层最有利 的下棋位置,先默认是第一个下棋点
#change_i 保存着当前MAX层 能确保score最大的放置棋子的地方
change_i, change_j = empty_cells[0]
for index in range(len(empty_cells)):
#获取本次循环确定的落子地点
i, j = empty_cells[index]
#落子
tempChess[i][j] = 1
#落子的j列对应的行标需要减去1
self.table_num[j] -= 1
#评估落子后的局势
score = self.evaluate(tempChess)
#当还有深度或者当前没有赢,因为大于2000就认为棋子1已经胜利了
if depth>0 and score<2000:
# 深搜,注意这里传递是alpha beta
# 因为alpha可能会在完成一次深搜之后更新
#可以看看人工智能:一种现代的方法(第3版)图片5-5的示例
temp_i, temp_j, score = self.alphabeta(tempChess, alpha, beta, not isMax, depth - 1)
#之前落子的列,把位置再空值出来
self.table_num[j] += 1
tempChess[i][j] = 0
#当递归获得或者是直接计算当前局势的评分比alpha大,就更新alpha
if score > alpha:
alpha = score
change_i, change_j = i, j
print("MAX更新alpha为:", alpha)
print("在",depth,'轮MAX下棋位置为 (', i,",", j,")时候的评分:", score)
# 输出当前的棋盘情况
print(tempChess)
if alpha > beta_parent:
print('剪枝了')
break
print("在",depth, '轮MAX下棋最终位置和评分为',change_i, change_j,' score为', alpha)
return change_i, change_j, alpha
else:
# 深度不为0,但是没有空位了,不再继续向下搜索,将当前节点当做子节点进行评价
score = self.evaluate(tempChess)
if score > alpha:
alpha = score
print("在",depth, '轮MAX,无空位时评分为 score为', alpha)
return -1, -1, alpha
else: # MIN
# MIN结点剪支需要的MAX父节点的 beta值
alpha_parent = alpha
beta_parent = beta
empty_cells = []
for j in range(4):
if (self.table_num[j] >= 0):
i = self.table_num[j]
empty_cells.append((i, j))
if len(empty_cells) != 0: # 有MIN节点
change_i, change_j = empty_cells[0]
for index in range(len(empty_cells)):
i, j = empty_cells[index]
tempChess[i][j] = 2
self.table_num[j] -= 1
score = self.evaluate(tempChess)
if depth > 0 and score > -2000:
# 进一步递归下一层的MAX
temp_i, temp_j, score = self.alphabeta(tempChess, alpha, beta, not isMax, depth - 1)
self.table_num[j] += 1
tempChess[i][j] = 0
if score < beta:
beta = score
change_i, change_j = i, j
print("在",depth,'轮MIN下棋位置为 (', i,",", j,")时候的评分:", score)
print(tempChess)
if beta < alpha_parent:
print('剪枝了')
break
print("在",depth, '轮MIN下棋最终位置和评分为',change_i, change_j,' score为', beta)
return change_i, change_j, beta
else:
# 深度不为0,但是没有子节点,不再继续向下搜索,将当前节点当做子节点进行评价
score = self.evaluate(tempChess)
if score < beta:
beta = score
print("在",depth, '轮MIN,无空位时评分为 score为', beta)
return -1, -1, beta
# 评估函数,计算机有点聪明劲头儿的精髓
#首先这个评估函数就是分析出,当前的棋盘的局势对双方的胜率有多大
#因为我们这里是编写一个尽量智能的计算机下棋程序,所欲评估函数对于
#计算机的棋子1 胜利的情况要尽可能返回最大值,对于人下的棋子2胜利的情况要尽可能
#返回最小值,为了满足这样的要求,我们对 棋子1评估取胜分数为maxscore,
# 对棋子2评估取胜分数minscore,然后让函数返回maxscore-minscore
def evaluate(self, chessborad):
#默认 棋子1取胜的分数maxscore是0, 棋子2取胜的分数minscore是0
maxscore = 0
minscore=0
# win_sn 保存着所有可能的取胜路径,对所有路径进行遍历
for list in self.win_sn:
#保存取胜路径上棋子的数目,比如signNum[0] 就是在取胜路径上0棋子的个数
signNum=[0,0,0]
#这个sign主要是对取胜路径进行判断,比如我们当前棋盘是这样婶儿的
# 2 2 0 0
# 1 1 0 0
# 2 2 0 0
# 1 1 0 0
#这个时候大概率取胜应该是1,因为根据三连子的规则,下一个棋子只能放在(3,2)这个位置
sign = 1
for tuple in list:
#tuple[0] 是当前遍历的取胜路径的行下标
#还是上面那个例子,如果遍历到的取胜路径是 (0,0) (0,1) (0,2)
# 而棋盘上0 1 2 列对应可以放置棋子的行数是 -1 -1 3
#所以取胜路径上行下标小于 可以防止棋子的行下标的时候,本次取胜路径就不可取
if tuple[0] <self.table_num[tuple[1]]:
sign=-1
break
#统计取胜路径上 0 1 2棋子的个数
signNum[chessborad[tuple[0]][tuple[1]]]+=1
if sign==1:
#已经取胜了,取胜设置权重为3000
if signNum[1] == 3:
maxscore += 3000
# 2缺1
#2个1棋子,另一个是空白位置,有很大可能赢,所以设置权重为100
elif signNum[1] == 2 and signNum[0] == 1 :
maxscore += 100 * signNum[1]
# 2个1棋子,1个2棋子,赢得可能再小一点
elif signNum[1] == 2 and signNum[2] == 1:
maxscore += 10 * signNum[1]
# 3缺2
#只有一个1棋子,其他两个位置是空白的
if signNum[1] == 1 and signNum[0] == 2:
maxscore += 50 * signNum[1]
#1个1棋子 2个2棋子
elif signNum[1] == 1 and signNum[2] == 2:
maxscore += 10 * signNum[1]
# min的
# 二缺1
if signNum[2] == 3:
minscore += 3000
if signNum[2] == 2 and signNum[0] == 1 :
minscore += 100 * signNum[2]
elif signNum[2] == 2 and signNum[1] == 1:
minscore += 10 * signNum[2]
# 3缺2
elif signNum[2] == 1 and signNum[0] == 2:
minscore += 50 * signNum[2]
elif signNum[2] == 1 and signNum[1] == 2:
minscore += 10 * signNum[2]
return maxscore - minscore
if __name__ == '__main__':
Game()
今天的文章人工智能-三连子游戏设计和实现分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/62716.html