卷积，反卷积，空洞卷积

卷积神经网络中卷积核的作用在于特征的抽取，越是大的卷积核尺寸就意味着更大的感受野，当然随之而来的是更多的参数。早在1998年，LeCun大神发布的LetNet-5模型中就会出，图像空域内具有局部相关性，卷积的过程是对局部相关性的一种抽取。

但在深度卷积网络中，我们使用多次池化，下采样在增大感受野的同时使得信号的分辨率变小。且在卷积池化的过程中，尺寸会快速变小，我们常常会使用填充手段来解决这个问题。但填充通过会引起一些噪声，损失了大量的信息。但由于图像分割预测是pixel-wise的输出，所以将pooling后较小的图像上采样（upsampling）到原始的图像尺寸进行预测一般需要采用反卷积（deconv）操作。之前pooling一般为max pooling，所以该pooling操作使得每个pixel能预测都能看大较大感受野信息。我们如何在增大感受野的同时解决池化带来的弊端呢？空洞卷积应运而生！但同样有填充的操作，到底空洞卷积与反卷积，填充操作有什么区别呢？首先先了解各个操作！

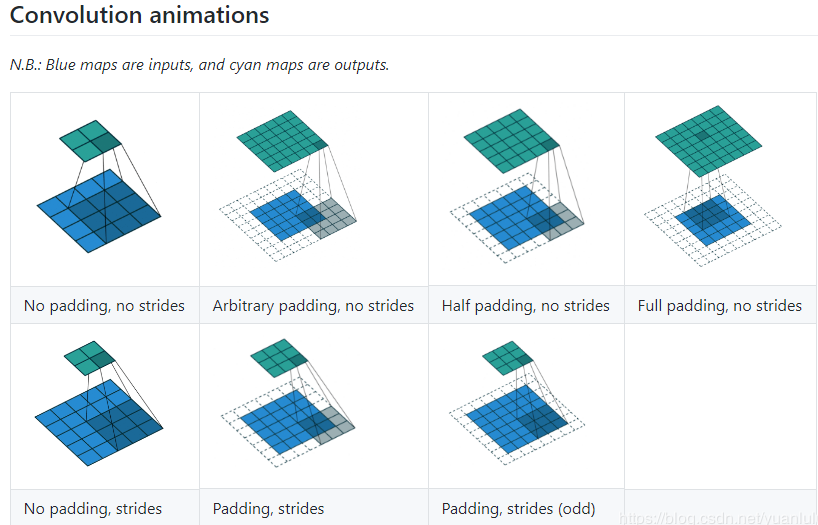
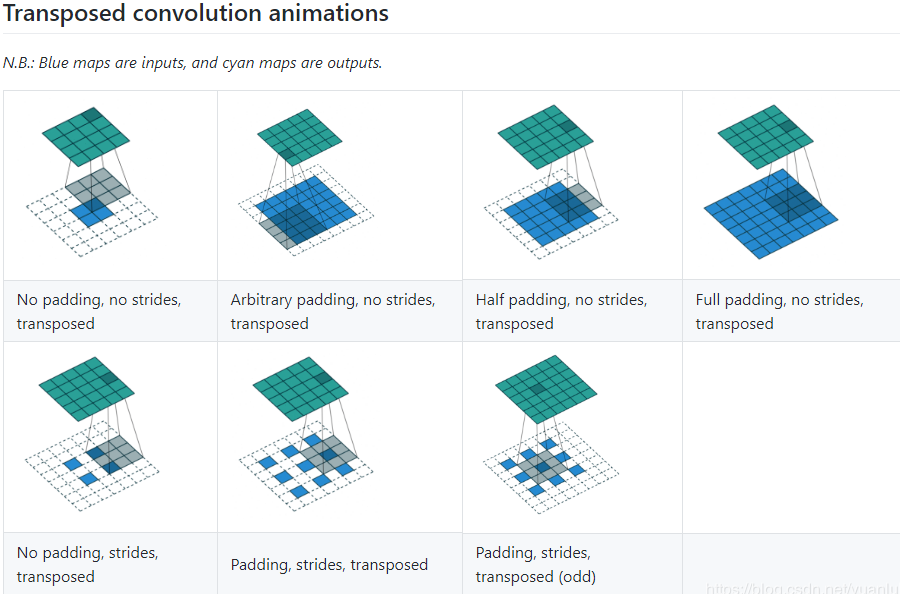
在介绍之前先视觉上了解卷积，反卷积，空洞卷积是如何工作的。 

反卷积（deconv）：

主要用于增大图像尺寸，是upsampling的一种，而空洞卷积并没有做upsampling，空洞卷积是为了增大感受野，可以不改变图像的大小。
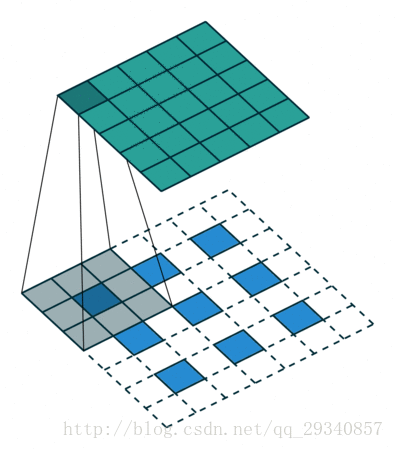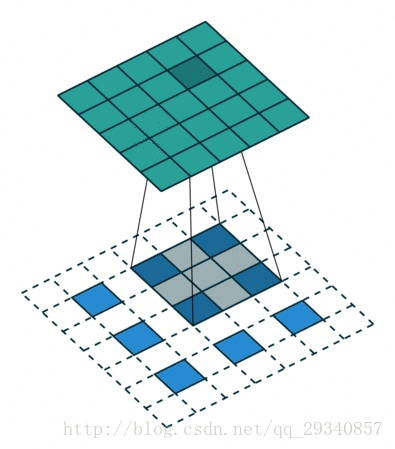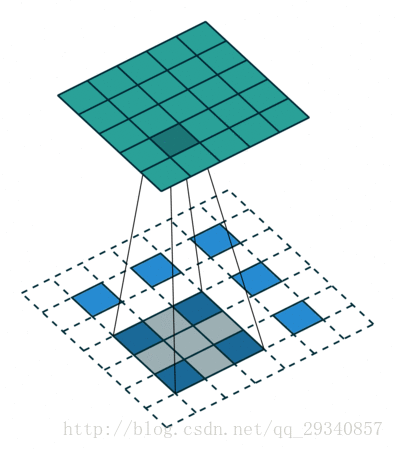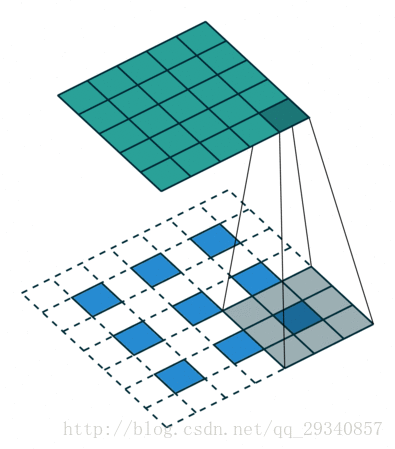
对于反卷积简单理解就是在输入特征矩阵中插入空白点，再进行卷积，这样卷积后输出的特征矩阵就变大了。

对于标准k*k卷积核，stride为s，分三种情况：

1） s>1 ,在卷积同时伴随着downsampling操作，卷积后图像变小了（这种操作也可以增大感受野，但是输出的图像大小变小了）
2） s=1 ,在padding设置为stride大小时，卷积后图片大小不变
3）s<1,相当于对原图作upsampling操作进行扩大原图，然后再卷积，这样得到的结果图就变大了。例如s=0.5意味着在原特征图的每相邻数据间插入一个空白数据，这样再进行卷积，它的输出特征图就变大了。

上面3）所描述的就是反卷积，它的核心是在原来图像上插入空白数据。而空洞卷积就是在卷积核插入空白数据，或是说在卷积时跳过特征图的部分数据。

反卷积的类型

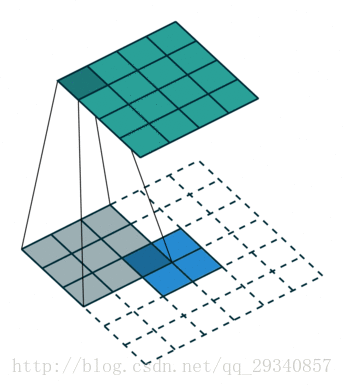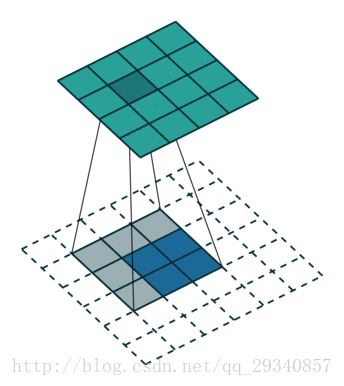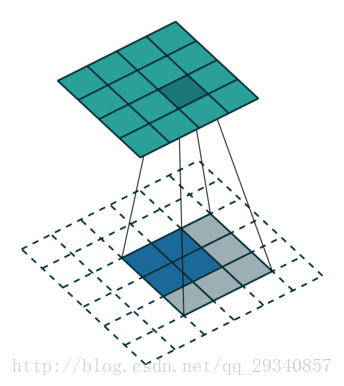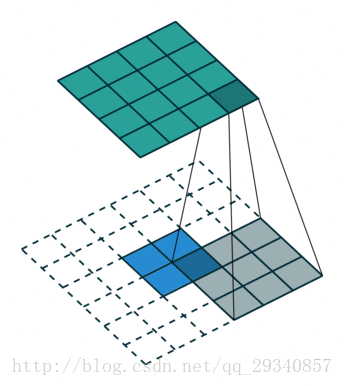
1.一般类型： 

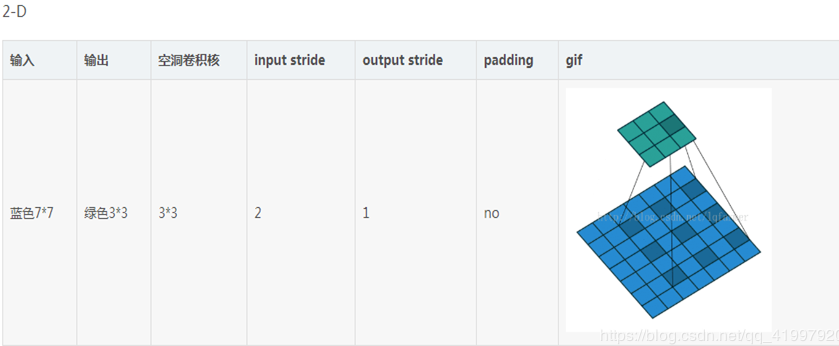
• 输入：2*2 
• 计算过程：2+2*2-3+1 
• 输出：4

• 输入：3*3 
• 计算过程：3+4-3+1 
• 输出：5

详细解释：反卷积原理
 

空洞卷积

首先是诞生背景，在图像分割领域，图像输入到CNN（典型的网络比如FCN）中，FCN先像传统的CNN那样对图像做卷积再pooling，降低图像尺寸的同时增大感受野，但是由于图像分割预测是pixel-wise的输出，所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测（upsampling一般采用deconv反卷积操作，之前的pooling操作使得每个pixel预测都能看到较大感受野信息。因此图像分割FCN中有两个关键，一个是pooling减小图像尺寸增大感受野，另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中，肯定有一些信息损失掉了，空洞卷积使得通过pooling也能有较大的感受野看到更多的信息。

dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者语音文本需要较长的sequence信息依赖的问题中，都能很好的应用dilated conv，比如图像分割、语音合成WaveNet、机器翻译ByteNet[1]中。简单贴下ByteNet和WaveNet用到的dilated conv结构，可以更形象的了解dilated conv本身。

(a)图对应3×3的1-dilated conv，和普通的卷积操作一样，(b)图对应3×3的2-dilated conv，实际的卷积kernel size还是3×3，但是空洞为1，也就是对于一个7×7的图像patch，只有9个红色的点和3×3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为7×7，但是只有图中的9个点的权重不为0，其余都为0。 可以看到虽然kernel size只有3×3，但是这个卷积的感受野已经增大到了7×7（如果考虑到这个2-dilated conv的前一层是一个1-dilated conv的话，那么每个红点就是1-dilated的卷积输出，所以感受野为3×3，所以1-dilated和2-dilated合起来就能达到7×7的conv）,(c)图是4-dilated conv操作，同理跟在两个1-dilated和2-dilated conv的后面，能达到15×15的感受野。对比传统的conv操作，3层3×3的卷积加起来，stride为1的话，只能达到(kernel-1)*layer+1=7的感受野，也就是和层数layer成线性关系，而dilated conv的感受野是指数级的增长。

要理解空洞概念和如何操作可以从两个角度去看
1）从原图角度，所谓空洞就是在原图上做采样。采样的频率是根据rate参数来设置的，当rate为1时候，就是原图不丢失任何信息采样，此时卷积操作就是标准的卷积操作，当rate>1，比如2的时候，就是在原图上每隔一（rate-1）个像素采样，如图b，可以把红色的点想象成在原图上的采样点，然后将采样后的图像与kernel做卷积，这样做其实变相增大了感受野
2）从kernel角度去看空洞的话就是扩大kernel的尺寸，在kernel中，相邻点之间插入rate-1个零，然后将扩大的kernel和原图做卷积 ，这样还是增大了感受野。

在VGG网络中就证明了使用小卷积核叠加来取代大卷积核可以起到减少参数同时达到大卷积核同样大小感受野的功效。但是通过叠加小卷积核来扩大感受野只能线性增长，而空洞卷积可以以指数级增长感受野。
 

今天的文章卷积，反卷积，空洞卷积分享到此就结束了，感谢您的阅读。