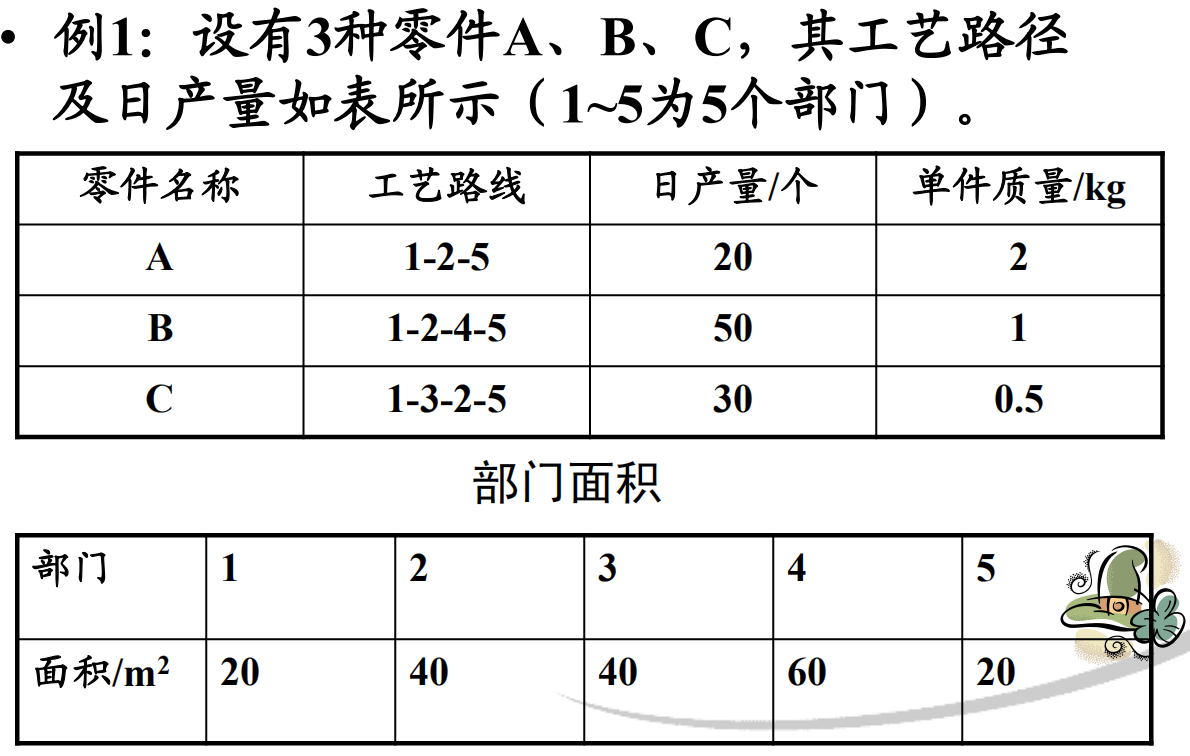
定量布置程序(CRAFT,Computerized Relationship Facilities Technique),和基于密切程度等级的ALDEP和CORELAP相反,CRAFT使用物流信息或从制表上累加而得出的作业单位物流强度。为此,CRAFT被称为定量布置程序,而前两个方法被称为定性布置程序。CRAFT是一种改进程序,这意味着CRAFT接受一项初始布置设计并用顺序方式成对交换作业单位的位置,试图做出改进。几个设计方案相互比较时,CRAFT用物品搬移或运输成本作为评价标准,这个成本用移动距离的线性函数来表示。一项好的设计是搬移成本较低。
定义描述来源
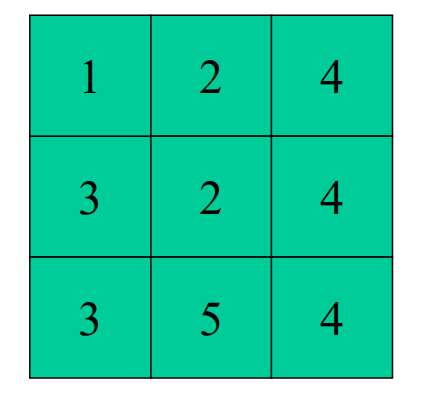
初始布局方案:
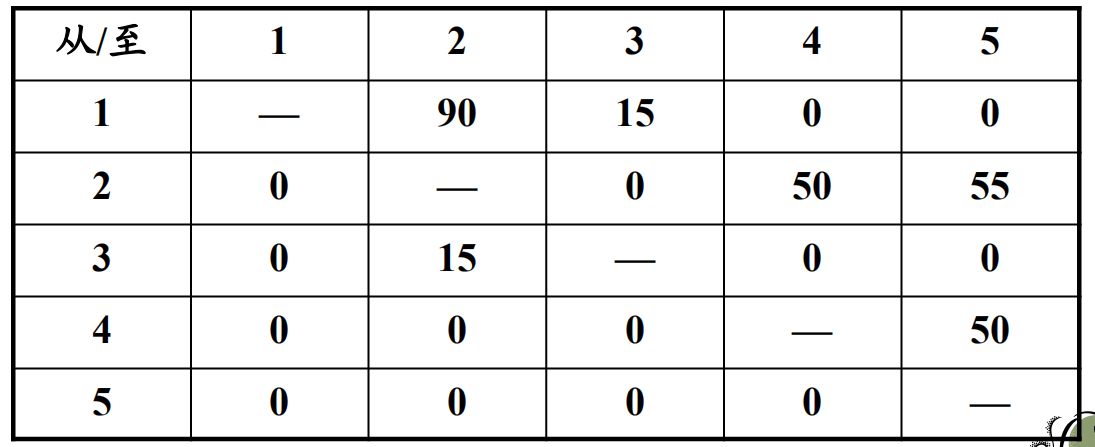
初始方案布局物流量:
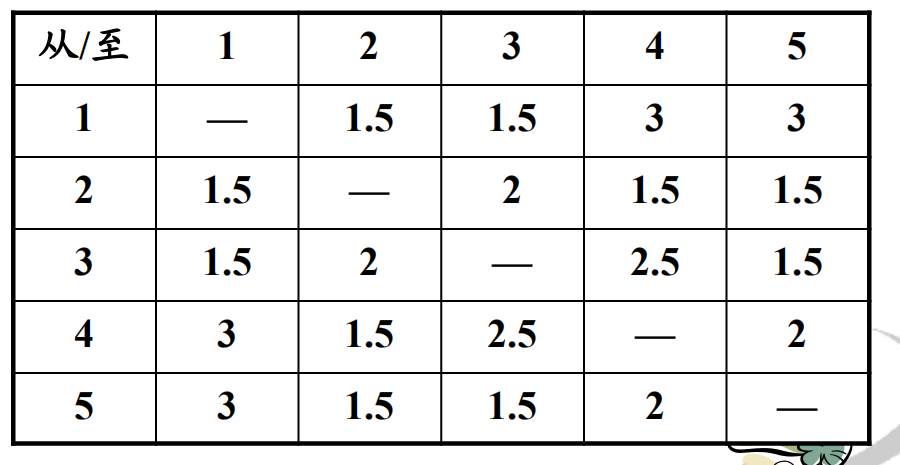
初始方案搬运距离:
方案费用=sum{物流量X距离X单位距离费用}
然后交换部门,交换原则是具有公共边或者面积相等的部门进行交换,且同一部门的若干块相连。
具体实现方法为:
//CRAFT程序方法
#include<iostream>
#include<cmath>
using namespace std;
int main() {
//初始数据定义
int material_number = 3;
int depart_number = 5;
double material_flow[5][5] = {
{
0,90,15,0,0},{
0,0,0,50,55},{
0,15,0,0,0},{
0,0,0,0,50},{
0,0,0,0,0} };//部门间物流量矩阵
double material_distance[5][5];//部门间距离矩阵
double material_cost[5][5];//部门搬运费用矩阵
double material_cost_best = 1000000;//初始最小费用值
int material_relation_best[3][3];//最优方案记录及更新
//部门关系交换
for (int i = 0; i < material_number;i++) {
for (int j = 0; j < material_number;j++) {
for (int p = 0; p < material_number;p++) {
for (int q = 0; q < material_number; q++) {
int material_relation[3][3] = {
{
1,2,4}, {
3,2,4}, {
3,5,4} };
int relation_temp = 0;
//逐一交换
relation_temp = material_relation[i][j];
material_relation[i][j] = material_relation[p][q];
material_relation[p][q] = relation_temp;
//交换结果
cout << "关系表:" << endl;
for (int m = 0; m < material_number; m++) {
for (int n = 0; n < material_number; n++) {
cout << material_relation[m][n] << " "; }cout << endl; }
//索引2,3,4当前位置
int relation_raw_temp[7] = {
0 };//行记录
int relation_column_temp[7] = {
0 };//列记录
for (int m = 0; m < material_number; m++) {
for (int n = 0; n < material_number; n++) {
if (material_relation[m][n] == 2) {
if (relation_raw_temp[0] == 0) {
relation_raw_temp[0] = m + 1; relation_column_temp[0] = n + 1; }
else {
relation_raw_temp[1] = m + 1; relation_column_temp[1] = n + 1; }
}
if (material_relation[m][n] == 3) {
if (relation_raw_temp[2] == 0) {
relation_raw_temp[2] = m + 1; relation_column_temp[2] = n + 1; }
else {
relation_raw_temp[3] = m + 1; relation_column_temp[3] = n + 1; }
}
if (material_relation[m][n] == 4) {
if (relation_raw_temp[4] == 0) {
relation_raw_temp[4] = m + 1; relation_column_temp[4] = n + 1; }
else if(relation_raw_temp[5] == 0) {
relation_raw_temp[5] = m + 1; relation_column_temp[5] = n + 1; }
else {
relation_raw_temp[6] = m + 1; relation_column_temp[6] = n + 1; }
}
}
}
/*cout << endl << "2-3当前位置:" << endl; cout << "行"; for (int m = 0; m < 7; m++) { cout << relation_raw_temp[m] << "\t"; } cout << endl << "列"; for (int m = 0; m < 7; m++) { cout << relation_column_temp[m] << "\t"; } cout << endl;*/
//3个if为2,3,4邻边条件判断
if (((relation_raw_temp[0] == relation_raw_temp[1])&&(abs(relation_column_temp[0] - relation_column_temp[1]) == 1)) || ((relation_column_temp[0] == relation_column_temp[1])&&(abs(relation_raw_temp[0]-relation_raw_temp[1])==1))) {
if (((relation_raw_temp[2] == relation_raw_temp[3]) && (abs(relation_column_temp[2] - relation_column_temp[3]) == 1)) || ((relation_column_temp[2] == relation_column_temp[3]) && (abs(relation_raw_temp[2] - relation_raw_temp[3]) == 1))) {
if (((relation_column_temp[4]== relation_column_temp[5])&& (relation_column_temp[4] == relation_column_temp[6]))||((relation_raw_temp[4]== relation_raw_temp[5])&&(abs(relation_column_temp[5]- relation_column_temp[6])==1))||((relation_column_temp[4] == relation_column_temp[6]) && (abs(relation_raw_temp[5] - relation_raw_temp[6]) == 1))) {
//计算部门间距离
double relation_raw[5] = {
0 };
double relation_column[5] = {
0 };
//索引部门当前位置
for (int m = 0; m < material_number; m++) {
for (int n = 0; n < material_number; n++) {
if (material_relation[m][n] == 1) {
relation_raw[0] += m + 1; relation_column[0] += n + 1; }
if (material_relation[m][n] == 2) {
relation_raw[1] += m + 1; relation_column[1] += n + 1; }
if (material_relation[m][n] == 3) {
relation_raw[2] += m + 1; relation_column[2] += n + 1; }
if (material_relation[m][n] == 4) {
relation_raw[3] += m + 1; relation_column[3] += n + 1; }
if (material_relation[m][n] == 5) {
relation_raw[4] += m + 1; relation_column[4] += n + 1; }
}
}
relation_raw[1] = double((int)(relation_raw[1] / 2.0 * 10)) / 10.0; relation_column[1] = double((int)(relation_column[1] / 2.0 * 10)) / 10.0;
relation_raw[2] = double((int)(relation_raw[2] / 2.0 * 10)) / 10.0; relation_column[2] = double((int)(relation_column[2] / 2.0 * 10)) / 10.0;
relation_raw[3] = double((int)(relation_raw[3] / 3.0 * 10)) / 10.0; relation_column[3] = double((int)(relation_column[3] / 3.0 * 10)) / 10.0;
/*cout << endl << "部门当前位置:" << endl; cout << "行"; for (int m = 0; m < depart_number; m++) { cout << relation_raw[m] << "\t"; } cout << endl << "列"; for (int m = 0; m < depart_number; m++) { cout << relation_column[m] << "\t"; } cout << endl;*/
//计算距离矩阵
for (int m = 0; m < depart_number; m++) {
for (int n = 0; n < depart_number; n++) {
material_distance[m][n] = fabs(relation_raw[m] - relation_raw[n]) + fabs(relation_column[m] - relation_column[n]);
}
}
cout << endl << "当前距离矩阵:" << endl;
for (int m = 0; m < depart_number; m++) {
for (int n = 0; n < depart_number; n++) {
cout << material_distance[m][n] << "\t"; }cout << endl; }
//计算部门搬运费用矩阵
double local_best = 0;
for (int m = 0; m < depart_number; m++) {
for (int n = 0; n < depart_number; n++) {
material_cost[m][n] = material_flow[m][n] * material_distance[m][n];
local_best += material_cost[m][n];
}
}
cout << endl << "当前费用矩阵:" << endl;
for (int m = 0; m < depart_number; m++) {
for (int n = 0; n < depart_number; n++) {
cout << material_cost[m][n] << "\t"; }cout << endl; }
//更新方案最优值,并记录最优关系表;
if (local_best < material_cost_best) {
material_cost_best = local_best;
for (int m = 0; m < material_number; m++) {
for (int n = 0; n < material_number; n++) {
material_relation_best[m][n] = material_relation[m][n];
}
}
}
else {
material_cost_best = material_cost_best;
for (int m = 0; m < material_number; m++) {
for (int n = 0; n < material_number; n++) {
material_relation_best[m][n] = material_relation_best[m][n];
}
}
}
cout << "局部方案:" << endl;
cout << "当前关系表费用值=" << local_best << endl;
cout << "局部搬运费用=" << material_cost_best << endl << "局部方案布局:" << endl;
for (int i = 0; i < material_number; i++) {
for (int j = 0; j < material_number; j++) {
cout << material_relation_best[i][j] << " "; }cout << endl; }
}
}
}
}
}
}
}
cout << "=================================================================" << endl;
cout << "最优方案:" << endl;
cout << "最小搬运费用=" << material_cost_best <<endl<<"最优方案布局:"<<endl;
for (int i = 0; i < material_number; i++) {
for (int j = 0; j < material_number; j++) {
cout << material_relation_best[i][j] << " ";
}
cout << endl;
}
cout << "=================================================================" << endl;
system("pause");
return 0;
}
以上方法较为笨拙,更为简便的方法还在学习当中或者麻烦各位大佬分享!
更新
在部门划分的栅格较多时,部门交换的位置约束难以使用上述方法进行控制,因此需要更为一般的交换原则进行交换。
(一)交换原则
1.1部门面积相同
以上图中部门2和部门3为例,两个部门的栅格数量相同。当两者进行交换时,可直接将部门对应的栅格进行交换。
1.2部门面积不相同
以上图中部门2和部门4为例,两个部门的栅格数量不相同。若先交换一个栅格,交换方式一共有232种,简单的方式是循环遍历。但是当部门2有m个栅格,部门4有n个栅格(m<n)时,交换方式一共有m!*n!。
若m>20或者m>50甚至更大时,循环遍历显然是不可取的。
1.3多线交叉取交换位置原则(本人随意取得_)
多线交叉取交换位置原则是一种简化循环遍历位置的一种方法。方法取固定个数的交换位置,不需遍历,所以无法获得准确的最优方案。
因此,是一种近似求解方法。
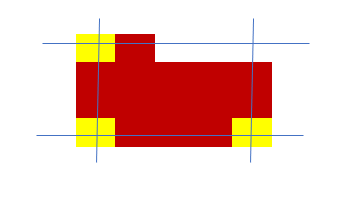
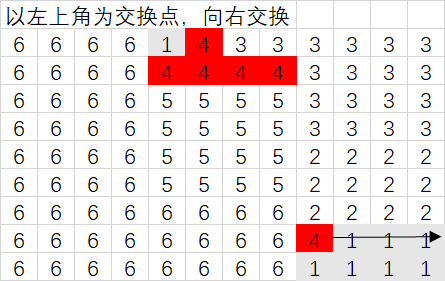
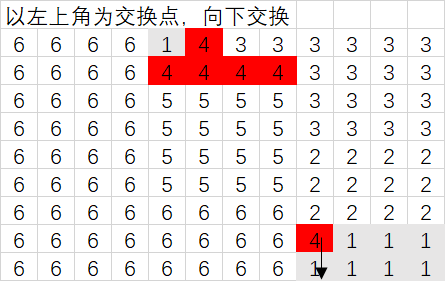
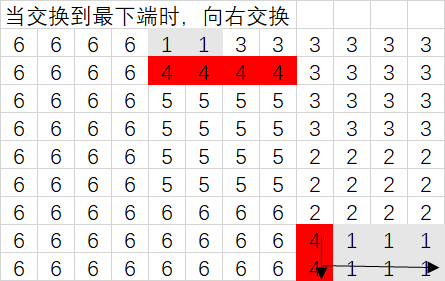
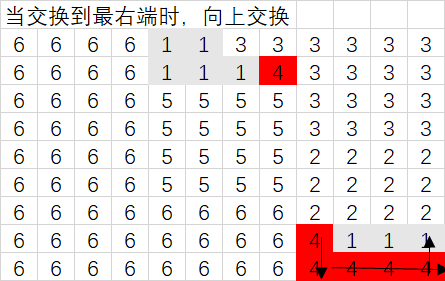
多线交叉取交换位置原则需要按照一定要求选定相应数量的不同位置的直线,不同直线之间的交点处于部门栅格处,则将该栅格作为交换栅格,同时需要选定每个交换点上的交换方向。一般交点越多,交换次数越多,越接近最优值;同时,差值也越多。
以四线交叉取点为例,如下图。红色与黄色区域之和为一个部门,蓝色线条为取点线,黄色为不同线的交点。则该部门交换的起始位置有3个,另一个点不属于该部门。
1.4 交换示例
将部门4和部门1交换
划线:
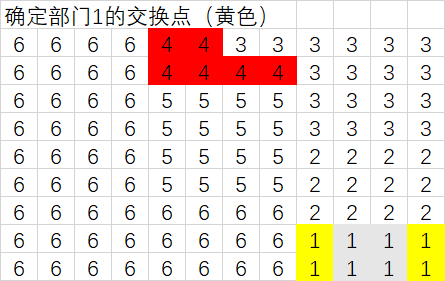
确定交换点:
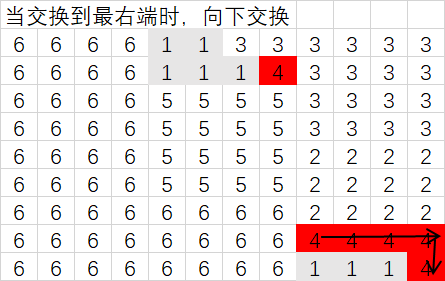
方向一:
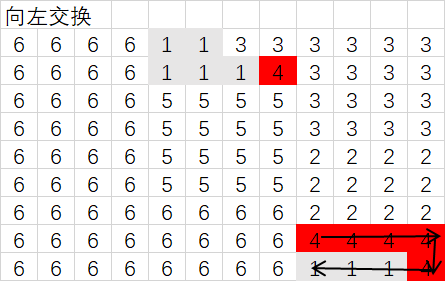
方向二:
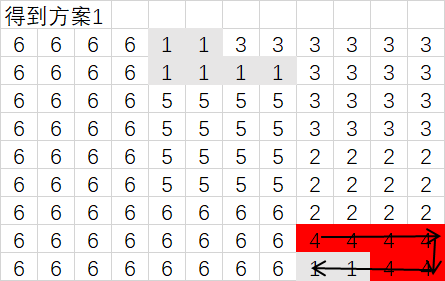
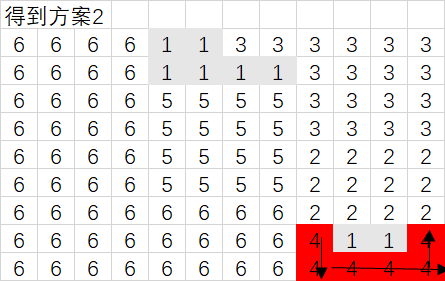
使用相同方法确定其他交换点的方案。该例共有3(交换点)*2(交换方向)=6种交换方案
(二)部门相邻判断
通常情况下,部门划分出若干栅格,但是栅格面积之和表示部门面积,不可分割。那么部门交换以后,需要判断部门是否为一个整体。若是一个整体,方案可行;否则,不可行。
处理方式为:抽象为多个区域的相邻或者相离判断,即区域之间的距离判断。假设,区域中心为所有栅格的重心,距离为折现距离。
2.1相邻判断
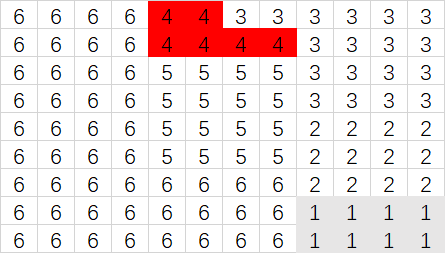
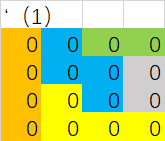
初始布局区域:
所有区域赋值为0:
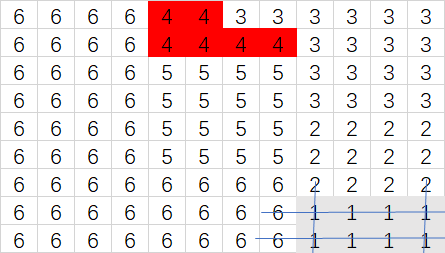
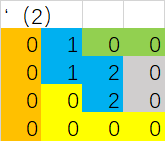
假设交换部门后,一部门划分为两块,其一赋值为1,另一区域为2:
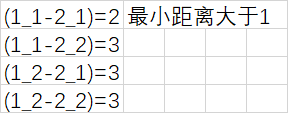
折线距离计算为:
2.2相离判断
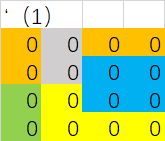
初始布局区域:
所有区域赋值为0:
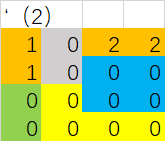
假设交换部门后,一部门划分为两块,其一赋值为1,另一区域为2:
折线距离计算为:
(三)代码
C++代码如下:
(考虑下再传…)
最后,感谢顾同学的指正与引导!
今天的文章物流设备及主要功能介绍_五种运输方式的设施设备分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/63047.html