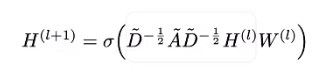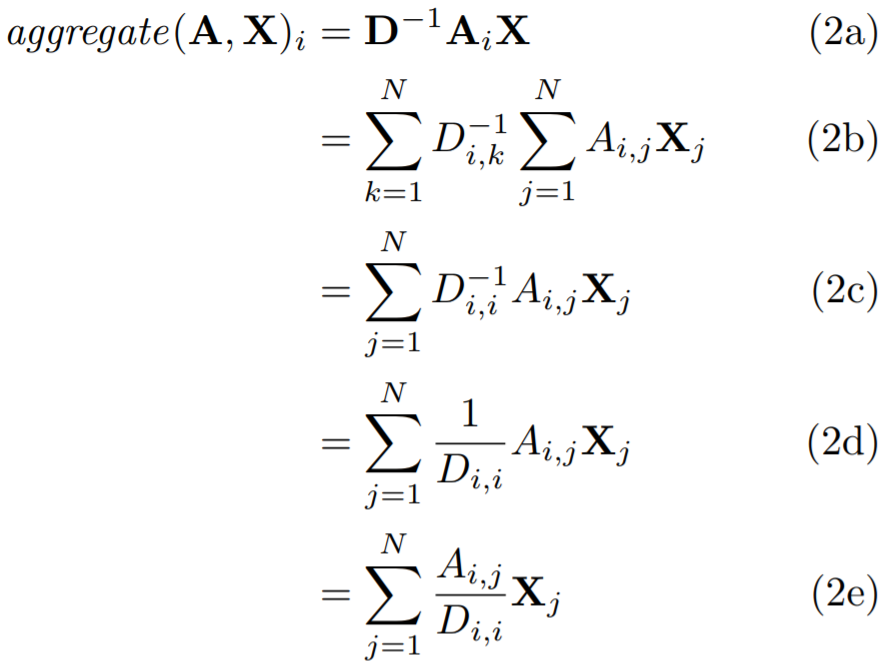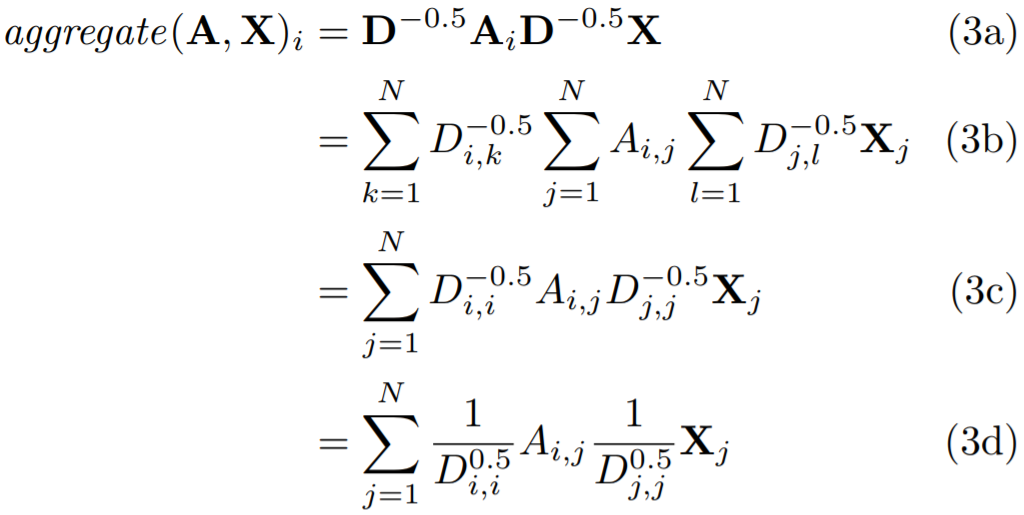文章目录
原文看这里:A High-Level Introduction to Graph Convolutional Networks
1 基本概念
1.1 图神经网络中的基本元素
一般的图中包含以下几种基本元素:
- 节点 v v v:(蓝色的点)
- 边 X ( u , v ) X_{(u,v)} X(u,v):(黑色的边,也就是节点 u , v u,v u,v之间的特征向量)
- 节点特征向量: X v X_v Xv
- 特征向量: h v k h_v^k hvk,代表节点 v v v在第 k k k次循环(第 k k k层)的特征向量。解释:其中每一个节点都有自己的特征,也就是说某个节点可用一个向量表示,可理解为普通神经网络中的隐藏节点,在收敛过程中权重会发生变化。
1.2 图神经网络学习的流程
1.2.1 图神经网络与随机游走的区别
随机游走模型是先按照一定规则生成节点序列,对这个节点序列进行embedding,再对embedding进行操作,得到后续的操作,如分类、匹配之类的。但是GNN则是一个端到端的模型,输入是Graph node,输出就是任务结果。
1.2.2 图神经网络的输入
更形式化地说,图卷积网络(GCN)是一个对图数据进行操作的神经网络。给定图 G = (V, E),GCN 的输入为:
- 一个输入维度为 N × F 0 N \times F^0 N×F0 的特征矩阵 X X X,其中 N N N 是图网络中的节点数而 F 0 F^0 F0 是每个节点的输入特征数。
- 一个图结构的维度为 N × N N \times N N×N 的矩阵表征,例如图 G 的邻接矩阵 A A A。
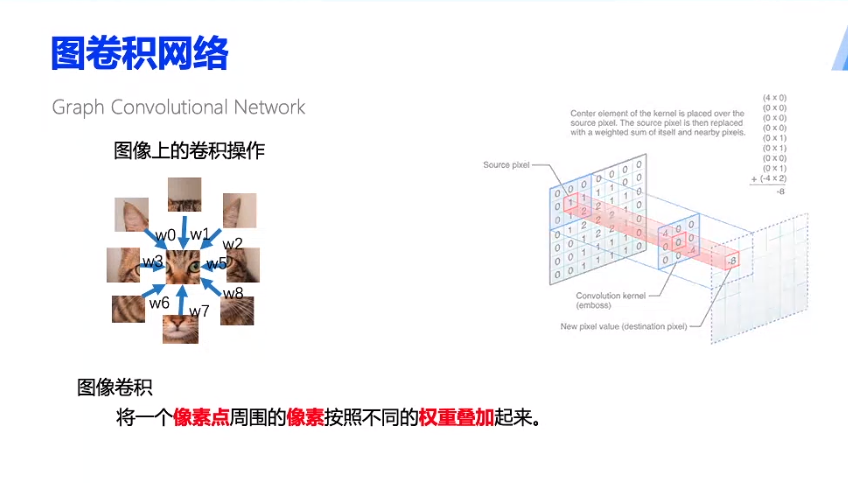
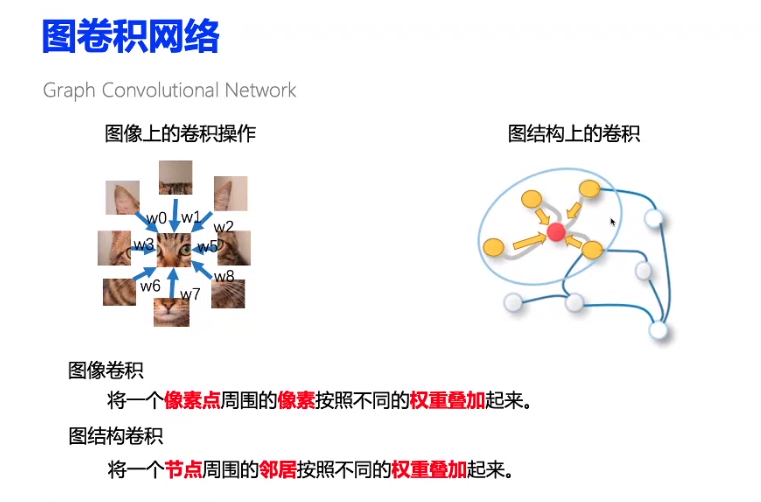
具体可类比图像的卷积:
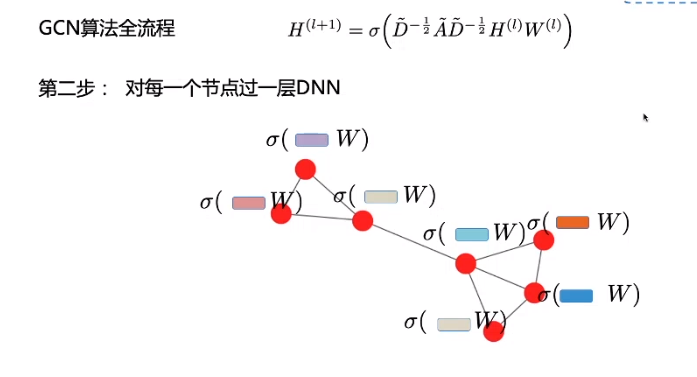
1.2.3 图神经网络的更新
1.2.3.1 直观印象
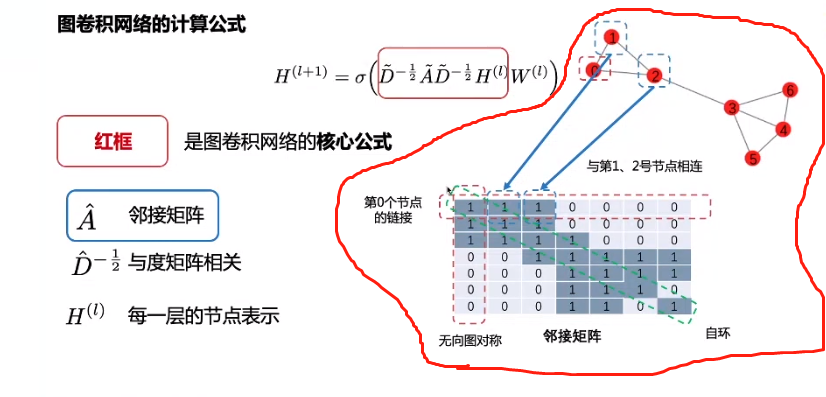
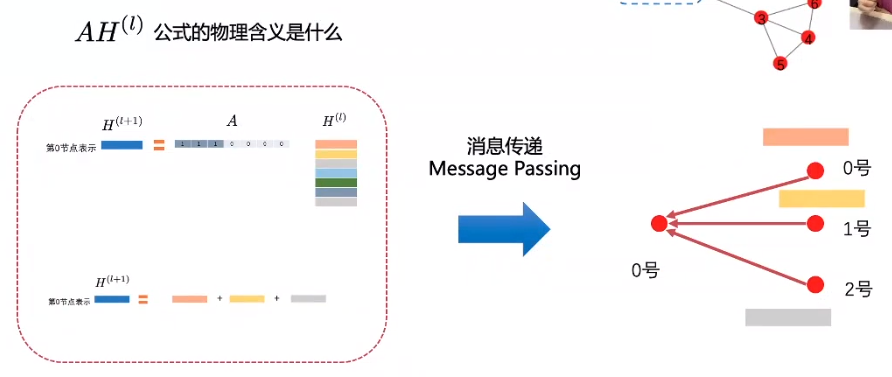
首先,GCN的计算公式长这样:
- 邻接矩阵,以右上角的节点为例,0与1,2都相连,因此,邻接矩阵中的第0行的第0、1、2列均为1,0行0列表示其自身相连,又因是无向图,因此关于主对角线对阵
- 度矩阵:按行求和,然后求倒数开根号
为了方便理解,先不考虑度矩阵(其实度矩阵可以看做是线性映射,将邻接矩阵映射到一个正交空间中,不影响其表达)
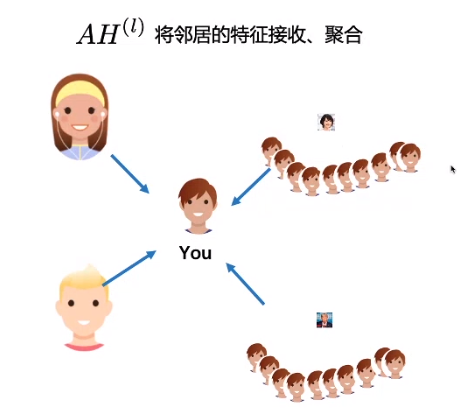
整个计算过程,可以看做:邻居节点把自身的信息发送给0号节点,可以看做是send操作,而对于0号节点来说,他怎么处理接受的信息,则可以看做是recv操作。
这里有个问题,就是当某个邻居节点有过多的边时,它所承载的信息过于庞大,可能会影响到目标节点信息的处理,具体例子如下:
在上图中,四个人给你做评价,两个好朋友和两个明星(你只是他们的粉丝,他们对粉丝的评价,所以你也会收到),但是因为特朗普的粉丝特别多,所以他携带的信息量特别大,这样的话,其实是不利于建模的。
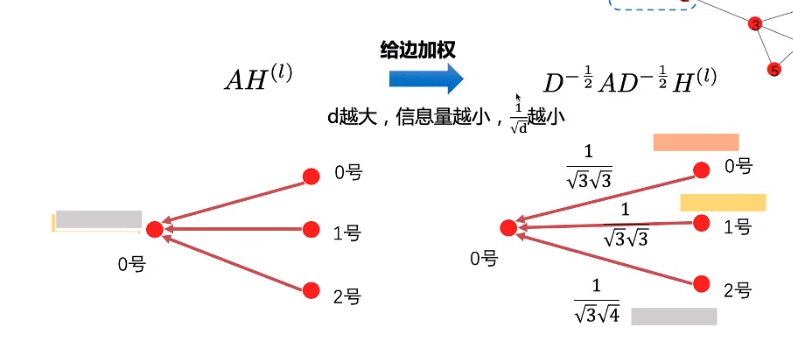
这个时候,度矩阵就上场了
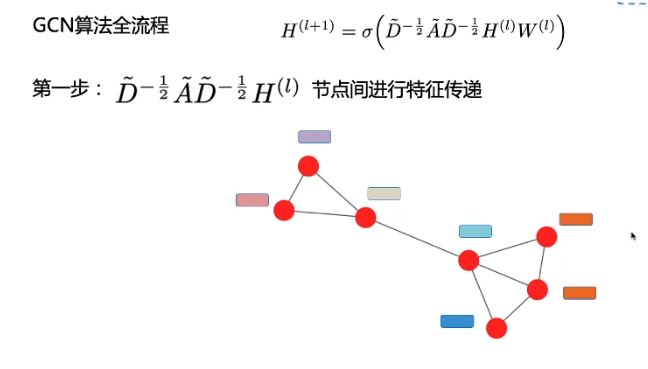
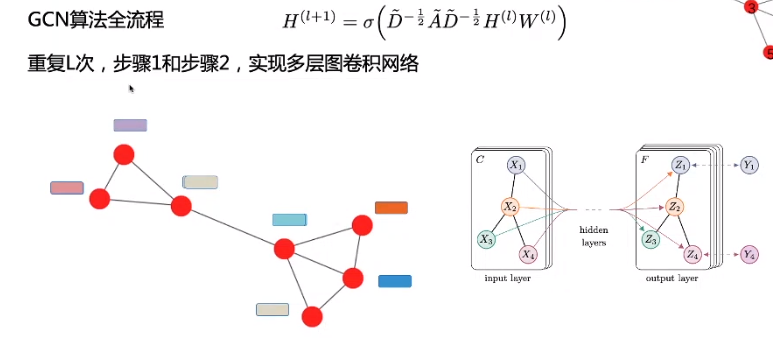
多层的图卷积:
1.2.3.2 理解
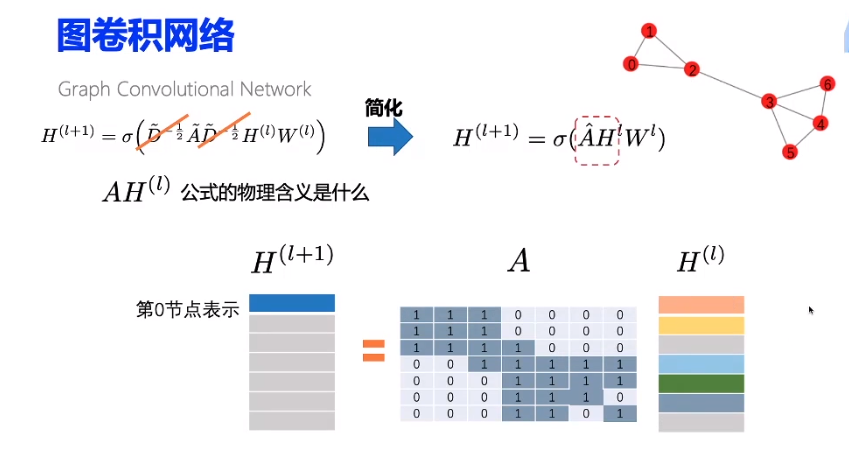
因此,GCN 中的隐藏层可以写作 H i = f ( H i − 1 , A ) ) H^i = f(H^{i-1}, A)) Hi=f(Hi−1,A))。其中, H 0 = X H^0 = X H0=X, f f f 是一种传播规则。每一个隐藏层 H i H^i Hi 都对应一个维度为 N × F i N \times F^i N×Fi 的特征矩阵,该矩阵中的每一行都是某个节点的特征表征。在每一层中,GCN 会使用传播规则 f f f 将这些信息聚合起来,从而形成下一层的特征。这样一来,在每个连续的层中特征就会变得越来越抽象。在该框架下,GCN 的各种变体只不过是在传播规则 f f f 的选择上有所不同 [1]。
1.2.3.1 图神经网络的传播方式1
f ( H i , A ) = σ ( A H i W i ) (1.1) f(H^i, A) = \sigma(AH^iW^i) \tag{1.1} f(Hi,A)=σ(AHiWi)(1.1)
其中, w i w^i wi是第 i i i层的权重矩阵, σ \sigma σ是非线性激活函数(sigmoid,relu)等。权重矩阵的维度为 F i × F i + 1 F^i \times F^{i+1} Fi×Fi+1,即权重矩阵第二个维度的大小决定了下一层的特征数。
那么,当迭代次数为1时,参数配置如下:
- i = 1 i=1 i=1
- σ \sigma σ函数是所有节点共用的函数。原文中是(identity function)
- 权重的限制条件为:
A H 0 W 0 = A X W 0 = A X (1.1.1) AH^0W^0=AXW^0=AX\tag{1.1.1} AH0W0=AXW0=AX(1.1.1)
上式中, A A A为邻接矩阵(可以为其他函数), H i H^i Hi第 i i i次迭代之后节点的状态, H 0 H^0 H0为原始输入 X X X,在上述约束条件下,激活函数 σ \sigma σ为线性函数。
1.2.3.2 图神经网络的传播方式2
这种传播方式的链接地址。
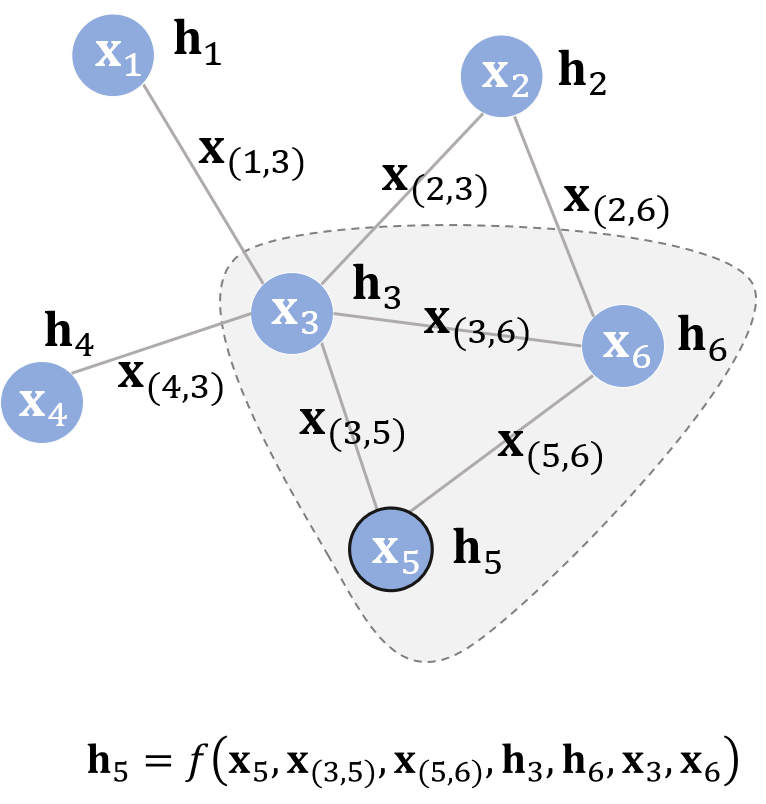
同之前的图结构一样,每个节点都有自己的特征 X v X_v Xv与标签 t v t_v tv。给定部分有标签的图 G G G,目标是通过这些有标签的点去预测无标签点的标签。其中,在演化过程中,获得每个结点的图感知的隐藏状态 h v h_v hv(state embedding),这就意味着:对于每个节点,它的隐藏状态包含了来自邻居节点的信息。那么,如何让每个结点都感知到图上其他的结点? GNN通过迭代式更新所有结点的隐藏状态来实现,在 t + 1 t+1 t+1时刻,结点 V V V的隐藏状态按照如下方式更新:
h v t + 1 = f ( X v , X c o [ v ] , h n t e [ v ] , X n e [ v ] ) h_v^{t+1}=f(X_v, X_co[v], h^t_ne[v], X_ne[v]) hvt+1=f(Xv,Xco[v],hnte[v],Xne[v])
上式中,函数 f f f的作用与4个自变量的意义分别为:
- f f f: 是隐藏状态的状态更新函数(局部转移函数(local transaction function))。该函数用于对与目标结点相邻节点的更新,是一个局部共享的函数。
- X c o [ v ] X_co[v] Xco[v]: 与结点 v v v相邻的边的特征;
- X n e [ v ] X_ne[v] Xne[v]: 结点 v v v的邻居结点的特征;
- h n t e [ v ] h^t_ne[v] hnte[v]:指邻居结点在 t t t时刻的隐藏状态
举个栗子:
不断地利用当前时刻邻居结点的隐藏状态作为部分输入来生成下一时刻中心结点的隐藏状态,直到每个结点的隐藏状态变化幅度很小,整个图的信息流动趋于平稳。至此,每个结点都“知晓”了其邻居的信息。状态更新公式仅描述了如何获取每个结点的隐藏状态,除它以外,我们还需要另外一个函数 g g g(局部输出函数(local output function)) 来描述如何适应下游任务(也就是这个节点具体要干啥:输出本节点的标签?还是做分类什么的)。
GNN的输出通过**状态 h v h_v hv和特征 x v x_v xv**给激活函数 g g g进行计算。
O v = g ( h v , x v ) O_v=g(h_v,x_v) Ov=g(hv,xv)
整个图的损失函数为:
l o s s = ∑ i = 1 p ( t i − o i ) loss=\sum_{i=1}^p(t_i-o_i) loss=i=1∑p(ti−oi)
可以通过反向传播算法进行优化。
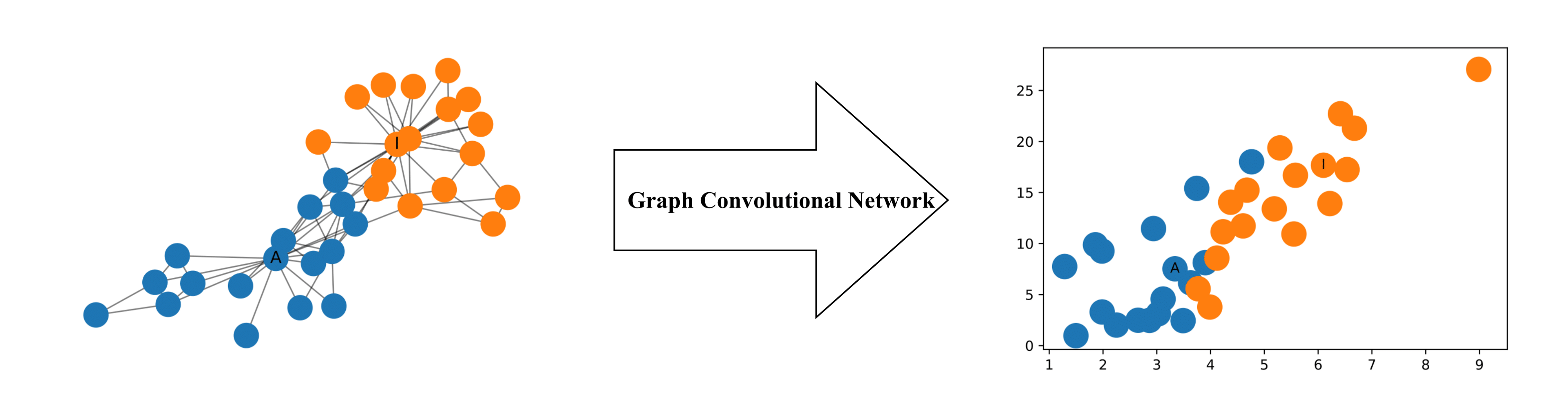
2. 图神经网络的实例
下图展示了每个节点都由2维数据构成的图结构。即使没有经过任何训练,2维的特征表征也存储了网络中节点的相对邻近性。
该部分主要参考参考文献中《手写图神经网络系列》—— 感谢大神们!!!
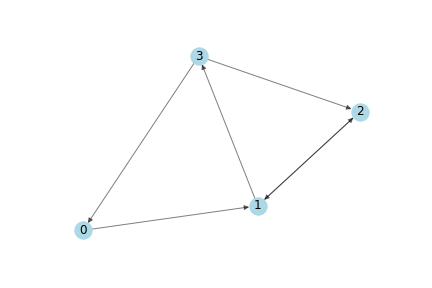
假设图的结构是这样的。
那么,邻接矩阵的定义如下,箭头指向的点为相邻节点。
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
每一个节点的特征假设为2维的
In [3]: X = np.matrix([
[i, -i]
for i in range(A.shape[0])
], dtype=float)
X
Out[3]: matrix([
[ 0., 0.],
[ 1., -1.],
[ 2., -2.],
[ 3., -3.]
])
在图上使用传播规则,根据公式1.1.1有:
In [6]: A * X
Out[6]: matrix([
[ 1., -1.],
[ 5., -5.],
[ 1., -1.],
[ 2., -2.]]
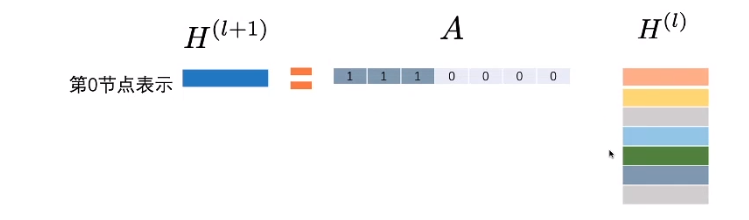
其具体含义为:每一个节点(每一行)的值都是其相邻节点特征的和。根据如何通俗的理解卷积可知,卷积的本质其实就是加权求和。换句话说,在这个例子中,最后的结果就是所有节点聚合的结果。
但是,上述计算方法有以下两个问题:
- 节点聚合的结果中,仅仅包含的是相邻节点的特征,并没有包括节点自身的特征信息。因此只有具有自环(self-loop)的节点才会在该聚合中包含自己的特征。
- 度大的节点在其特征表征中将具有较大的值,度小的节点将具有较小的值(说白了,就是可能出现有的点有一个相邻节点,而有的点则可能连接了1000个点,那这样的话。。。)。这可能会导致梯度消失或梯度爆炸 [1, 2],也会影响随机梯度下降算法(随机梯度下降算法通常被用于训练这类网络,且对每个输入特征的规模(或值的范围)都很敏感)。
2.1 添加自身特征
直接为每个节点添加一个自环,所以修改邻接矩阵A为:
I = np.matrix(np.eye(A.shape[0]))
A_hat = A + I
''' I's Value matrix([ [1., 0., 0., 0.], [0., 1., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 1.] ]) Ahat's Value matrix([ [1, 1, 0, 0], [0, 1, 1, 1], [0, 1, 1, 0], [1, 0, 1, 1] ]) '''
A_hat * X
''' Out[8]: matrix([ [ 1., -1.], [ 6., -6.], [ 3., -3.], [ 5., -5.]]) '''
2.2 归一化
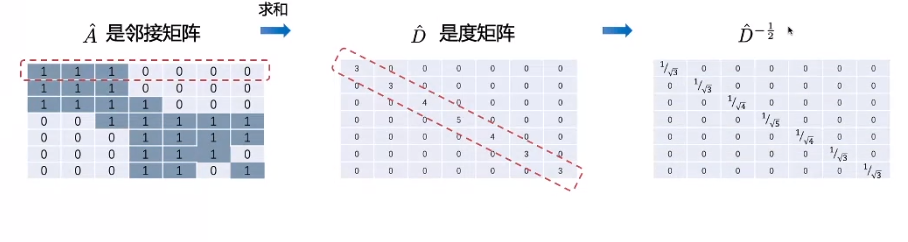
在实数空间中,实数矩阵的逆其实可以理解成分子。因此,将邻接矩阵A与度矩阵D的逆相乘,对其进行变换,从而通过节点的度对特征表征进行归一化。
啥是**度矩阵?**就是用矩阵表示每个节点的连接的数目。
上图中,度矩阵为:
D = np.array(np.sum(A, axis=0))[0]
D = np.matrix(np.diag(D))
''' matrix([ [1., 0., 0., 0.], [0., 2., 0., 0.], [0., 0., 2., 0.], [0., 0., 0., 1.] ]) '''
变换之后的结果为:
In [10]: D**-1 * A
Out[10]: matrix([
[0. , 1. , 0. , 0. ],
[0. , 0. , 0.5, 0.5],
[0. , 0.5, 0. , 0. ],
[0.5, 0. , 0.5, 0. ]
])
执行公式1.1.1有:
In [11]: D**-1 * A * X
Out[11]: matrix([
[ 1. , -1. ],
[ 2.5, -2.5],
[ 0.5, -0.5],
[ 2. , -2. ]
])
2.3 添加权重
D_hat是 A_hat = A + I对应的度矩阵,即具有强制自环的矩阵 A 的度矩阵。
In [45]: W = np.matrix([
[1, -1],
[-1, 1]
])
D_hat**-1 * A_hat * X * W
Out[45]: matrix([
[ 1., -1.],
[ 4., -4.],
[ 2., -2.],
[ 5., -5.]
])
如果我们想要减小输出特征表征的维度,我们可以减小权重矩阵 W 的规模:
In [46]: W = np.matrix([
[1],
[-1]
])
D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
[4.],
[2.],
[5.]]
)
2.4 添加激活函数
保持特征表征的维度,并应用 ReLU 激活函数。
In [51]: W = np.matrix([
[1, -1],
[-1, 1]
])
relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
[4., 0.],
[2., 0.],
[5., 0.]])
3. 聚合方法
第2节中使用的方法是基于非谱的,也就是利用了图中节点的空间信息,目前,研究人员Kipf 和 Welling提出了基于谱的图卷积方式。
这种更新方式如下:
f ( X , A ) = σ ( D − 0.5 A ^ D − 0.5 X W ) f(X,A)=\sigma(D^{-0.5}\hat{A}D^{-0.5}XW) f(X,A)=σ(D−0.5A^D−0.5XW)
与之前更新节点方式不同之处在于,聚合各节点的方式。
各节点之间的连接方式:求和、求均值、求谱
3.1 和方法
按照定义,某一节点 i i i的聚合值应该为: ∑ j = 1 N A i , j X j \sum_{j=1}^NA_{i,j}X_j ∑j=1NAi,jXj,用矩阵可表示为:
A i X \boldsymbol{A_iX} AiX
3.2 均值方法
为简单起见,使用的矩阵为邻接矩阵,没有加上考虑自身特征的信息。
这种计算方式同求和一样,也依赖于邻接矩阵A和度矩阵。
3.3 谱方法
在平均值方法中,我们使用邻接矩阵A的度矩阵来规则化邻接矩阵A,然而,在谱方法中,将度矩阵开 − 0.5 -0.5 −0.5次方后,左右乘邻接矩阵A,与均值方法相同,都起到了正则化的作用。只是其正则化方法略有不同,度越低,正则化后权重越大;度越大,正则化后权重越小。
However, the spectral rule weighs neighbor in the weighted sum higher if they have a low-degree and lower if they have a high-degree. This may be useful when low-degree neighbors provide more useful information than high-degree neighbors.
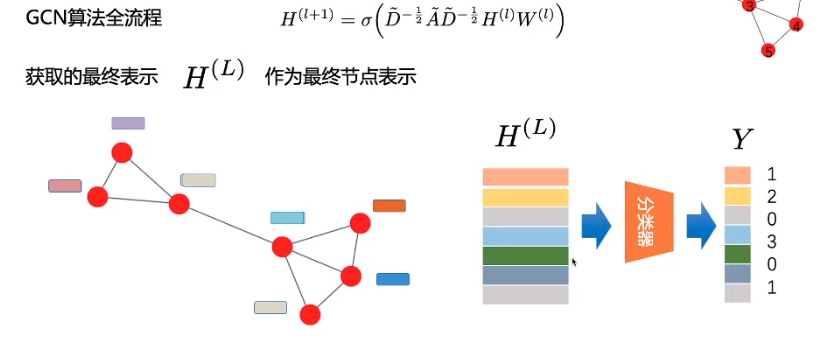
4. 应用——半监督分类
在半监督学习中,我们想要把这个模型使用于同时具有标签和非标签的例子。也就是说,我们假设知道所有的点(transductive setting),但是不知道所有点所对应的标签,只知道 一部分。
因此,GCN的训练过程如下:
- 完成GCN网络前向传播过程
- 使用激活函数
- 通过计算已知节点的cross entropy loss
- 利用反向传播算法更新每一层的权重。
下文实现的例子是来自于手写图神经网络系列2:Semi-Supervised Learning with Spectral Graph Convolutions。数据大意是一个club,主管和教练闹掰了,俩人各自成立一个小团体,现在要预测一下原本club中的会员们分别会参加哪边的阵营。
注:数据来源于这里。
from collections import namedtuple, OrderedDict
from networkx import read_edgelist, set_node_attributes
import pandas as pd
import numpy as np
from networkx import to_numpy_array, shortest_path_length
from torch import nn
from time import sleep
import torch.nn.functional as F
import torch.optim as optim
import torch
from sklearn.metrics import classification_report
np.random.seed(1)
torch.manual_seed(1)
def load_karate_club():
# 读取网络中所有边的信息,构建网络
network = read_edgelist('data/karate.edgelist', nodetype=int)
# 读取每个节点的信息
attributes = pd.read_csv('data/karate.attributes.csv', index_col=['node'])
# 将节点信息写入网络中
for attribute in attributes.columns.values:
set_node_attributes(
network,
values=pd.Series(attributes[attribute], index=attributes.index).to_dict(),
name=attribute
)
X_train, y_train = map(np.array, zip(*[
([node], data['role'] == 'Administrator')
for node, data in network.nodes(data=True) if data['role'] in {
'Administrator', 'Instructor'}
])
)
X_test, y_test = map(np.array, zip(*[
([node], data['community'] == 'Administrator')
for node, data in network.nodes(data=True)
if data['role'] == 'Member'
]))
DataSet = namedtuple('DataSet', field_names=['X_train', 'y_train', 'X_test', 'y_test', 'network'])
return DataSet(
X_train, y_train,
X_test, y_test,
network)
def format_data(zkc):
adjenct_matrix = to_numpy_array(zkc.network)
X_train = zkc.X_train.flatten()
# one-hot 标准化数据
y_train = zkc.y_train.astype(int)
# y_train = np.eye(y_train_index.shape[0])[y_train_index]
X_test = zkc.X_test.flatten()
# one-hot 标准化数据
y_test = zkc.y_test.astype(int)
# y_test = np.eye(y_test_index.shape[0])[y_test_index]
return X_train, y_train, X_test, y_test, adjenct_matrix
class UnitTest(object):
def spectral_rule(self):
A = np.array([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]
])
A = torch.Tensor(A)
layer = SpectralRule(A, 4, 2)
print(layer(A))
def logistic_regressor(self):
A = np.array([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]
])
A = torch.Tensor(A)
layer = LogisticRegressor(4, A.size()[0])
print(layer(A))
def check_model_structure(self):
A = np.array([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]
])
X = np.array([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]
])
model = build_model(A, X)
print(model)
def check_model(self):
zkc = load_karate_club()
X_train, y_train, X_test, y_test, adjenct_matrix = format_data(zkc)
# 自身特征作为输入变量的情况
X_1 = np.eye(adjenct_matrix.shape[0])
X_1 = torch.Tensor(X_1)
# model = build_model(adjenct_matrix, X_1)
# print(model(X_1))
# 自身特征+已知节点(不同类)后的特征
X_2 = np.zeros((adjenct_matrix.shape[0], 2))
node_distance_instructor = shortest_path_length(zkc.network, target=33)
node_distance_administrator = shortest_path_length(zkc.network, target=0)
for node in zkc.network.nodes():
X_2[node][0] = node_distance_administrator[node]
X_2[node][1] = node_distance_instructor[node]
X_2 = torch.Tensor(X_2)
X_2 = torch.cat((X_1, X_2), 1)
adjenct_matrix = torch.Tensor(adjenct_matrix)
model_2 = build_model(adjenct_matrix, X_2)
print(model_2(X_2))
# 定义图聚合层
class SpectralRule(nn.Module):
def __init__(self, adjenct_matrix, in_units, out_units, activation='relu'):
super(SpectralRule, self).__init__()
# 构造单位矩阵 I,表示图节点中加上自身的特征信息
I = torch.eye(adjenct_matrix.size()[0])
# 计算自身特征信息与相邻节点特征信息之和
adjenct_matrix_hat = adjenct_matrix + I
# 计算每一个节点的所有度,mxnet和pytorch的展开的维度不一样
node_degree = adjenct_matrix_hat.sum(axis=1)
# 借助度信息,构造度矩阵(是一个对角矩阵)
node_degree_inv = torch.diag(node_degree ** -0.5)
# 计算归一化后的邻接矩阵
A_hat = node_degree_inv * adjenct_matrix_hat * node_degree_inv
# 初始化权重值
# init_weight = nn.init.uniform_(
# torch.empty(in_units, out_units),
# -1, 1
# )
init_weight = np.random.uniform(-1, 1, (in_units, out_units))
init_weight = torch.Tensor(init_weight)
self.in_units, self.out_units = in_units, out_units
self.A_hat = torch.Tensor(A_hat)
# 将权重加入自动求导列表
# self.A_hat = nn.Parameter(torch.Tensor(A_hat))
self.weight = nn.Parameter(init_weight)
if activation == 'identity':
self.activation = lambda X: X
elif activation == 'tanh':
self.activation = torch.tanh
else:
self.activation = torch.relu
def forward(self, X):
aggregate = self.A_hat.mm(X)
propagate = torch.tanh(
aggregate.mm(self.weight)
)
return propagate
class LogisticRegressor(nn.Module):
def __init__(self, in_units, sample_nums):
super(LogisticRegressor, self).__init__()
# 初始化权重值
# init_weight = nn.init.uniform_(
# torch.empty(1, in_units),
# -1, 1
# )
# init_bias = nn.init.uniform_(
# torch.empty(sample_nums, 1),
# -1, 1
# )
init_weight = np.random.uniform(-1, 1, (1, in_units))
init_weight = torch.Tensor(init_weight)
init_bias = np.random.uniform(-1, 1, (sample_nums, 1))
init_bias = torch.Tensor(init_bias)
# 将偏置项b扩展为节点的数目
# init_bias = init_bias.repeat(sample_nums, 1)
# 将权重加入自动求导列表
self.weight = nn.Parameter(init_weight)
self.bias = nn.Parameter(init_bias)
def forward(self, X):
y = X.mm(self.weight.T) + self.bias
# print("y")
# print(y)
# print("weight")
# print(self.weight)
# print("bias")
# print(self.bias)
return torch.sigmoid(y)
def build_model(A, X):
# 构建特征网络部分
net_dict = OrderedDict()
## 特征网络配置参数
### 元组中第一个元素为该层隐藏单元的数量,第二个元素为激活函数
### Format: (units in layer, activation function)
hidden_layer_specs = [(4, 'tanh'), (2, 'tanh')]
in_units = X.size()[1]
### 开始构建特征网络
for i, (layer_size, activation_func) in enumerate(hidden_layer_specs):
layer = SpectralRule(
A, in_units=in_units, out_units=layer_size,
activation=activation_func
)
net_dict['feature_'+str(i)] = layer
in_units = layer_size
# 构建分类网络部分
net_dict['classifier'] = LogisticRegressor(in_units, X.size()[0])
# 转化为torch类型网络
model = torch.nn.Sequential(net_dict)
# Print model's state_dict
print("Model's state_dict:")
for param_tensor in model.state_dict():
print(param_tensor, "\t", model.state_dict()[param_tensor].size())
# exit(32)
return model
def train(model, X_train, y_train, graph, epochs):
model.train()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=1)
for e in range(1, epochs + 1):
cum_preds = []
cum_loss = 0
for i, x in enumerate(X_train):
labels = np.array(y_train)[i]
labels = torch.from_numpy(np.array([labels])).type(torch.FloatTensor)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = model(graph)[x]
loss = F.binary_cross_entropy(outputs, labels)
loss.backward()
optimizer.step()
cum_loss += loss.item()
cum_preds.append(outputs.item())
if (e % (epochs // 10)) == 0:
print(f"Epoch {e}/{epochs} -- Loss: {cum_loss: .4f}")
print(cum_preds)
def predict(model, X, nodes):
model.eval()
with torch.no_grad():
preds = model(X)[nodes].numpy().flatten()
print(preds)
return np.where(preds >= 0.5, 1, 0)
def run():
zkc = load_karate_club()
X_train, y_train, X_test, y_test, adjenct_matrix = format_data(zkc)
# 两种输入数据
## 自身特征作为输入变量的情况
X_1 = np.eye(adjenct_matrix.shape[0])
X_1 = torch.Tensor(X_1)
adjenct_matrix = torch.Tensor(adjenct_matrix)
model_1 = build_model(adjenct_matrix, X_1)
# print(X_1)
# print(adjenct_matrix)
# print("======================")
# print(model(X_1))
## 自身特征+已知节点(不同类)后的特征
X_2 = np.zeros((adjenct_matrix.shape[0], 2))
node_distance_instructor = shortest_path_length(zkc.network, target=33)
node_distance_administrator = shortest_path_length(zkc.network, target=0)
for node in zkc.network.nodes():
X_2[node][0] = node_distance_administrator[node]
X_2[node][1] = node_distance_instructor[node]
X_2 = torch.Tensor(X_2)
X_2 = torch.cat((X_1, X_2), 1)
adjenct_matrix = torch.Tensor(adjenct_matrix)
model = build_model(adjenct_matrix, X_2)
# print(X_2)
# print(model(X_2))
train(model, X_train, y_train, X_2, epochs=250)
y_pred_1 = predict(model, X_2, X_test)
print(y_test)
print(y_pred_1)
print(classification_report(y_test, y_pred_1))
def test():
test_obj = UnitTest()
test_obj.spectral_rule()
test_obj.logistic_regressor()
# test_obj.check_model()
if __name__ == '__main__':
run()
参考文献
- Tensorflow版本的图卷积神经网络
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一)
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (三)
- 手写图神经网络系列1:A High-Level Introduction to Graph Convolutional Networks
- 手写图神经网络系列2:Semi-Supervised Learning with Spectral Graph Convolutions
- 来自清华大神的详细解读
- 如何通俗的理解卷积
- Keras版本的图卷积神经网络
- 图卷积的keras实现2
- 利用图神经网络处理问题的一般化流程
- A tutorial on Graph Convolutional Neural Networks
- 图卷积神经网络相关资源
- 图神经网络论文必读列表-github
- 图神经网络论文必读列表
今天的文章4 图神经网络—— 基本概念与手写code分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/63573.html