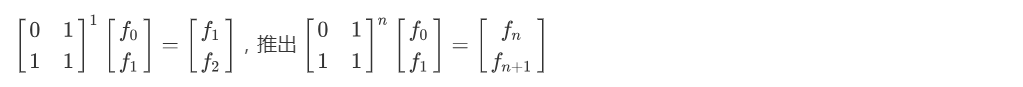WHUT第五周训练整理
写在前面的话:我的能力也有限,错误是在所难免的!因此如发现错误还请指出一同学习!
索引
(难度由题目自身难度与本周做题情况进行分类,仅供新生参考!)
一、easy:02、05、07、14、15、17
二、medium:04、06、08、09、10、12、13、16
三、hard:01、11、18
四、乱入的二分图:03
本题解报告大部分使用的是C++语言,在必要的地方使用C语言解释。
声明:本周题目的难度较之间几周的题目有所提升,这里我只给出我自己的解法,肯定还有其他可能更优的解法,有兴趣的同学可以多了解了解。
一、easy
1002:Hanoi Tower Troubles Again!(打表)
题意:有 n n n 根柱子,有无数个小球(编号从 1 1 1 开始)可以套在柱子上,对于一个空的柱子可以放任意的小球,对于一个非空的柱子,如果当前的小球的编号 + 柱子顶部小球的编号 = 平方数,那么可以放在上面,否则只能套在新的空柱子上。现在问 n n n 根柱子最多可以套多少个小球?
分析:发现 n n n 很小,通过打表发现 50 50 50 的 n n n 最多只能处理 1299 1299 1299 个小球,因此我这里就对于每个 n n n 都简单遍历 1 ∼ 1299 1\sim1299 1∼1299 模拟一下 n n n 根柱子能处理的最多的小球就可以了。
Code:
const int MAXN = 50 + 10;
int arr[MAXN];
int main()
{
int T, n;
cin >> T;
while (T--)
{
cin >> n;
int cnt = 0;
for (int i = 1; i <= 1300; i++) // 简单遍历
{
int j;
for (j = 0; j < cnt; j++) // 在已有的柱子中尝试套上当前的小球
{
int now = arr[j] + i;
int tmp = sqrt(now);
if (tmp * tmp == now) // 是平方数则套上
{
arr[j] = i;
break;
}
}
if (j == cnt) // 所有柱子都套不上则另起一个柱子
{
arr[cnt++] = i;
}
if (cnt == n + 1) // 如果用的柱子超过了n则输出答案
{
cout << i - 1 << endl;
break;
}
}
}
return 0;
}
1005:Can you solve this equation?(数学+二分)
题意:给定 Y Y Y,求 Y = 8 x 4 + 7 x 3 + 2 x 2 + 3 x + 6 Y= 8x^4+7x^3+2x^2+3x+6 Y=8x4+7x3+2x2+3x+6 在 x ∈ [ 0 , 100 ] x\in[0,100] x∈[0,100] 中的解。
分析:设 f ( x ) = 8 x 4 + 7 x 3 + 2 x 2 + 3 x + 6 f(x)= 8x^4+7x^3+2x^2+3x+6 f(x)=8x4+7x3+2x2+3x+6,则 f ′ ( x ) = 32 x 3 + 21 x 2 + 4 x + 3 f'(x) = 32x^3+21x^2+4x+3 f′(x)=32x3+21x2+4x+3。
当 x ∈ [ 0 , 100 ] x\in[0,100] x∈[0,100] 时,满足 f ′ ( x ) > 0 f'(x)>0 f′(x)>0,即在 [ 0 , 100 ] [0,100] [0,100] 中 f ( x ) f(x) f(x) 单调递增,使用二分法求解即可。
Notice:注意精度问题!不论是二分还是三分,尽量输出 m i d mid mid 值而不是 l e f t left left 或者 r i g h t right right 。
Code:
const double eps = 1e-5;
double f(double x)
{
return 8 * pow(x, 4) + 7 * pow(x, 3) + 2 * pow(x, 2) + 3 * x + 6;
}
double solve(double y)
{
double l = 0, r = 100;
while (fabs((f(l) - y) - (f(r) - y)) >= eps)
{
double mid = (l + r) / 2;
if (f(mid) < y)
{
l = mid;
}
else
{
r = mid;
}
}
return l;
}
int main()
{
int T;
cin >> T;
while (T--)
{
double y;
cin >> y;
if (f(0) > y || f(100) < y) // 如果低于最小值或者大于最大值,则无解
{
cout << "No solution!" << endl;
}
else
{
cout << fixed << setprecision(4) << solve(y) << endl;
}
}
return 0;
}
1007:Strange fuction(数学+三分)
题意:给定 y y y,求函数 F ( x ) = 6 x 7 + 8 x 6 + 7 x 3 + 5 x 2 − y ∗ x F(x)=6x^7+8x^6+7x^3+5x^2-y*x F(x)=6x7+8x6+7x3+5x2−y∗x 在 [ 0 , 100 ] [0,100] [0,100] 上的最小值。
分析:求导 F ′ ( x ) = 42 x 6 + 48 x 5 + 21 x 2 + 10 x − y F'(x) = 42x^6+48x^5+21x^2+10x-y F′(x)=42x6+48x5+21x2+10x−y
再求导 F ′ ′ ( x ) = 252 x 5 + 240 x 4 + 42 x + 10 F”(x) = 252x^5+240x^4+42x+10 F′′(x)=252x5+240x4+42x+10 得 F ′ ′ ( x ) > 0 F”(x) > 0 F′′(x)>0 当 x ∈ [ 0 , 100 ] x\in[0,100] x∈[0,100] 。
故 F ′ ( x ) F'(x) F′(x) 在 [ 0 , 100 ] [0,100] [0,100] 上单调递增,又因 F ′ ( 0 ) = − y < 0 F'(0) = -y < 0 F′(0)=−y<0,因此 F ′ ( x ) F'(x) F′(x) 的值由负到正。
因此函数 F ( x ) F(x) F(x) 先减后增,是在 [ 0 , 100 ] [0,100] [0,100] 上的凹函数,上三分即可。
Code:
const double eps = 1e-6;
double y;
double f(double x) // 函数值
{
return 6 * pow(x, 7) + 8 * pow(x, 6) + 7 * pow(x, 3) + 5 * x * x - y * x;
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> y;
double l = 0, r = 100;
while (r-l >= eps) // 三分确定答案
{
double lm = (r + l) / 2;
double rm = (lm + r) / 2;
if (f(lm) < f(rm)) // 左边<右边,在凹函数中舍弃右边
{
r = rm;
}
else // 否则舍弃左边
{
l = lm;
}
}
cout << fixed << setprecision(4) << f(l) << endl;
}
return 0;
}
1014:Starship Hakodate-maru(暴力枚举)
题意:有 n n n 吨的货物需要装入容器,现在有两种容器,第一种只能装进 i 3 i^3 i3 吨的货物,第二种只能装进 j ( j + 1 ) ( j + 2 ) ) 2 \frac{j(j+1)(j+2))}{2} 2j(j+1)(j+2)) 吨的货物,现在求利用这两种容器最多能装入多少货物?注意不能超过 n n n 。
分析: n n n 最多是 151200 151200 151200,直接双重循环枚举 i , j i,j i,j 更新答案即可。详见代码。
Code:
int main()
{
int n;
while (cin >> n, n)
{
int ans = 0;
for (int i = 0; i * i * i <= n; i++) // 枚举i
{
for (int j = 0; j * (j + 1) * (j + 2) / 6 <= n; j++) // 枚举j
{
int sum = i * i * i + j * (j + 1) * (j + 2) / 6; // 当前容器装入的货物吨数
if (sum <= n) // 保证不超过n
{
ans = max(ans, sum); // 更新答案
}
}
}
cout << ans << endl; // 输出
}
return 0;
}
1015:Pseudoprime numbers(素数判断+快速幂)
题意:给定 p p p 以及 a a a,现在问 p p p 是否是基于 a a a 的伪素数。
分析:首先 p p p 本身不能是素数,其次要满足 a p ≡ a ( m o d p ) a^p \equiv a \pmod{p} ap≡a(modp)。比较基础比较套路,数据范围比较大, p ∈ [ 3 , 1 e 9 ] p \in [3,1e9] p∈[3,1e9],首先判断素数可以在 O ( n ) O(\sqrt{n}) O(n) 内完成,而求 a p a^p ap 模 p p p 的结果可以用快速幂 O ( l o g 2 n ) O(log_2n) O(log2n) 完成。详见代码。
Code:
long long poww(int a, int n, int mod) // 快速幂,取模
{
long long ans = 1;
long long pingfang = a;
while (n != 0)
{
if (n % 2 == 1)
{
ans = ans % mod * pingfang % mod; // 遇到二进制中的1时 说明需要取
}
pingfang = pingfang % mod * pingfang % mod; // pingfang不断往上翻
n /= 2;
}
return ans % mod;
}
int isPrime(int x) // 判断素数
{
for (int i = 2; i <= sqrt(x); i++)
{
if (x % i == 0)
return 0;
}
return 1;
}
int main()
{
int p, a;
while (cin >> p >> a, p + a)
{
if (isPrime(p) || poww(a, p, p) != a) // 两个条件
{
cout << "no" << endl;
}
else
{
cout << "yes" << endl;
}
}
return 0;
}
1017:Shopping(暴力+map)
题意:给 n n n 家店,一开始每家店的出售价格都是 0 0 0,之后 m m m 天中每天都给出这 n n n 家店的涨价数值(给出的顺序不固定),问 m m m 天中每天涨价后名为 m e m o r y memory memory 的店的价格排名是多少。第 i i i 家店价格排名定义为如果有 t t t 家店的价格比 i i i 店贵,那么第 i i i 家店的排名就是 t + 1 t+1 t+1 。
分析: n < = 1 e 4 , m ∈ [ 1 , 50 ] n <= 1e4, m \in [1, 50] n<=1e4,m∈[1,50] 。看这数据范围可以直接直接进行暴力就可以了,每天更新每家店的价格,然后遍历找到比 m e m o r y memory memory 店价格高的店数量即可,因为给出的顺序不固定,所以使用 m a p map map 来确定索引。
Code:
const int MAXN = 1e4 + 10;
int n, m;
map<string, int> id;
int arr[MAXN];
int main()
{
while (cin >> n)
{
memset(arr, 0, sizeof(arr)); // 清空店铺价格
id.clear(); // 清空map
int index = 0; // 用于确定店铺的索引
for (int i = 0; i < n; i++)
{
string str;
cin >> str;
id[str] = index++; // 给每家店分配索引
}
cin >> m;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
int s;
string str;
cin >> s >> str;
arr[id[str]] += s; // 给每家店涨价
}
int now = arr[id["memory"]];
int rk = 1;
for (int j = 0; j < n; j++) // 遍历确定排名
{
if (arr[j] > now)
rk++;
}
cout << rk << endl;
}
}
return 0;
}
二、medium
1004:Turn the corner(计算几何+三分)
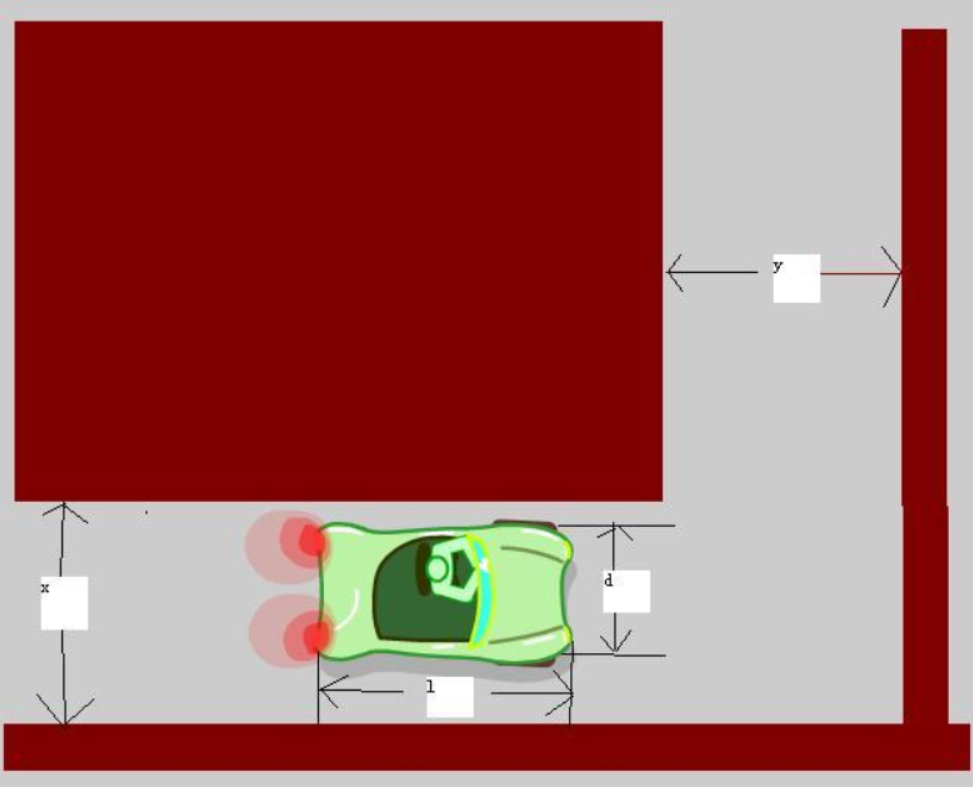
题意:给定车长 l l l 、车宽 d d d、所处街道宽度 x x x、目标街道宽度 y y y,问这辆车是否能够转弯成功。
分析:将图片按照 y y y 轴翻转,如图建立坐标系。
设车身与 x x x 轴形成的角度为 a a a,则 a a a 的取值范围为 [ 0 , π 2 ] [0, \frac{π}{2}] [0,2π] 。
设题目给的街道宽度分别为 x 1 x_1 x1, y 1 y_1 y1,则我们需要突出关注 ( y 1 , x 1 ) (y_1,x_1) (y1,x1) 这个点。
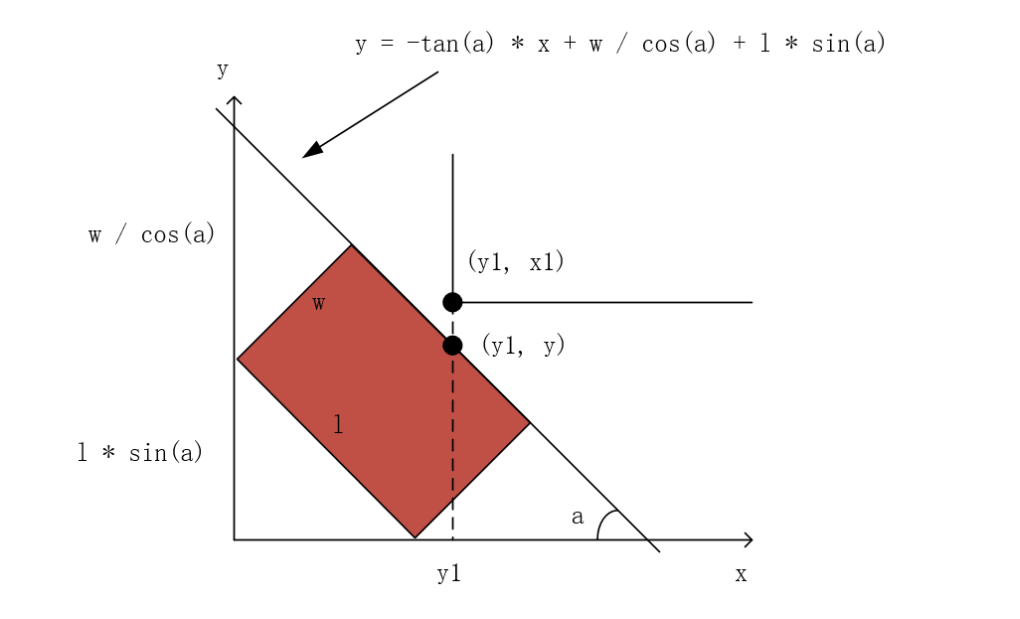
把靠近内侧的车身延长形成直线 y = − t a n ( a ) ∗ x + w c o s ( a ) + l ∗ s i n ( a ) y=-tan(a)*x+\frac{w}{cos(a)}+l*sin(a) y=−tan(a)∗x+cos(a)w+l∗sin(a) 。
我们需要知道在所有 a a a 的取值情况下,在 x = y 1 x = y_1 x=y1 这个点上是否 y > x 1 y>x_1 y>x1 。
现在需要求 a a a 的取值为多少时这条直线才能在 x = y 1 x=y1 x=y1 上得到最大的 y y y 。
易知在车的转弯过程中车身距离内侧墙角的距离先变小后变大,是一个凹函数,因此可以利用三分法求出距离墙角的极小值。(本周是二分练习,三分也是要学习的,还不会的赶紧去百度!)
求出目标角度 a a a 之后在直线方程中代入 x = y 1 x=y_1 x=y1,若 y < = x 1 y<=x_1 y<=x1 则通过,否则不能通过。详见代码。
Code:
const int MAXN = 5010;
const double eps = 1e-5; // 控制精度
const double PI = acos(-1.0); // 小技巧,π的取值
double x, y, l, w;
double f(double a) // 车身直线
{
return -tan(a) * y + w / cos(a) + l * sin(a);
}
double check(double l, double r) // 三分法
{
double lm, rm;
while (r - l > eps)
{
lm = (l + r) / 2;
rm = (lm + r) / 2;
if (f(lm) > f(rm))
{
r = rm;
}
else
{
l = lm;
}
}
return l;
}
int main()
{
while (cin >> x >> y >> l >> w)
{
// 至少要满足两侧街道宽度不少于车的宽度
if (w > x || w > y || f(check(0, PI / 2)) > x)
{
cout << "no" << endl;
}
else
{
cout << "yes" << endl;
}
}
return 0;
}
1006:Cup(数学+二分)
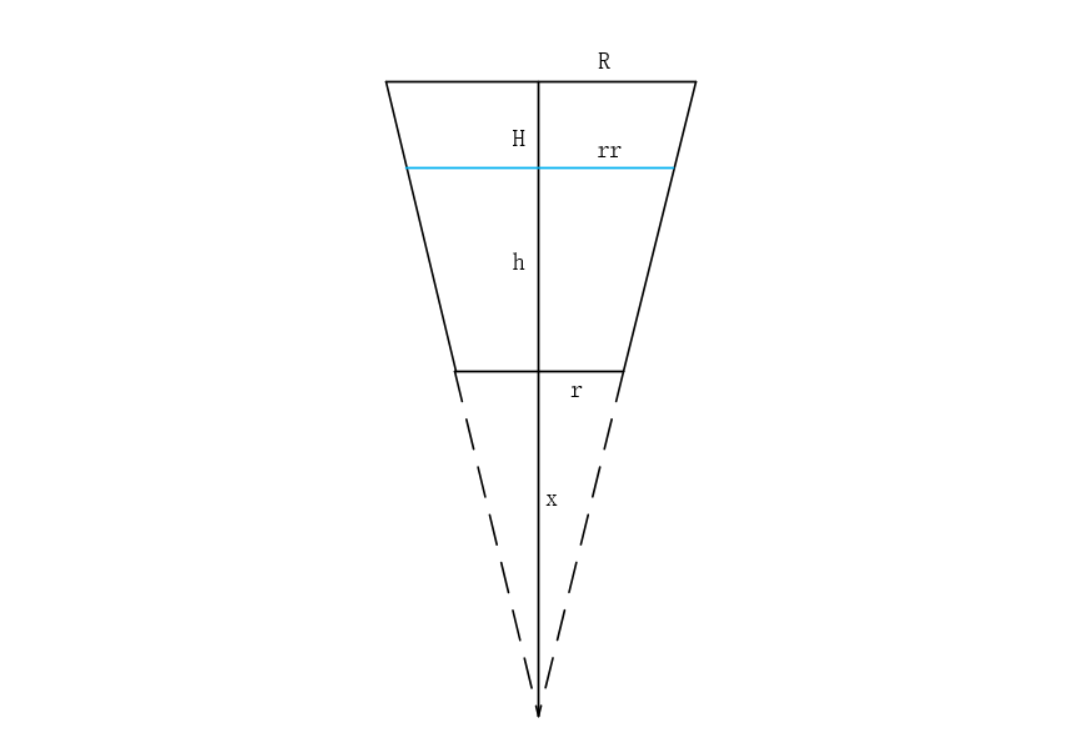
题意:给一个杯子的下圆半径 r r r 、上圆半径 R R R 、高度 H H H 以及杯中水的体积 V V V,求杯中水的高度。
分析:杯子的形状可能是一个圆柱体,也可能是一个圆台,设杯中水的高度为 h h h,水面半径为 r r rr rr 。
① 圆柱体:用体积 V V V 除以底面积 S S S 即可,即 h = V π r 2 h = \frac{V}{πr^2} h=πr2V 。
② 圆台:将圆台补成圆锥,设此时圆锥的高度为 H + x H+x H+x 如图所示,易得 R H + x = r x \frac{R}{H+x}=\frac{r}{x} H+xR=xr,即 x = H r R − r x=\frac{Hr}{R-r} x=R−rHr 。
且 r r h + x = R H + x \frac{rr}{h+x} = \frac{R}{H+x} h+xrr=H+xR,即 r r = R ( h + x ) H + x rr = \frac{R(h+x)}{H+x} rr=H+xR(h+x), 这样只要确定了 h h h 的值那么 r r rr rr 的值也就可以确定了。
又因为圆台体积公式 V = 1 3 π h ( R 2 + r 2 + R ∗ r ) V=\frac{1}{3}πh(R^2+r^2+R*r) V=31πh(R2+r2+R∗r), V V V 随着 h h h 的增大而增大,因此就可以上二分确定水的高度 h h h,检查体积是否为 V V V 。详见代码。
Code:
const double PI = acos(-1.0);
double f(double h, double R, double r) // 圆台体积公式
{
return PI * h * (R * R + r * r + R * r) / 3;
}
int main()
{
int T;
cin >> T;
while (T--)
{
double r, R, H, V;
cin >> r >> R >> H >> V;
if (r == R) // 如果是圆柱体
{
cout << fixed << setprecision(6) << V / (PI * r * r) << endl;
continue;
}
double x = H * r / (R - r); // 得到x
double left = 0, right = H;
while (right - left > eps) // 二分确定答案
{
double mid = (right + left) / 2; // 确定高度
double rr = R * (mid + x) / (H + x); // 确定半径
if (f(mid, rr, r) < V) // 根据体积缩小范围
{
left = mid;
}
else
{
right = mid;
}
}
cout << fixed << setprecision(6) << left << endl;
}
return 0;
}
1008:Can you find it?(合并排序+二分)
题意:给三个数组 A , B , C A,B,C A,B,C,在给一系列的值 X X X,问是否能在三个数组中各取一个值满足 A i + B j + C k = X A_i+B_j+C_k=X Ai+Bj+Ck=X 。
分析: n n n 最大可以是 500 500 500,询问最多有 1000 1000 1000 条。
如果对于每条询问都执行三重循环枚举的话 50 0 3 ∗ 1000 > 1 e 11 500^3*1000>1e11 5003∗1000>1e11 必然超时!
而如果选择事先对数组 C C C 进行排序,之后执行两重循环枚举 A i A_i Ai 和 B j B_j Bj,在 C C C 中二分查找需要的值 X − A i − B j X-A_i-B_j X−Ai−Bj,这样 50 0 2 ∗ l o g 2 ( 500 ) ∗ 1000 > 2 e 9 500^2*log_2(500)*1000 > 2e9 5002∗log2(500)∗1000>2e9,依然会超时!
现在考虑先双重循环枚举 B j , C k B_j,C_k Bj,Ck,将它们的和保存到新数组 D D D 中,并且排序,之后一重循环枚举 A i A_i Ai,然后在 D D D 中二分查询需要的值 X − A i X-A_i X−Ai,这样 500 ∗ l o g 2 ( 500 ∗ 500 ) ) ∗ 1000 < 1 e 7 500*log_2(500*500))*1000 < 1e7 500∗log2(500∗500))∗1000<1e7,这个就不会超时了。
Notice:这题有点莫名其妙,我的数组开小了给我提示 M L E MLE MLE,我把数组再开大就 A C AC AC 了。
Code:
const int MAXN = 500 + 10;
int A[MAXN], B[MAXN], C[MAXN], D[MAXN*MAXN]; // 注意数组D的大小
int main()
{
int L, N, M;
int kase = 1;
while (cin >> L >> N >> M)
{
cout << "Case " << kase++ << ":" << endl;
for (int i = 0; i < L; i++)
{
cin >> A[i];
}
for (int i = 0; i < N; i++)
{
cin >> B[i];
}
for (int i = 0; i < M; i++)
{
cin >> C[i];
}
int index = 0;
for (int i = 0; i < N; i++) // 双重循环处理数组D
{
for (int j = 0; j < M; j++)
{
D[index++] = B[i] + C[j];
}
}
sort(D, D + index); // 必须要排序,二分查找的前提就是有序
int k;
cin >> k;
for (int i = 0; i < k; i++)
{
int target;
cin >> target;
int ok = 0;
for (int j = 0; j < L; j++)
{
int pos = lower_bound(D, D + index, target - A[j]) - D; // 在D中二分查找目标值
if (pos >= index) // 没找到,继续
continue;
if (D[pos] + A[j] == target) // 找到了,输出答案
{
ok = 1;
break;
}
}
if (ok)
cout << "YES" << endl;
else
cout << "NO" << endl;
}
}
return 0;
}
1009:Toxophily(物理/三分+二分)
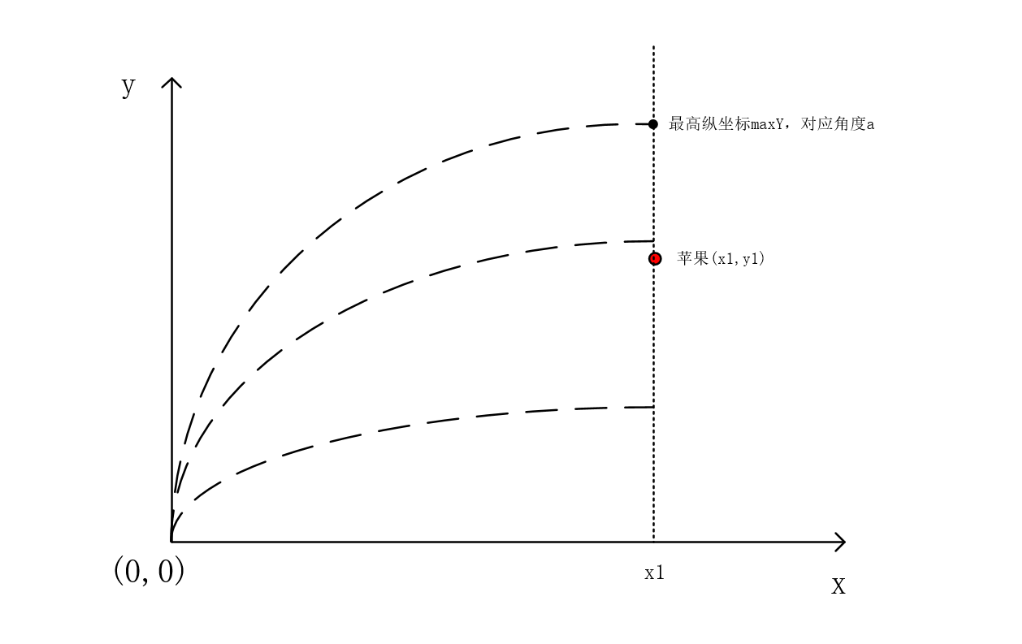
题意:规定人站在起点 x = 0 x = 0 x=0,且人的高度 y = 0 y = 0 y=0 进行射箭,给定箭的初速度 v v v,现在要求最小的角度 a a a,让这支箭能够射到位于 ( x , y ) (x, y) (x,y) 的苹果,箭会受到重力的影响, g = 9.8 N / m g = 9.8N/m g=9.8N/m 。
分析:设苹果的位置为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),我们首先需要知道这支箭在所有的角度下射出去到达 x = x 1 x=x_1 x=x1 时的最大高度 m a x Y maxY maxY 是否满足 m a x Y > = y 1 maxY>=y_1 maxY>=y1 ,只要满足这个条件,那么就一定有解。
根据我们的生活常识,随着角度的变大,落在 x = x 1 x = x_1 x=x1 上的 y y y 值会先增后减,即使一个凸函数,那么我们就可以使用三分来确定极值点对应的角度 a a a,当然也可以使用物理的方式进行分析计算得到 a a a,我这里采取后者。
首先我们假设这支箭是可以射到 x = x 1 x = x_1 x=x1 处的,我们计算在这个角度 a a a 下到达 x 1 x_1 x1 的高度 y y y 。
如果这支箭不能到达 x 1 x_1 x1,那么计算出来的 y y y 值是一个负数,可能不能满足要求。
设箭到达 x 1 x_1 x1 的时间 t = x v cos ( a ) t = \frac{x}{v\cos(a)} t=vcos(a)x,
那么根据匀变速运动公式 y = v t − 1 2 g t 2 = v sin ( a ) ∗ x v cos ( a ) − 1 2 g ∗ x 2 v 2 cos 2 ( a ) = x tan ( a ) − g x 2 2 v 2 cos 2 ( a ) y=vt-\frac{1}{2}gt^2=v\sin(a)*\frac{x}{v\cos(a)}-\frac{1}{2}g*\frac{x^2}{v^2\cos^2(a)}=x\tan(a)-\frac{gx^2}{2v^2\cos^2(a)} y=vt−21gt2=vsin(a)∗vcos(a)x−21g∗v2cos2(a)x2=xtan(a)−2v2cos2(a)gx2
求导 y ′ = x cos 2 ( a ) − g x 2 2 v 2 ∗ 2 sin ( a ) cos 3 ( a ) = x cos 2 ( a ) − g x 2 v 2 ∗ sin ( a ) cos 3 ( a ) y’=\frac{x}{\cos^2(a)}-\frac{gx^2}{2v^2}*\frac{2\sin(a)}{\cos^3(a)}=\frac{x}{\cos^2(a)}-\frac{gx^2}{v^2}*\frac{\sin(a)}{\cos^3(a)} y′=cos2(a)x−2v2gx2∗cos3(a)2sin(a)=cos2(a)x−v2gx2∗cos3(a)sin(a)
令 y ′ = 0 y’=0 y′=0 得 a = arctan ( v 2 g x ) a = \arctan(\frac{v^2}{gx}) a=arctan(gxv2)
这样我们就通过了计算的方式而不是三分得到了目标 a a a 的值。
那么我们就知道了 y = x tan ( a ) − g x 2 2 v 2 cos 2 ( a ) y = x\tan(a)-\frac{gx^2}{2v^2\cos^2(a)} y=xtan(a)−2v2cos2(a)gx2 在 [ 0 , a ] [0,a] [0,a] 的范围中单调递增,因此我们进行二分,查找 y = y 1 y = y_1 y=y1 时对应的角度 a a a 。
Code:
const double eps = 1e-8;
const double g = 9.8;
double x, y, v;
double f(double a) // 角度a下在x=x1时的y
{
return x * tan(a) - g * x * x / (2 * v * v * cos(a) * cos(a));
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> x >> y >> v;
double left = 0, right = atan(v * v / (g * x)); // 计算目标角度a
if (f(right) < y) // 如果最大值还达不到苹果的高度,无解
{
cout << -1 << endl;
continue;
}
left = 0;
while (right - left > eps) // 否则进行二分
{
double mid = (left + right) / 2;
if (f(mid) < y)
{
left = mid;
}
else
{
right = mid;
}
}
cout << fixed << setprecision(6) << right << endl;
}
return 0;
}
1010:Pie(二分答案)
题意:给 n n n 个圆的半径,现在需要在这些圆中割出大小相同的 f f f 个小圆,问小圆的最大 s i z e size size 。
分析:典型的二分答案,我们先二分确定小圆的 s i z e size size,之后贪心得在这 n n n 个圆中割出小圆,检查这样割出的小圆数量是否 > f >f >f 。
Notice:这题精度有点毒瘤,直接二分半径可能不够,应该要二分半径的平方,因为算出半径之后还需要算 s i z e = π r 2 size = πr^2 size=πr2,因此可以对 r 2 r^2 r2 进行二分。除此以外还要注意在 c h e c k check check 的时候要向下取整!
Code:
const int MAXN = 1e4 + 10;
const double eps = 1e-6;
const double PI = acos(-1.0);
int n, f;
double arr[MAXN];
int check(double mid) // 贪心检查是否满足要求
{
int cnt = 0;
for (int i = 0; i < n; i++)
{
cnt += (int)(arr[i] / mid); // 注意向下取整
}
return cnt >= f;
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> n >> f;
f++;
double maxV = 0;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
arr[i] = arr[i] * arr[i]; // 先变成r^2
maxV = max(maxV, arr[i]); // 确定右边界
}
double l = 0, r = maxV;
double mid;
while (r - l > eps) // 二分确定最大r^2
{
mid = (r + l) / 2;
if (check(mid))
{
l = mid;
}
else
{
r = mid;
}
}
cout << fixed << setprecision(4) << mid * PI << endl; // 输出πr^2
}
return 0;
}
1012:Shell Pyramid(数学+二分)
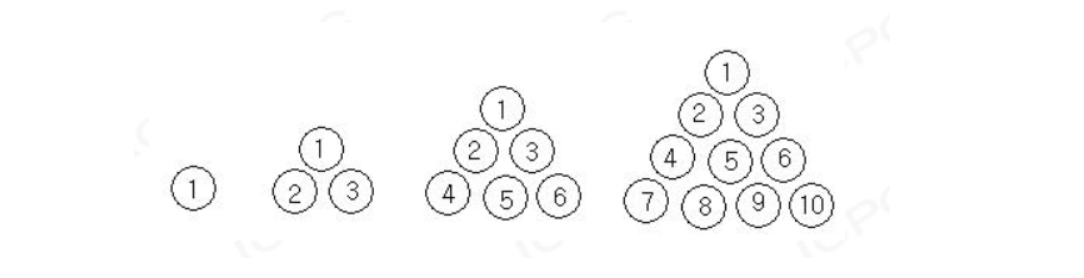
题意:有一个金字塔,如下图从左到右代表金字塔从上到下的横截面,第一层 1 1 1 个,第二层比第一层多 2 2 2 个,第三层比第二层多 3 3 3 个 … 以此类推。现在要求整个金字塔中第 n n n 个所在的层数、行数以及列数。例如第 4 4 4 个是在第 2 2 2 层第 2 2 2 行第 2 2 2 个,第 19 19 19 个是在第 4 4 4 层第第 4 4 4 行第 3 3 3 个。
分析:我们可以先确定第 n n n 个是在第几层。
设 A [ i ] A[i] A[i] 表示前 i i i 层的元素数量,那么 A [ 1 ] = 1 , A [ 2 ] = 4 , A [ 3 ] = 10… A[1] = 1, A[2] = 4, A[3] = 10 … A[1]=1,A[2]=4,A[3]=10...
那么 A [ i ] A[i] A[i] 满足的典型的三角形金字塔数 A [ n ] = C n + 2 3 = n ( n + 1 ) ( n + 2 ) 6 A[n] = C_{n+2}^3=\frac{n(n+1)(n+2)}{6} A[n]=Cn+23=6n(n+1)(n+2)
因为数据最大为 s = 2 63 s = 2^{63} s=263,那么 A [ i ] A[i] A[i] 值需要到 i = 1 e 6 i = 1e6 i=1e6 就可以了,因此我们可以先预处理出这个数组 A A A,然后进行二分找到第一个大于等于 s s s 的 A [ i ] A[i] A[i],这样就得到了对应的层数 i i i 。
那么接下来我们只需要知道 s − A [ i − 1 ] s-A[i-1] s−A[i−1] 在当前层的哪一行就可以知道对应的列。
设 B [ j ] B[j] B[j] 表示第 i i i 层的元素数量,那么 B [ 1 ] = 1 , B [ 2 ] = 3 , B [ 3 ] = 6… B[1] = 1, B[2] = 3, B[3] = 6… B[1]=1,B[2]=3,B[3]=6...
那么 B [ j ] B[j] B[j] 其实就是等差数列,满足 B [ n ] = n ( n + 1 ) 2 B[n] = \frac{n(n+1)}{2} B[n]=2n(n+1)
同样我们预处理前 1 e 6 1e6 1e6 层的 B B B 数组,二分找到第一个大于等于 s − A [ i − 1 ] s-A[i-1] s−A[i−1] 的 B [ j ] B[j] B[j],这样就得到了对应的行数 j j j,那么得到对应的列数 s − A [ i − 1 ] − B [ j − 1 ] s-A[i-1]-B[j-1] s−A[i−1]−B[j−1] 。详见代码。
Code:
const int MAXN = 1e6 + 10;
int num[MAXN], sum[MAXN]; // 分别代表数组B和A
int main()
{
for (int i = 1; i < MAXN; i++) // 预处理B数组
{
num[i] = num[i - 1] + i;
}
for (int i = 1; i < MAXN; i++) // 预处理A数组
{
sum[i] = sum[i - 1] + num[i];
}
int T;
cin >> T;
while (T--)
{
int s;
cin >> s;
int pos1 = lower_bound(sum, sum + MAXN, s) - sum; // 调库二分找到对应的层数
s -= sum[pos1 - 1];
int pos2 = lower_bound(num, num + MAXN, s) - num; // 调库二分找到对应的行数
s -= num[pos2 - 1];
cout << pos1 << " " << pos2 << " " << s << endl; // 输出层、行、列
}
return 0;
}
1013:Cable master(二分答案)
题意:给 n n n 根电缆的长度,需要切割出长度相等的 k k k 根电缆,问最大的长度。
分析:与 1010 1010 1010 类似,二分答案,然后贪心地检查就可以了。详见代码。
Code:
// 在[0, maxV]中二分切割的长度x,遍历n条现有的电缆,电缆长度/x = 最多可以切割的数量,将数量加起来判断是否 >= k
const int MAXN = 1e4 + 10;
const double eps = 1e-9;
int n, k;
double arr[MAXN];
int check(double mid)
{
int cnt = 0;
for (int i = 0; i < n; i++)
{
cnt += (int)(arr[i] / mid); // 注意向下取整
}
return cnt >= k;
}
int main()
{
while (cin >> n >> k, n + k)
{
double l = 0, r = 0;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
r = max(r, arr[i]); // 确定右边界
}
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid))
{
l = mid;
}
else
{
r = mid;
}
}
cout << fixed << setprecision(2) << l << endl;
}
return 0;
}
1016:Assemble(二分答案+分桶优化)
题意:需要组装电脑,现在给 n n n 个配件的信息以及预算 b b b,给的配件中会出现类型相同的不同型号配件,需要在所有类型的配件中选择其中一件来组装电脑,而电脑的性能满足木桶短板效应,取决于其中质量最差的配件。现在要问不超出预算的情况下组装的电脑能得到的最大性能。
分析:也是典型的二分答案,我们先二分确定电脑的性能,之后贪心的在所有的配件中进行选择,选择的配件质量不能小于当前二分的答案,如果最后选择了所有需要的配件并且没有超出预算就算满足要求。
如果直接这么写的话就 T L E TLE TLE 了。。。我们考虑优化,不需要在每次检查的时候对 n n n 个配件都进行检查,可以先把同类的配件按照价格升序放在一起,这样我们检查答案的时候就可以在每一类配件中选择最便宜的满足答案的配件后及时退出,继续到下一类中进行寻找!详见代码。
Code:
const int MAXN = 1000 + 10;
int n, money, cnt;
struct Good // 货物
{
string type, name; // 类别,名称
int price, quality; // 价格,质量
bool operator<(Good other) const // 自定义排序规则
{
return price < other.price; // 注意是按照价格排序
}
} goods[MAXN];
map<string, int> id; // 为每一类配件分配索引
vector<Good> vec[MAXN]; // 有很多个桶,里面保存同类货物
int check(int mid) // 检查答案
{
int cost = 0; // 保存费用
for (int i = 0; i < cnt; i++) // 遍历所有类别的配件
{
int ok = 0; // 用来确定是否成功选择了配件
for (auto v : vec[i]) // 枚举每个类别中的配件,C++11中的用法,用普通的for循环也一样
{
if (v.quality >= mid) // 因为已经按照价格排序,如果质量达到要求就选择,保证最优性
{
cost += v.price; // 记下已经花的钱
ok = 1; // 成功选择
break;
}
}
if (!ok || cost > money) // 如果没有成功选上或者超出预算了就说明这个答案不可行
return 0;
}
return 1; // 所有类别配件都选择了并且没有超出预算,答案可行
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> n >> money;
id.clear(); // 需要清空map
for (int i = 0; i < n; i++)
vec[i].clear(); // 清空所有的桶
cnt = 0; // 用于分配索引
int l = 0, r = 0;
for (int i = 0; i < n; i++)
{
cin >> goods[i].type >> goods[i].name >> goods[i].price >> goods[i].quality;
r = max(r, goods[i].quality); // 确定右边界
if (!id.count(goods[i].type)) // 这个类别的配件没有出现过则分配新的索引
{
id[goods[i].type] = cnt++;
}
vec[id[goods[i].type]].push_back(goods[i]); // 把这个配件放到同类的桶中
}
for (int i = 0; i < cnt; i++) // 对所有的桶按照价格从低到高进行排序
{
sort(vec[i].begin(), vec[i].end());
}
while (r > l) // 二分确定答案
{
int mid = (l + r + 1) / 2;
if (check(mid))
{
l = mid;
}
else
{
r = mid - 1;
}
}
cout << l << endl;
}
return 0;
}
三、hard
1001:Fibonacci Numbers(通项公式+矩阵快速幂)
题意:求斐波那契数列第 n n n 项的值, n ∈ [ 0 , 1 e 8 ] n\in[0, 1e8] n∈[0,1e8],由于 n n n 非常大,最多只需要输出 8 8 8 位的答案,如果超过了 8 8 8 位则输出前 4 4 4 位以及后 4 4 4 位,中间加上 “…”。
分析:我吐了,又是数学题,需要用到斐波那契的通项公式 f n = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] f_n = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n] fn=51[(21+5)n−(21−5)n] 以及矩阵快速幂。
① n < 40 n < 40 n<40 时,该数列的位数不超过 8 8 8 位,因此这个部分直接预处理打表就可以了。
② n > = 40 n >= 40 n>=40,分成高四位与低四位。
低四位可以用矩阵快速幂计算:
f n = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] f_n = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n] fn=51[(21+5)n−(21−5)n] ( n > = 1 ) (n >= 1) (n>=1)
( f n f n − 1 ) = ( 1 1 1 0 ) n − 1 ( f 1 f 0 ) \begin{pmatrix} f_n \\f_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\1 & 0 \end{pmatrix}^{n-1}\begin{pmatrix} f_1\\f_0\end{pmatrix} (fnfn−1)=(1110)n−1(f1f0) ( n > = 1 ) (n >= 1) (n>=1)
然后直接套上矩阵快速幂就可以啦。
高四位需要用到斐波那契的通项公式:
此时 f n = 1 5 ( 1 + 5 2 ) n f_n = \frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^n fn=51(21+5)n ,因为此时 − ( 1 − 5 2 ) n -(\frac{1-\sqrt{5}}{2})^n −(21−5)n 的影响已经非常小可以忽略不计了。由于我们只需要前四位,所以进行如下处理:
设 l e n len len 为 s s s 的长度
我们知道 s = d . x x x × 1 0 l e n − 4 s = d.xxx\times10^{len-4} s=d.xxx×10len−4,例如 123456 = 1234.56 × 1 0 2 123456=1234.56\times10^2 123456=1234.56×102
得到 l o g 10 ( s ) = l o g 10 ( d . x x x ) + l e n − 4 log_{10}(s)=log_{10}(d.xxx)+len-4 log10(s)=log10(d.xxx)+len−4, l o g 10 ( 123456 ) = l o g 10 ( 1234.56 ) + 2 log_{10}(123456)=log_{10}(1234.56)+2 log10(123456)=log10(1234.56)+2
那么 d . x x x = 1 0 l o g 10 ( s ) − l e n + 4 d.xxx=10^{log_{10}(s)-len+4} d.xxx=10log10(s)−len+4, 1234.56 = 1 0 l o g 10 ( 123456 ) − 2 1234.56=10^{log_{10}(123456)-2} 1234.56=10log10(123456)−2
而 d d d 就是我们需要求的前四位,只需要把 d . x x x d.xxx d.xxx 的小数部分去除就可以了。
( l e n = ( i n t ) l o g 10 ( s ) + 1 len = (int)log_{10}(s)+1 len=(int)log10(s)+1)
对于这道题, s = 1 5 ( 1 + 5 2 ) n s=\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^n s=51(21+5)n,则 l o g 10 ( s ) = l o g 10 ( 1 5 ) + n ∗ l o g 10 ( 1 + 5 2 ) log_{10}(s)=log_{10}(\frac{1}{\sqrt{5}})+n*log_{10}(\frac{1+\sqrt{5}}{2}) log10(s)=log10(51)+n∗log10(21+5),详见代码。
参考:
https://www.cnblogs.com/martinue/p/5490535.html
https://www.cnblogs.com/heyujun/p/10298953.html
Code:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 40 + 10; // 只需要打表前40项就足够了
const int Mod = 1e4; // 在进行快速幂的时候用到,保留后四位
int N;
struct Matrix // 矩阵
{
int m[2][2];
Matrix() {
memset(m, 0, sizeof(m)); }
void init() // 初始化
{
for (int i = 0; i < 2; i++)
m[i][i] = 1;
}
int *operator[](int id) {
return m[id]; }
Matrix operator*(const Matrix &b) // 矩阵乘法
{
Matrix res;
for (int i = 0; i < 2; i++)
for (int j = 0; j < 2; j++)
for (int k = 0; k < 2; k++)
res[i][j] = (res[i][j] + m[i][k] * b.m[k][j] % Mod) % Mod;
return res;
}
};
int fibo[MAXN]; // 保存斐波那契打表的结果
int solve1() // 处理前四位
{
double s = log10(sqrt(5.0) / 5.0) + 1.0 * N * log10((1.0 + sqrt(5.0)) / 2.0); // 这里直接把s变成log(s)
s = s - (int)s; // 这一步和下一步一起相当于 10^(log(s)-len+4)
double ans = 1000 * pow(10.0, s);
return ans;
}
int solve2() // 处理后四位,矩阵快速幂
{
Matrix S, T, ans;
int n = N;
ans.init();
S[0][0] = 1;
T[0][0] = 1, T[0][1] = 1;
T[1][0] = 1, T[1][1] = 0;
while (n)
{
if (n & 1)
ans = ans * T;
n >>= 1;
T = T * T;
}
S = ans * S;
return ans[1][0];
}
int main()
{
fibo[0] = 0, fibo[1] = 1; // 打出前40的表
for (int i = 2; i <= 40; i++)
fibo[i] = fibo[i - 1] + fibo[i - 2];
while (~scanf("%d", &N))
{
if (N < 40) // 如果是前40项直接输出
printf("%d\n", fibo[N]);
else // 否则处理前四位和后四位
{
printf("%04d...%04d\n", solve1(), solve2());
}
}
return 0;
}
1011:Line belt(三分套三分)
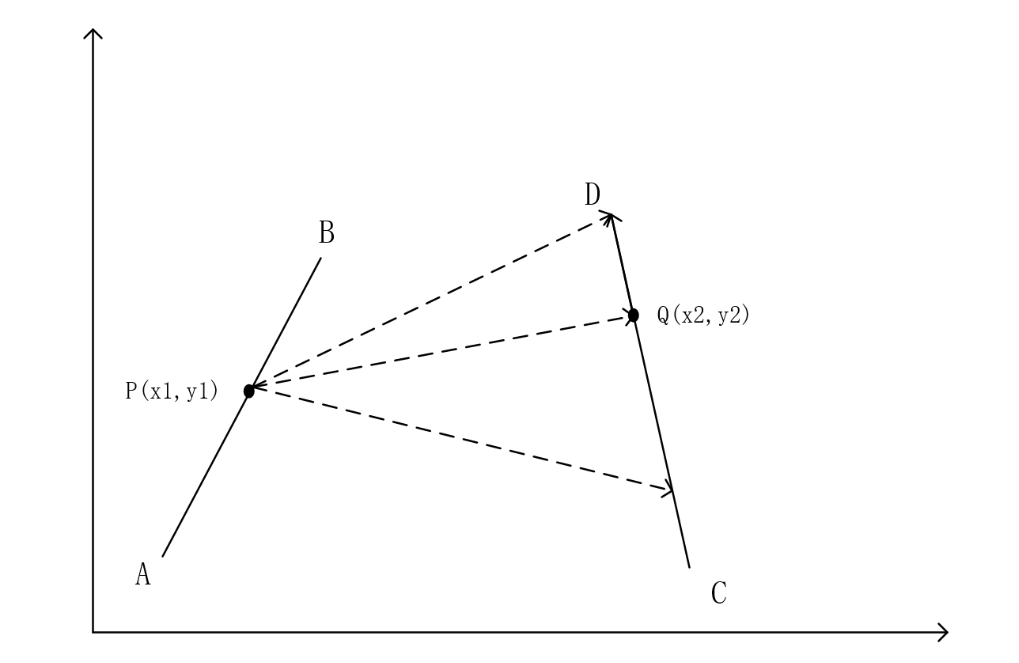
题意:给两条线段 A B AB AB 以及 C D CD CD,在线段 A B AB AB 上的速度为 P P P,在线段 C D CD CD 上的速度为 Q Q Q,在其他区域的速度为 R R R 。现在要从 A A A 到 D D D,求最短时间。
分析:因为需要从 A A A 走到 D D D,那么一定是从 A B AB AB 上离开,从 C D CD CD 上进行,那么我们设离开点为 P ( x 1 , y 1 ) P(x_1,y_1) P(x1,y1),进入点为 Q ( x 2 , y 2 ) Q(x_2, y_2) Q(x2,y2) 。
那么如何确定这两个点呢?先简化一下问题,假若给定了 P P P,那么怎么确定 Q Q Q 呢?
如图,因为 C D CD CD 上的速度与空白区域的速度是不同的,因此:
若空白区域的速度 R R R 大于 C D CD CD 上的速度 Q Q Q,那么从 P P P 直接到 D D D 即可;
否则先到 C D CD CD 的中部 Q Q Q 点再到 D D D 点。
不论哪种情况,随着 Q Q Q 点从 C C C 到 D D D 的移动过程中, P P P 到 D D D 的时间先减后增,或者单调递减,三分都可以应付,因此如果确定了 P P P 点,我们就可以使用三分法来求得 P P P 到 D D D 的最短时间。
那么现在的问题就是如何确定点 P P P 呢?
类似于刚刚的分析,随着 P P P 点从 A A A 到 B B B 移动过程中, A A A 到 D D D 的时间先减后增,或者单调递增,因此我们还是可以使用三分法来确定 P P P 点,这样一来,我们需要求的 P P P 和 Q Q Q 都求出来了,计算答案即可。
Notice:可以学习一下用结构体 P o i n t Point Point 来进行二分的方法。
Code:
const double eps = 1e-9;
struct Point // 点
{
double x, y; // 横纵坐标
Point(double _x, double _y) // 构造函数,初始化
{
x = _x;
y = _y;
}
};
double distance(Point x, Point y) // 求出两点之间的距离
{
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
double ax, ay, bx, by, cx, cy, dx, dy, p, q, r; // ABCD的坐标以及各个位置的速度
double f(Point a, Point b) // 确定P和Q点之后求从P到D的时间
{
double t = distance(a, b) / r + distance(a, Point(dx, dy)) / q;
return t;
}
double calc(Point a) // 确定P点之后求从P到D的时间
{
Point l(cx, cy), r(dx, dy);
while (distance(l, r) > eps) // 三分计算
{
Point lm((r.x + l.x) / 2, (r.y + l.y) / 2);
Point rm((lm.x + r.x) / 2, (lm.y + r.y) / 2);
if (f(lm, a) < f(rm, a)) // 凹函数,舍弃右边
{
r = rm;
}
else
{
l = lm;
}
}
return f(l, a) + distance(Point(ax, ay), a) / p; // P到D的时间+A到P的时间
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> ax >> ay >> bx >> by >> cx >> cy >> dx >> dy;
cin >> p >> q >> r;
Point l(ax, ay), r(bx, by);
while (distance(l, r) > eps) // 三分计算
{
Point lm((r.x + l.x) / 2, (r.y + l.y) / 2); // 学习一下,结构体来二分
Point rm((lm.x + r.x) / 2, (lm.y + r.y) / 2);
if (calc(lm) < calc(rm)) // 凹函数,舍弃右边
{
r = rm;
}
else
{
l = lm;
}
}
cout << fixed << setprecision(2) << calc(l) << endl;
}
return 0;
}
1018:考研路茫茫——早起看书(三分)
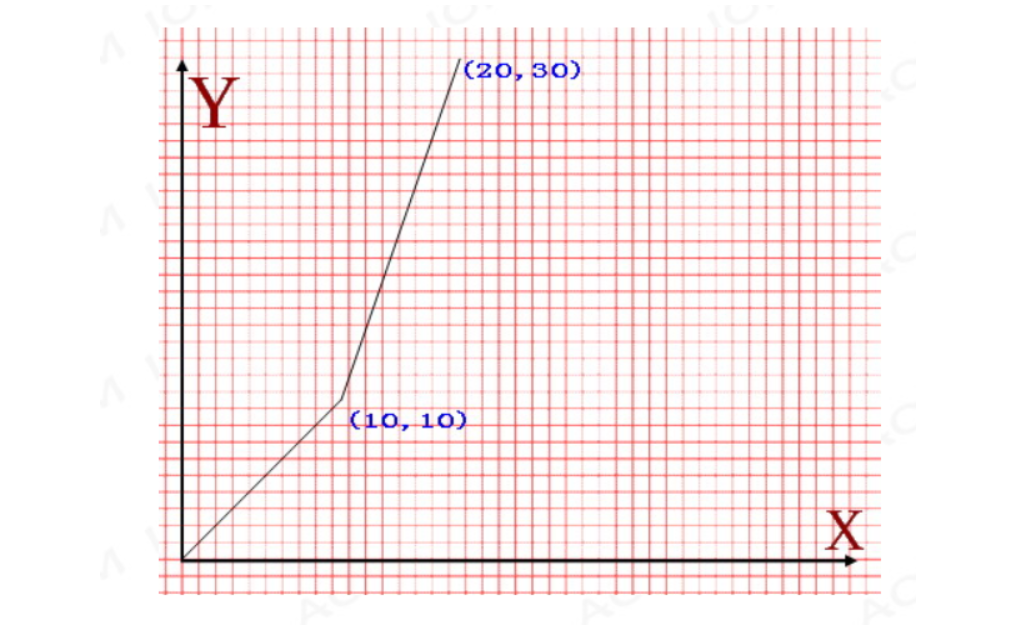
题意:给定 F = N x 2 F = \frac{N}{x^2} F=x2N 以及包含 M M M 个点的折线图 Y Y Y,保证 Y Y Y 是不降的,现在问最小的 ( F + Y ) (F+Y) (F+Y) 的值是多少。
分析:我们首先需要明确最小 ( F + Y ) (F+Y) (F+Y) 对应的横坐标 x x x 可能是在折线图 Y Y Y 两点之间的,而两点 i , ( i − 1 ) i,(i-1) i,(i−1) 之间的连线方程为 y i = k ∗ ( x i − x i − 1 ) + y i − 1 y_i = k*(x_i-x_{i-1})+y_{i-1} yi=k∗(xi−xi−1)+yi−1, k k k 为斜率。
设 Q = ( F + Y ) = N x 2 + k ∗ ( x − x i − 1 ) + y i − 1 Q = (F+Y) = \frac{N}{x^2}+k*(x-x_{i-1})+y_{i-1} Q=(F+Y)=x2N+k∗(x−xi−1)+yi−1,
则 Q ′ = − 2 N x 3 + k Q’ = \frac{-2N}{x^3}+k Q′=x3−2N+k,那么我们知道 Q Q Q 可能是单调递减或者先减后增的,可以用三分来求得 i , ( i − 1 ) i,(i-1) i,(i−1) 两点线段中的极小值。
但是因为每段线段的斜率是不同的, 所以我们需要求所有的线段都求出斜率 k k k 再分别进行三分求极小值更新答案。详见代码。
Notice:这题好像精度有点问题…我最后输出三分 l m lm lm 对应的值就对了。
Code:
const int MAXN = 1e4 + 10;
const double eps = 1e-9;
int m, n;
struct Point // 点
{
double x, y; // 横纵坐标
} points[MAXN];
double f(double a, double k, int i) // 求Q
{
return n / (a * a) + k * (a - points[i - 1].x) + points[i - 1].y;
}
int main()
{
while (cin >> m >> n)
{
for (int i = 0; i < m; i++)
{
cin >> points[i].x >> points[i].y;
}
double ans = 1e18; // 这里需要设置一个很大的值
for (int i = 1; i < m; i++) // 枚举每条线段
{
double k = (points[i].y - points[i - 1].y) / (points[i].x - points[i - 1].x); // 求出斜率k
double l = points[i - 1].x, r = points[i].x;
double lm, rm;
while (r - l > eps) // 二分求出线段中的极小值
{
lm = (l + r) / 2;
rm = (lm + r) / 2;
if (f(lm, k, i) < f(rm, k, i))
{
r = rm;
}
else
{
l = lm;
}
}
ans = min(ans, f(lm, k, i)); // 更新答案
}
cout << fixed << setprecision(3) << ans << endl;
}
return 0;
}
四、乱入的二分图
1003:Girls and Boys(二分图最大点独立集)
题意:有一堆的男男女女,现在给出每个人的若干暧昧对象,问最多能抓出多少个互相没有暧昧关系的人。
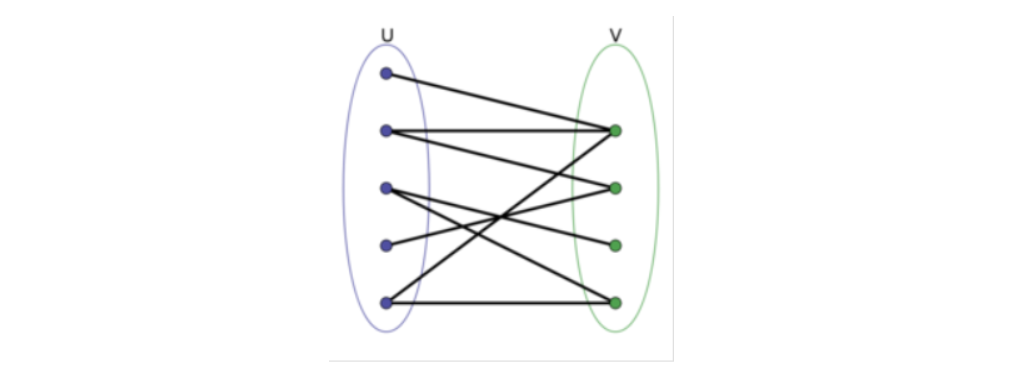
分析: 典型的二分图背景,不过这道题考的是二分图最大点独立集,即其中任意一对点之间没有连线的最大集合。这里有挺多图论的概念,还是等以后图论的时候再细说。这里提一下二分图的概念,在无向图中如果可以把所有的点分成两个不相交的集合,并且图中所有边的两个端点分别位于这两个集合中,这么这个图就成为二分图,如图所示。
图片引用自百度百科——“二分图”
说到二分图就不得不提到最大匹配,常用的算法有匈牙利、网络流Dinic等,初学者只要会用匈牙利算法就可以了,不会的自行百度学习即可。
最大匹配,就是图中的最大边集,满足任意两条边都没有公共的顶点。每个点最多只有一个匹配点。
而对于最大点独立集,现在我们只需要知道一个性质,在二分图中最大点独立集 = n – 最大匹配。
因此我们只需要套上匈牙利模板然后用点的总数 n n n 减去最大匹配就可以了。
Notice:注意要使用邻接表实现的匈牙利模板,邻接矩阵实现的匈牙利在本题会超时!
Code:
const int MAXN = 5010; // 点数的最大值
const int MAXM = 50010; // 边数的最大值
int n;
struct Edge // 边
{
int to, next; // to为边指向的点,next为下一条边
} edge[MAXM];
int head[MAXN], tot; // head为邻接表头,每个head对应一个点,tot表示head的总数
void init() // 初始化
{
tot = 0;
memset(head, -1, sizeof(head));
return;
}
void addEdge(int u, int v) // 加边
{
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
return;
}
int linker[MAXN]; // 保存匹配到的点
bool used[MAXN]; // 记录点是否被使用
int uN; // 记录点的数量
bool dfs(int u) // 寻找增广路
{
for (int i = head[u]; i != -1; i = edge[i].next)
{
int v = edge[i].to;
if (!used[v])
{
used[v] = true;
if (linker[v] == -1 || dfs(linker[v]))
{
linker[v] = u;
return true;
}
}
}
return false;
}
int hungary() // 匈牙利算法
{
int res = 0;
memset(linker, -1, sizeof(linker));
for (int u = 0; u < uN; u++) // 点的编号0~uN-1
{
memset(used, false, sizeof(used));
if (dfs(u))
{
res++;
}
}
return res;
}
int main()
{
while (scanf("%d", &n) == 1)
{
init(); // 多case,注意初始化
uN = n;
for (int i = 0; i < n; i++)
{
int num;
scanf("%d: (%d)", &i, &num); // 使用scanf好格式化输入
for (int j = 0; j < num; j++)
{
int v;
scanf("%d", &v);
addEdge(i, v);
}
}
printf("%d\n", n - hungary() / 2); // 因为这里是同一个集合内部进行匹配,所有匹配数量会乘以2,我们手动除以2
}
return 0;
}
【END】感谢观看!
今天的文章WHUT第五周训练整理分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/63591.html