数字信号处理实验(一)

实验目的

本次实验目的为：在matlab环境下产生几种基本的数字信号，并对这些基本的信号进行运算和变换，同时利用程序结果对采样定理进行验证，深刻理解采样定理。通过自己录制音频信号并对不同的音频信号进行不同处理，加深理解音频信号中声道的原理，以及混声、回声的形成原理。

实验内容

1. 用matlab产生单位脉冲信号，单位阶跃信号，矩形信号，正弦信号，余弦信号，指数信号，产生并观察f(x)=sinc(x)函数的波形。
2. 利用matlab实现离散时间信号的代数运算，移位运算，翻折运算，卷积运算，差分变换和比例变换。
3. 采样定理的验证
   探究采样对信号重构的影响，截频对信号重构的影响。
4. 音频实验

实验结果分析

1. 用matlab产生单位脉冲信号，单位阶跃信号，矩形信号，正弦信号，余弦信号，指数信号，产生并观察f(x)=sinc(x)函数的波形。

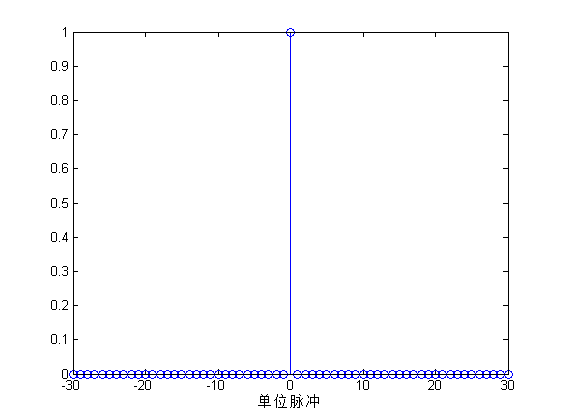
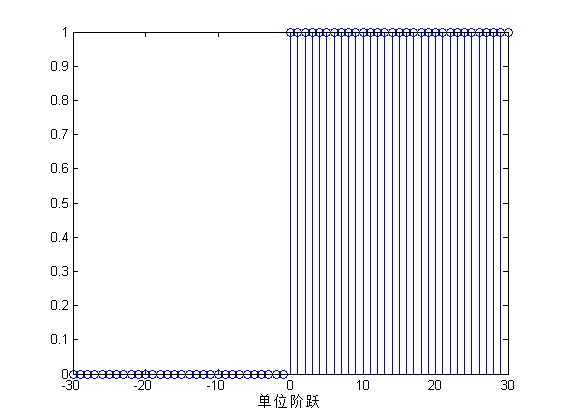
图(a)表示的是单位脉冲序列，图(b)表示的是单位阶跃序列，单位脉冲序列在0处的值为1，在其他点处的值都为0；单位阶跃序列在大于或等于0的点处值为1，其他点处的值都为0。

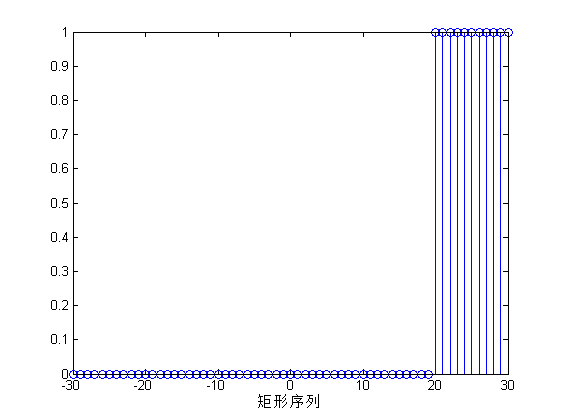
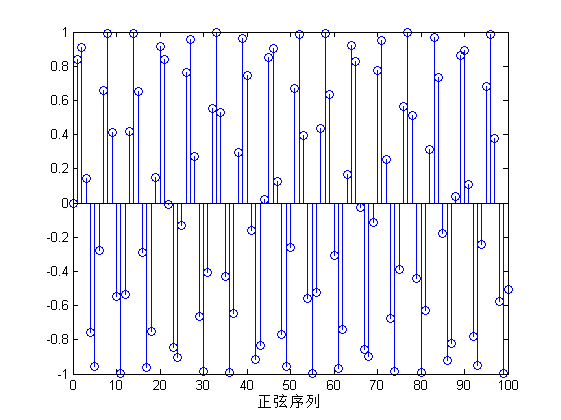
图(c)表示矩形序列，矩形序列在20-30之间的取值为1，其他点取值为0；图(d)表示正弦序列，正弦序列是有明显的周期性。


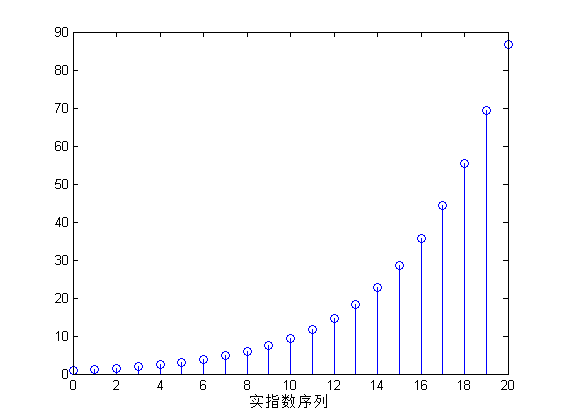
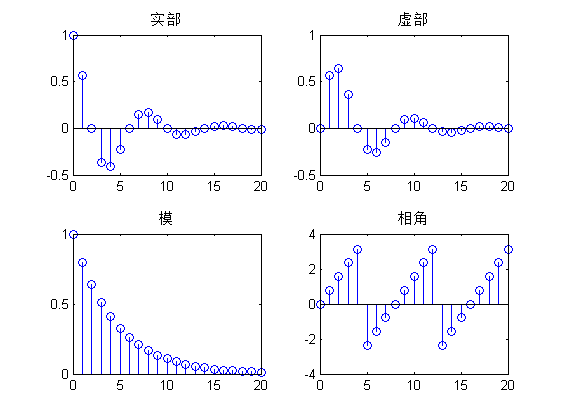
图(e)表示的是实指数序列，其函数原型是 $f(x)=(5/4)^x$图(f)表示的是复指数序列，其中四个子图分别表示复指数序列的实部序列、虚部序列、模值序列和相角序列。其函数原型是 $f(x)=(0.8e^{\pi i/4})^x$。

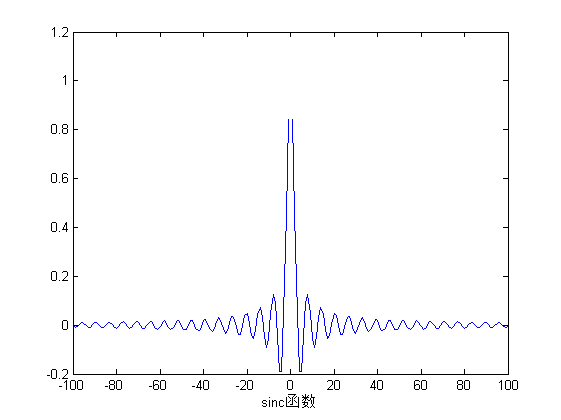
图(g)表示的是sinc函数，sinc函数的原型是$f(x)=sin(x)/x$，数学分析中，经过对sin(x)在0处泰勒展开，可以得到sinc函数在0处的值为1。

2. 利用matlab实现离散时间信号的代数运算，移位运算，翻折运算，卷积运算，差分变换和比例变换。

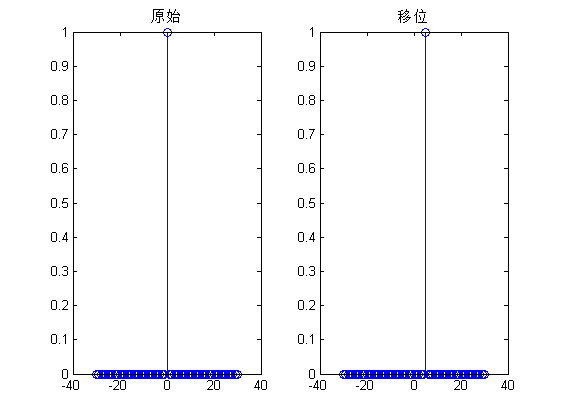
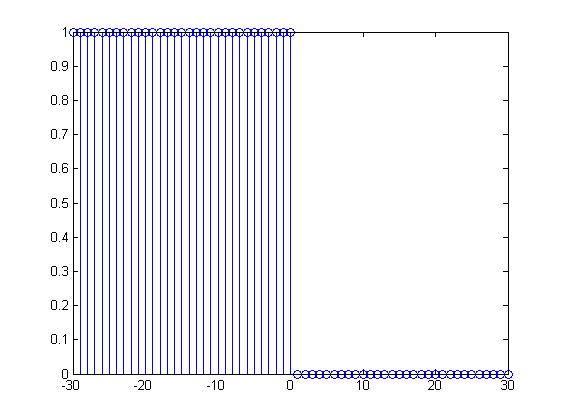
图(a)表示的是单位脉冲序列的移位，左子图是原始序列，右子图是向右移位5个单位的序列。图(b)是单位阶跃序列翻折后的序列。从负无穷到0的值是1，其他点的值都为0。


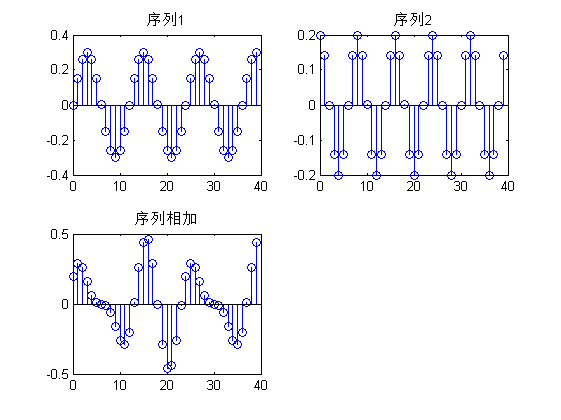
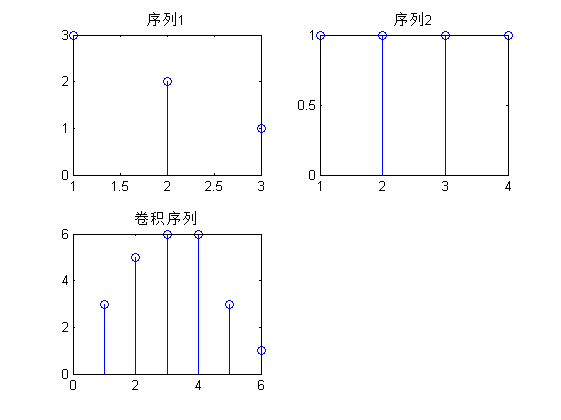
图(c)表示序列1和序列2相加后的效果图，序列1是正弦序列，序列的函数原型是$f(x)=0.3sin(\pi x/6)$；序列2是余弦序列，序列的函数原型是$f(x)=0.2cos(\pi x/4)$ ，图(d)表示序列卷积。

3. 采样定理的验证

探究采样对信号重构的影响，截频对信号重构的影响。
首先对信号采取不同频率的采样，临界采样是奈奎斯特临界值，实验中分别对过采样，欠采样和临界采样三种情形进行了实验，实验结果如下图。


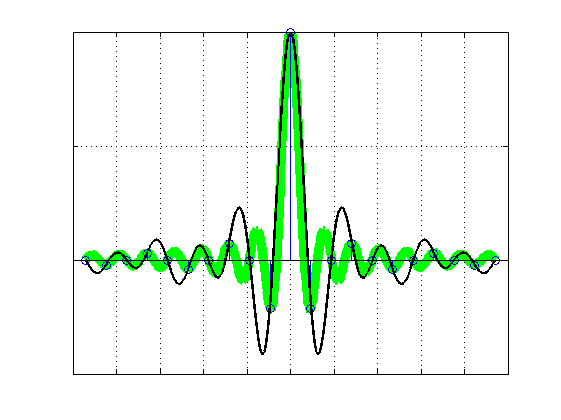
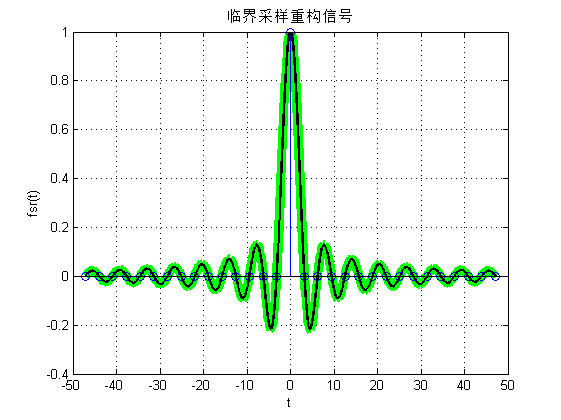
图(a)表示欠采样的情况，图(b)表示临界采样，绿色粗线表示原始信号，黑色细线表示采样后重构的信号，从欠采样和临界采样的实验结果中我们观察到：欠采样重构后的信号和原始信号有一定的差别，而临界采样重构后信号和原始信号近似相同。


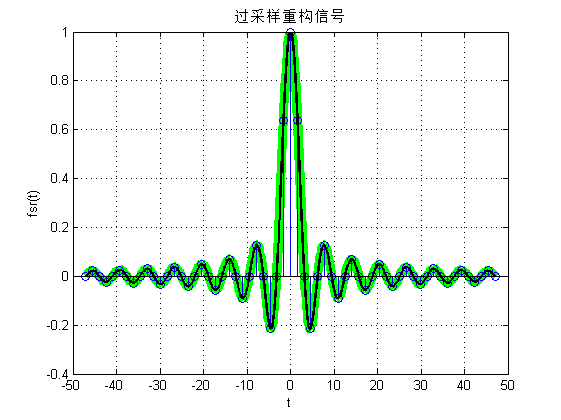
图(c)表示的是过采样情况，图(d)表示的是临界采样情况，绿色粗线表示原始信号，黑色细线表示采样后重构的信号。从两种采样实验结果中可以看出：两种采样后重构后的信号都和原始信号近似相同。
通过此次试验，我们对采样定理有了更深的认识。采样频率必须大于二倍信号谱的最高频率。
下面我们对解频对采样的影响进行分析。实验信号是$f(t)=1(-1\leq t \leq 1)$ 实验信号频谱是$F(w)=2sin(w)/w$


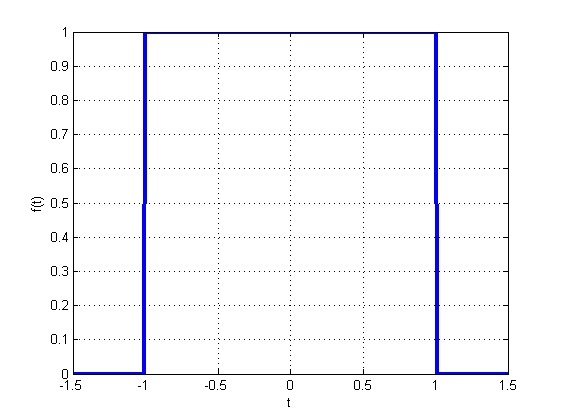
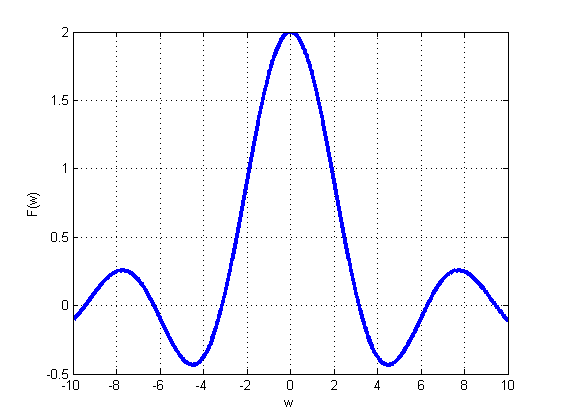
图(a)是原始信号，图(b)是信号的频谱。


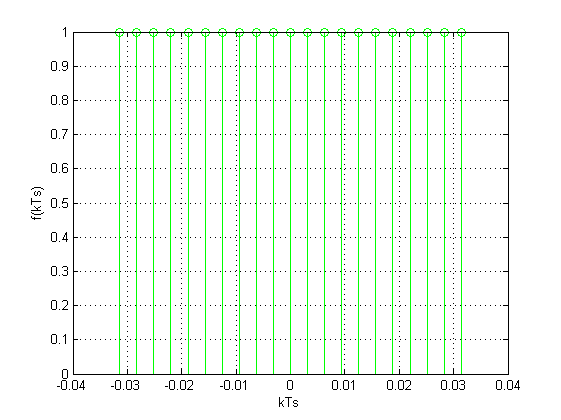
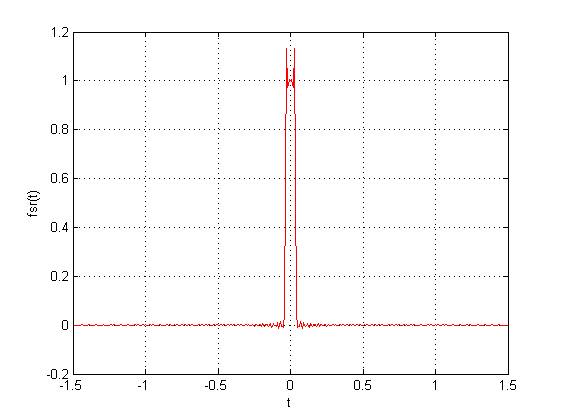
图(c)表示采样截频ws = 1000时的采样信号序列，图(d)是ws = 1000 时的重构后的信号，可以看出当ws的值取1000时，采样过程只能近似取到0附近的信号。


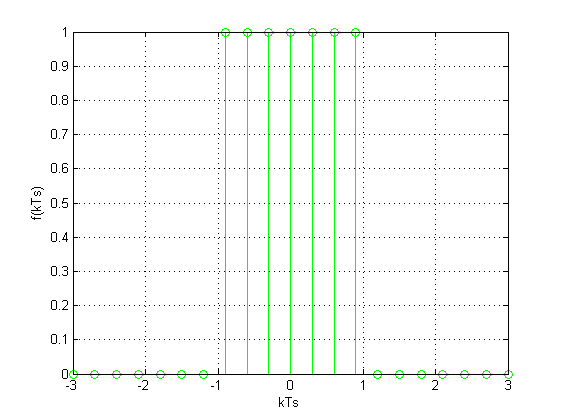
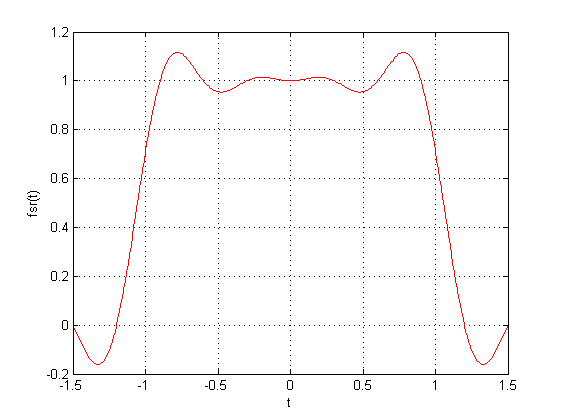
图(e)和图(f) 是截止频率为 时的采样序列和重构信号，可以看出此时要比ws = 1000 时更接近原信号。

4. 音频实验

音频获取：使用matlab函数wavrecord()录制两端声音信号，设置录制频率FS=11025，并用wavplay()函数进行播放，使用wavwrite()函数将录制的音频文件存储为后缀名为wav的音频文件。

音频信号处理：将获取的音频信号进行数字化处理
首先画出两端信号的时域频谱图：

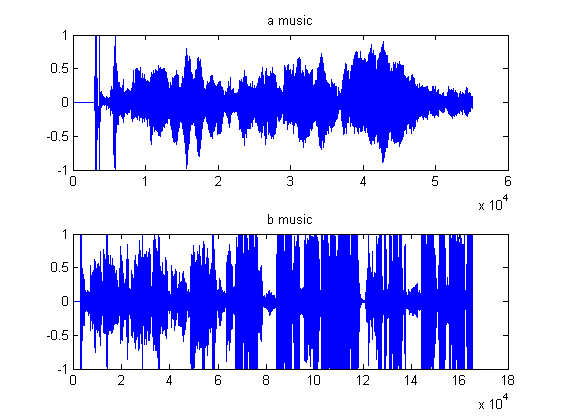
上面子图a music是a.wav文件的时域频谱图，下面子图b music是b.wav文件的时域频谱图。下面将两段声音信号进行合成，生成混音信号、和回声信号。

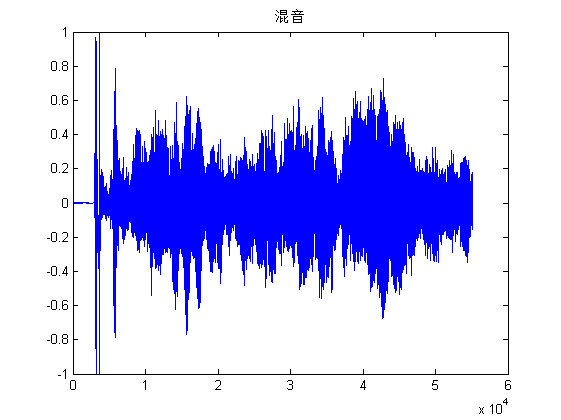
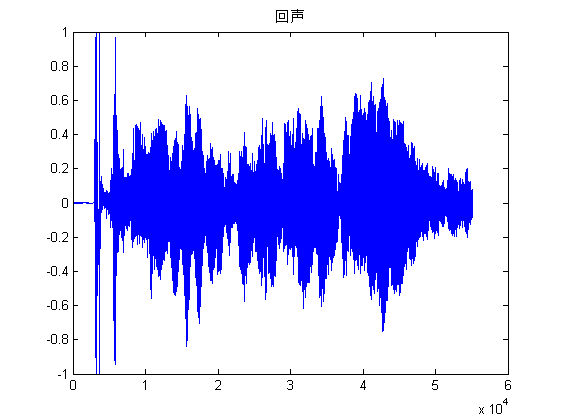
混声的产生是将两种声音信号线性变化得到的，此次实验中y1的系数为1，y2的系数为0.3。然后对产生的新信号进行归一化形成图5.1的混声。回声的产生原理是将不同时间段的声音信号进行线性变化。首先产生回声信息，然后将回声信息和原信息进行混合，就得到了回声信息。

总结

经过此次实验，学会使用matlab工具进行基本的信号处理。首先仿真出不同基本序列的图形，其次对奈奎斯特采样定理进行实验探究，进一步以实验的方式验证了奈奎斯特采样定理。同时又对截止频率对采样的影响进行了实验分析。最后实践操作录制音频信息，并进行混音、回声等操作。通过这次测试技术的实验，使我学到了不少实用的知识，更重要的是做实验的过程，思考问题的方法，这与做其他的实验是通用的，真正使我们受益匪浅。

今天的文章数字信号处理实验(一)分享到此就结束了，感谢您的阅读。