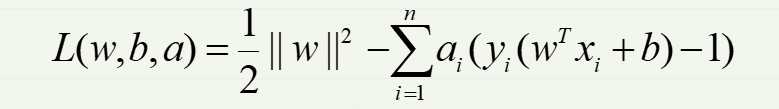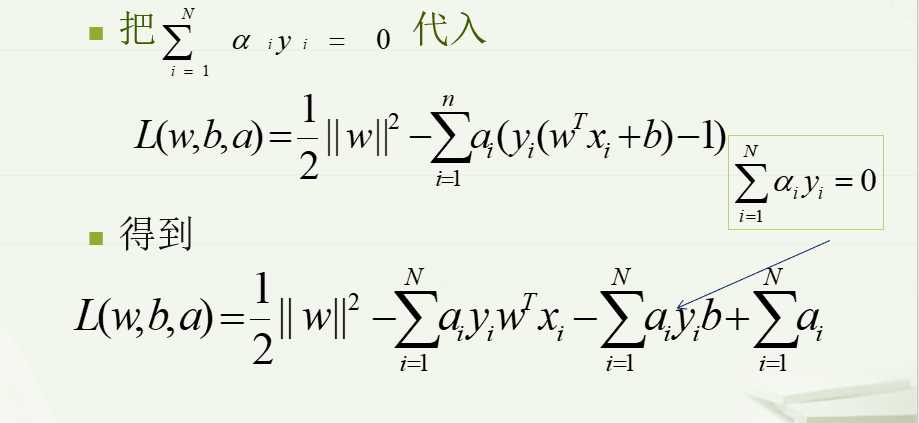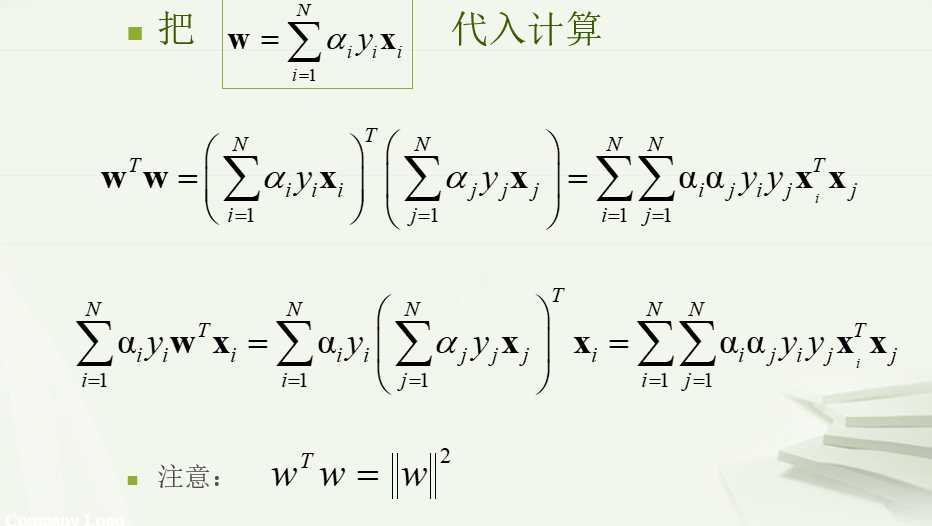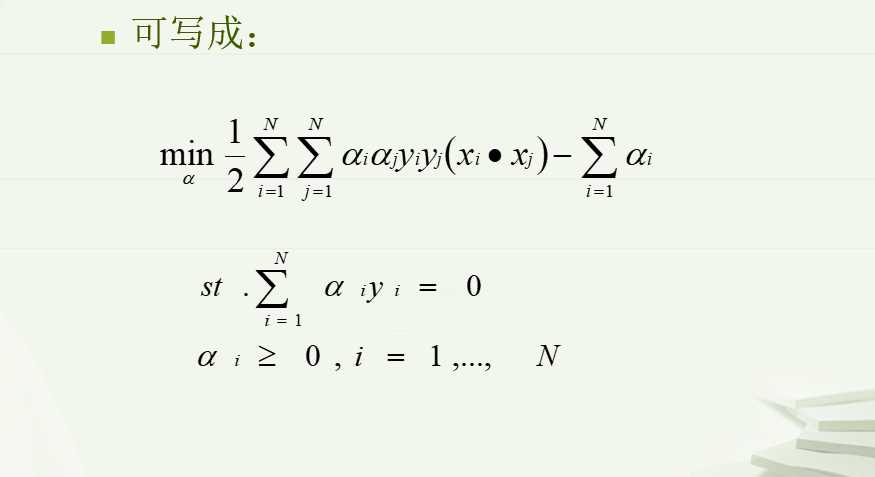基础:平面方程
在空间坐标系内,平面的方程均可用三元一次方程Ax+By+Cz+D=0来表示。
一、截距式
它与三
坐标轴的
交点分别为P(a,0,0),Q(0,b,0),R(0,0,c),其中,a,b,c依次称为该平面在x,y,z轴上的
截距。
坐标轴的
交点分别为P(a,0,0),Q(0,b,0),R(0,0,c),其中,a,b,c依次称为该平面在x,y,z轴上的
截距。
二、点法式
n为平面的法向量,
n=(A,B,C),M,M’为平面上任意两点,
则有n·MM’=0,
MM’=(x-x0,y-y0,z-z0),
n=(A,B,C),M,M’为平面上任意两点,
则有n·MM’=0,
MM’=(x-x0,y-y0,z-z0),
三点求平面可以取
向量积为
法线
向量积为
法线
任一
三元一次方程的图形总是一个平面,其中x,y,z的
系数就是该平面的一个
法向量的坐标。
三元一次方程的图形总是一个平面,其中x,y,z的
系数就是该平面的一个
法向量的坐标。
两平面互相垂直相当于A1A2+B1B2+C1C2=0
两平面平行或重合相当于A1/A2=B1/B2=C1/C2
点到平面的距离=abs(Ax0+By0+Cz0+D)/sqrt(A^2+B^2+C^2) 求解过程:面内外两点连线在法向量上的映射Prj(小n)(带箭头P1P0)=数量积
点到平面距离的证明过程:
三、一般式
四、法线式
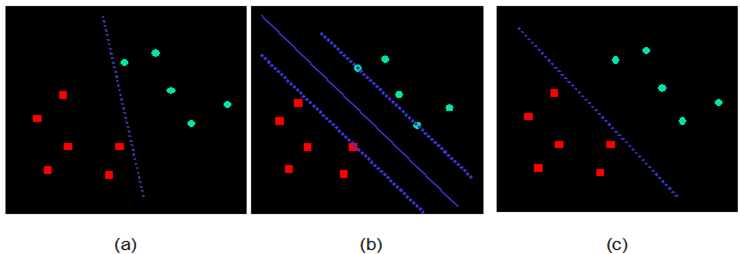
支持向量机
1.基础概要
支持向量机(support Vector Machine,SVN)是一种有监督的分类算法,通过探求风险最小来提高学习机的泛化能力,实现经验风险和置信范围的最小化。
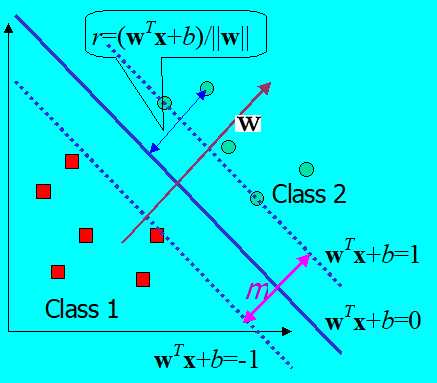
求解目标:求得一个最优超平面
其中W是超平面的法向量,决定了超平面的方向,b是位移项,决定了超平面到原点的距离。显然,超平面可以被W和b确定。样本空间任意一点到超平面的距离为W*X+B/||W||(点到距离的公式前面已经证明了)
如何求最优超平面(最大间隔分离超平面)?
基于目标函数和约束条件,定义拉格朗日函数:
今天的文章详解支持向量机。_支持向量机的作用分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/63858.html