数据结构-二叉树：给出前中后其中两种遍历顺序，如何求第三种？超详细解析

前言

大家好🌼🌼，我是 @愿此后再无WA，可以叫我小A🌀🌀，一位阳光帅小伙，对算法领域比较感兴趣。如果我的文章对您有用，欢迎持续关注，我们一起进步！🎈🎈

🔑最近刷题遇到了一个关于二叉树的问题，因为有些知识点比较模糊于是我又补了一下数据结构，看数据结构的过程中发现了 “在二叉树中，给出前中后其中两种遍历顺序，如何求第三种？” 这种问题，感觉挺重要的，于是我就记录了下来，也将自己的思路分享跟大家，希望对各位有所帮助。

二叉树的三种遍历方式

💡在解决上述问题前，我觉得有必要先说一下二叉树的三种遍历方式，它们分别是前序遍历，中序遍历和后序遍历。 这三种顺序的不同，取决于什么时候对父节点操作，如果先操作父节点然后是左子树最后时右子树那么就是前序，先左子树再父节点最后右子树就是中序，先左再右最后父就是后序遍历。注意，无论哪种顺序遍历，都必定先遍历左子树，然后再遍历右子树。这里的说的对父节点操作可以是打印父节点值，更改父节点的值等等。当然，除此之外常见的遍历方式还有层序遍历，但本篇主角是前三位。

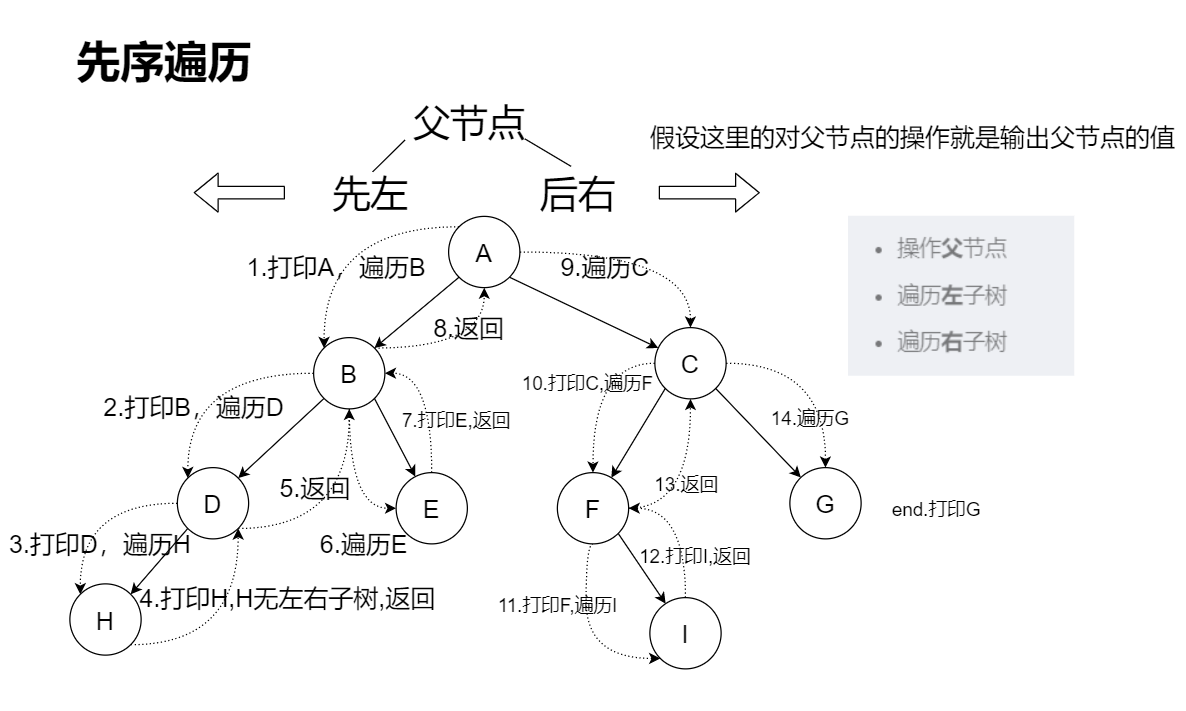
🌵前序遍历

• 操作父节点
• 遍历左子树
• 遍历右子树

我们结合图片看一下前序遍历的顺序。（这忘记署名了，然后没有保存，呜呜呜）

那么前序遍历的顺序应该是：ABDHECFIG

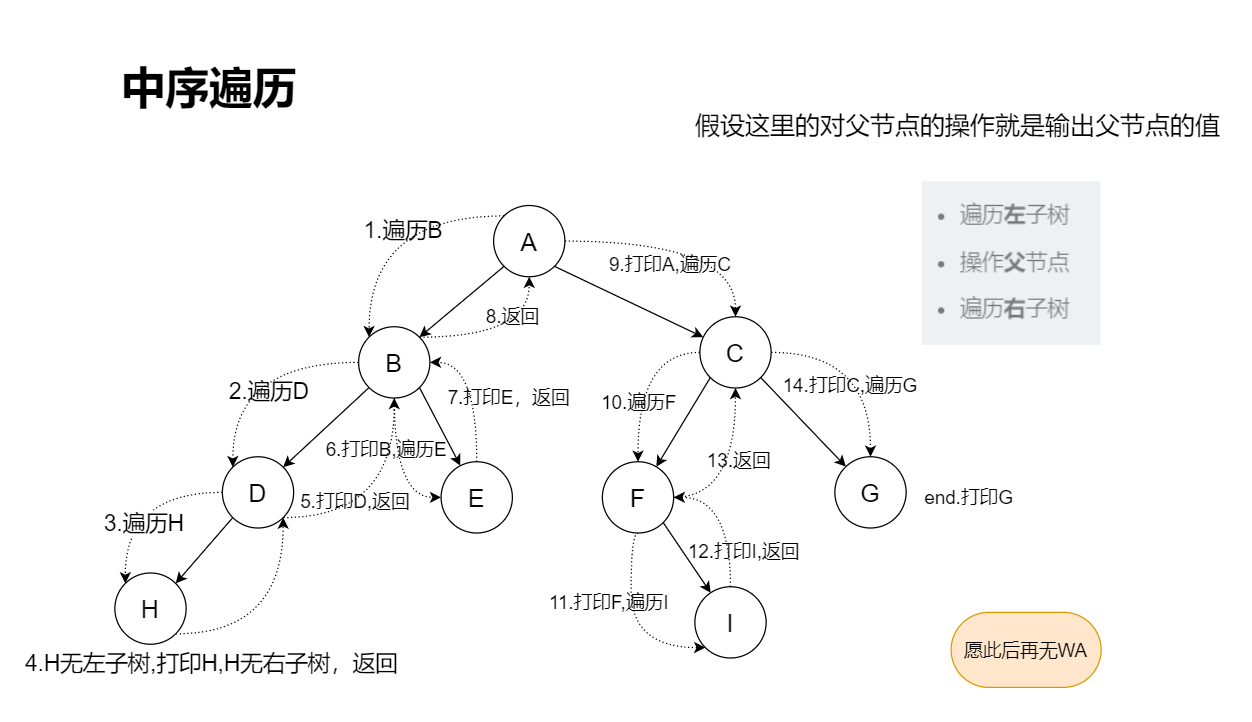
🌵中序遍历

• 遍历左子树
• 操作父节点
• 遍历右子树

我们结合图片看一下中序遍历的顺序。

中序遍历的顺序是: HDBEAFICG

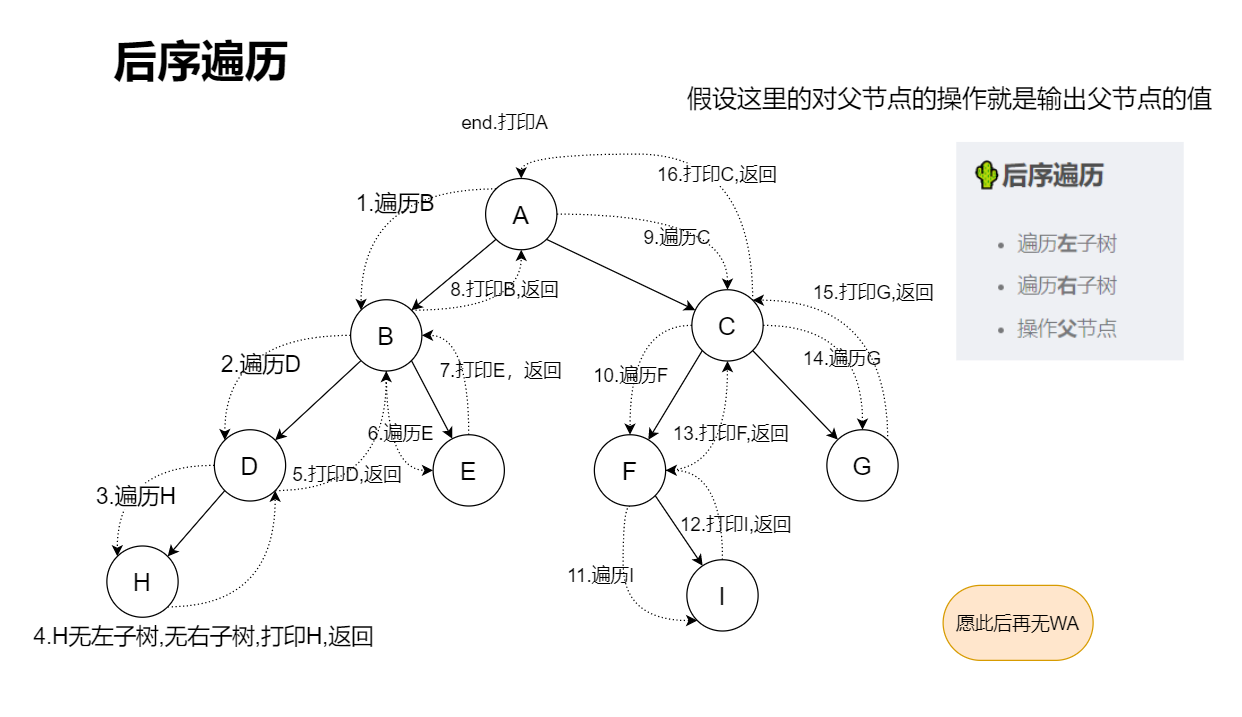
🌵后序遍历

• 遍历左子树
• 遍历右子树
• 操作父节点

最后我们结合图片看一下后序遍历的顺序。

后序遍历的顺序是：HDEBIFGCA

知二求一

🌳当了解以上这三种遍历方式后，就会发现其实他们之间就只有细微的差别而已，我作图是深感体会的，前面两张的箭头线条我没有更改，仅仅只是更改了些文字而已，后序遍历稍有不同，因为要回到起点就会多两个箭头，不仅如此，后面两种遍历方式的排版我也是直接从复制前序遍历的，只需要改一两处就好了。

前中求后

🍀已知一棵二叉树的前序遍历序列为 ABCDEF 中序遍历序列为 CBAEDF ，请问这棵二叉树的后序遍历结果是多少?

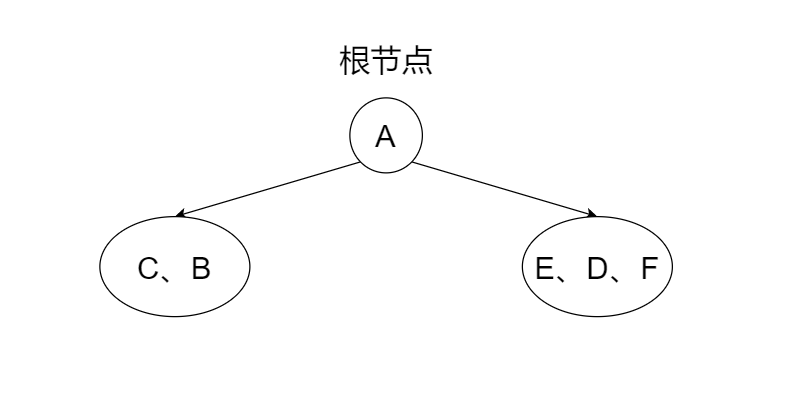
🌱第一步，找根节点。根据前序遍历的性质可知，首先访问的就是根节点。因为前序遍历序列第一个元素是A，因此，A是这棵树的根节点。

🌱第二步，划分左右子树。我们已经知道了哪个是根节点，结合题目给出的中序序列可知CB在A的左边，EDF在A的右边，那么可以将将他们划分开。

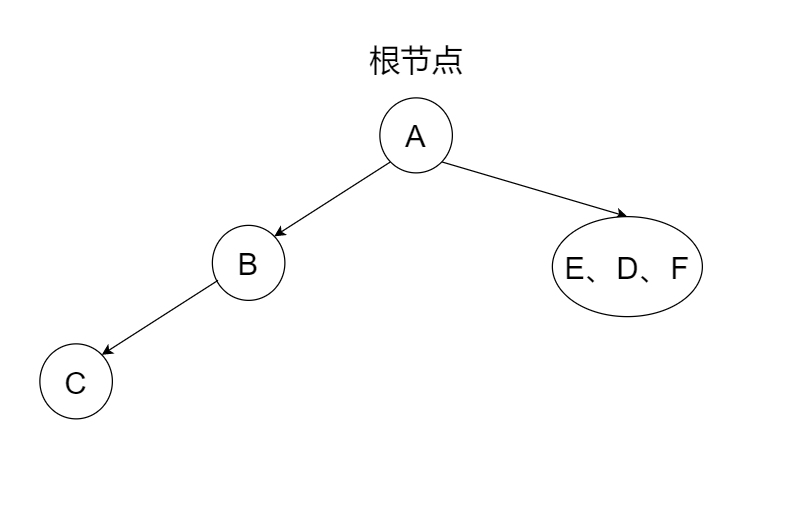
🌱第三步，循环执行1、2步骤。我们回顾一下题目“前序遍历序列为 ABCDEF 中序遍历序列为 CBAEDF”。先看前序序列，A接着是B，那么B就是这棵左子树的根节点，然后看中序序列，那么B左边的元素就是B的左子树（仅有C），B右边A左边的元素就是B的右子树(无)，因为数据较少，所以现在已经得出答案了，因此A的左子树的结构是这样的。

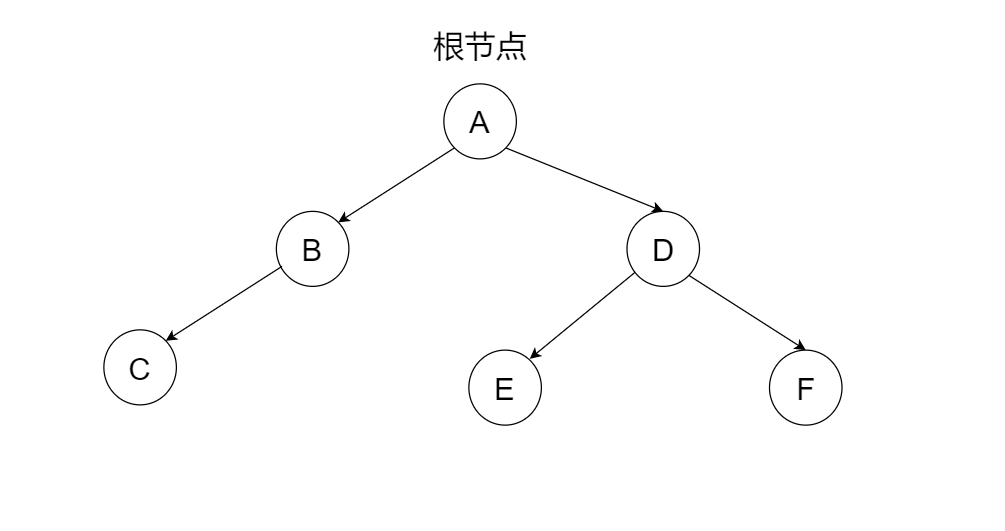
接着看A的右子树。在前序序列 ABCDEF中BC已经选完了，所以D就是A的右子树根节点。然后看中序序列CBAEDF，以D为根节点划分左右子树。所以D的左子树是E,右子树是F。因此，根据前序中序遍历得出的二叉树是这样的。（你以为这就结束了吗？没有，还要检查❗️❗️）

🎯既然已经知道了二叉树的结构，我们就能得出后序遍历的顺序了，是：CBEFDA

📌📌看完以上思路你是否能得出什么技巧？没错，可以知道，前序序列是用来找子树根节点的，中序序列是用来划分左右子树的。

📝📝我们做一道练习题巩固一下。

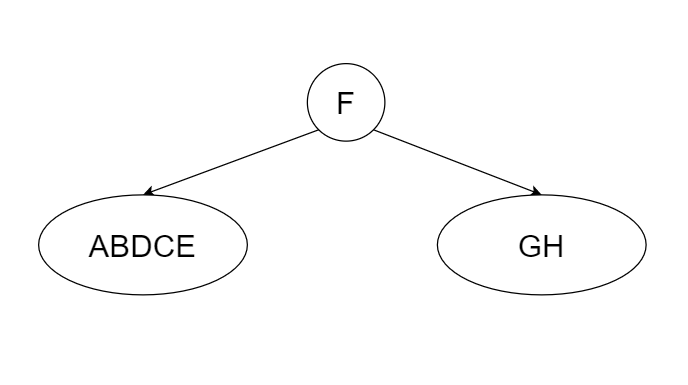
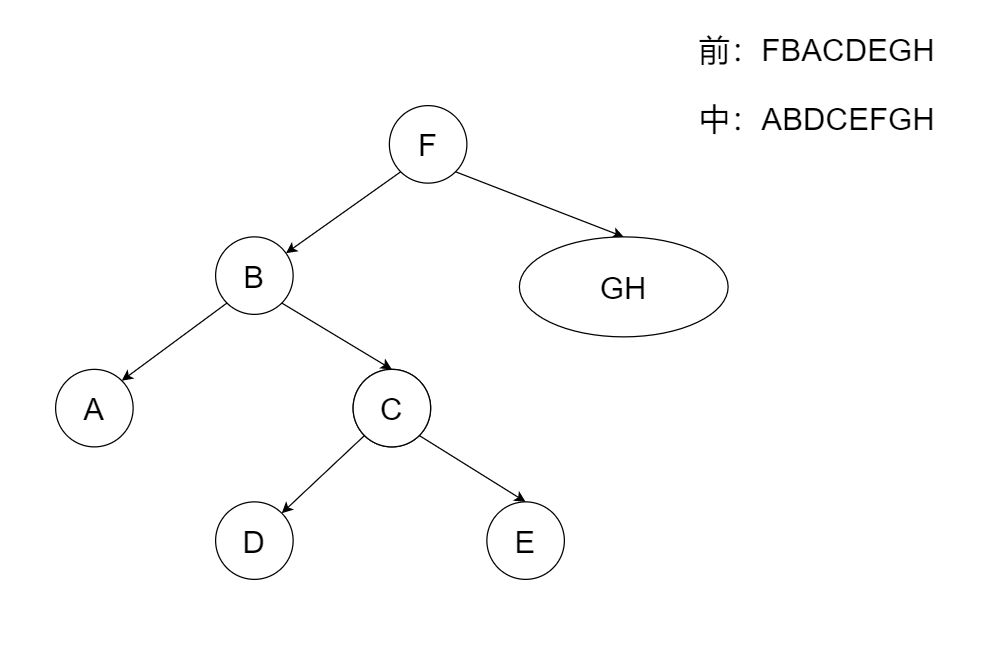
老样子找根节点，容易知道根节点是F,接着看中序遍历划分F的左右子树

看前序序列选左子树的根节点，F接着是B,所以B是F的左子树根节点。然后看中序序列划分B的左右子树，B的左子树是A,右子树是DCE,然后看前序序列，FBA都选过了，接着就是C,所以C是B右子树的根节点，重复上面步骤，可以得出F的左子树结构是：

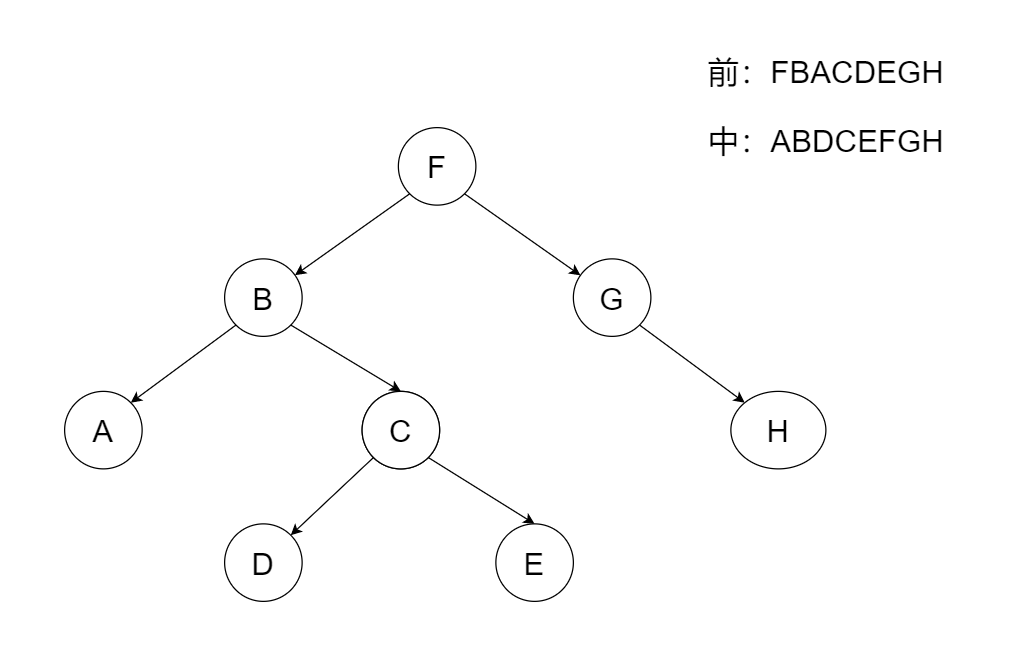
接着看F的右子树，在先序遍历中其他元素已经确定了，G在H的前面，因此，F的右子树的根节点是G，接着看中序序列H在G的右边，因此H是G的右子树。那么完整的二叉树结构是：

🎯🎯最后，根据该结构可以知道后序遍历的顺序是：ADECBHGF。

后中求前

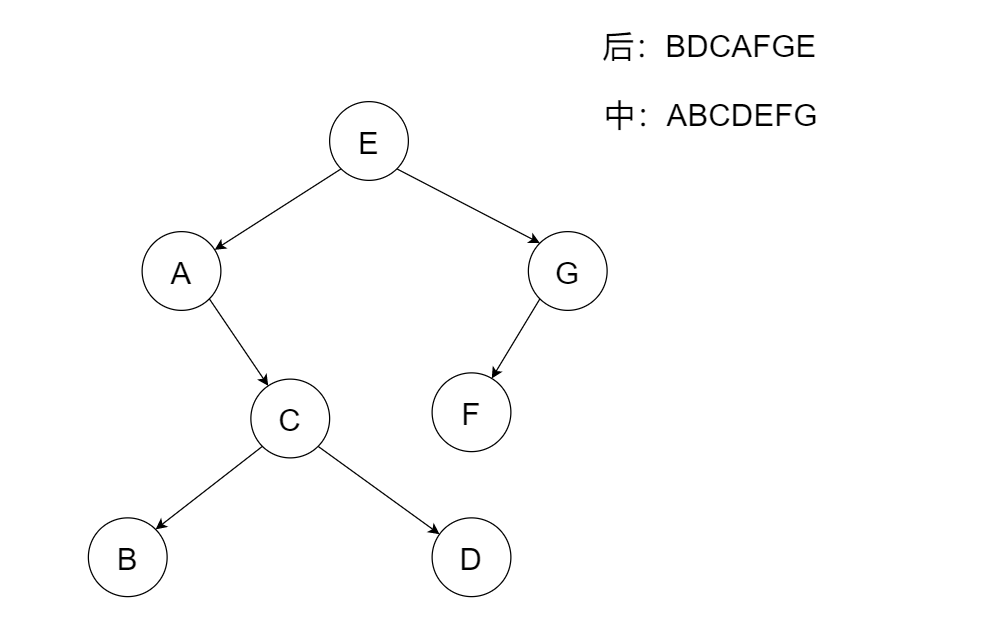
🍀已知二叉树的中序序列是 ABCDEFG ，后序序列是 BDCAFGE ，问前序序列是多少？

⭐️⭐️ 同样的，第一步找根节点，第二步划分左右子树，第三步，重复上面1、2步骤。 因为划分左右子树都是根据中序序列划分的，因此方法还是与 前中求后 中的划分方法一致，不同的是找根节点的方法，这里是在后序序列中找的。我们知道，在后序序列中，每棵树的根节点总是最后出现的，所以我们可以以此为突破点作为确定根节点的方法。

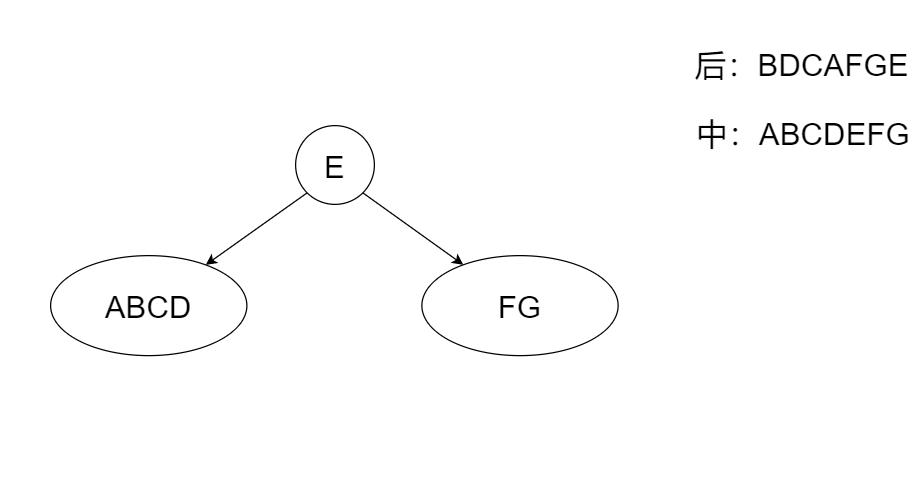
⛳️ 好，回到题目，因为在后序序列中根节点总是最后出现的，因此，E是根节点。确定了根节点后，接着就是划分左右子树了。在中序序列中，ABCD位于E的左侧，FG位于E的右侧，那么二叉树的大致形状是这样的。

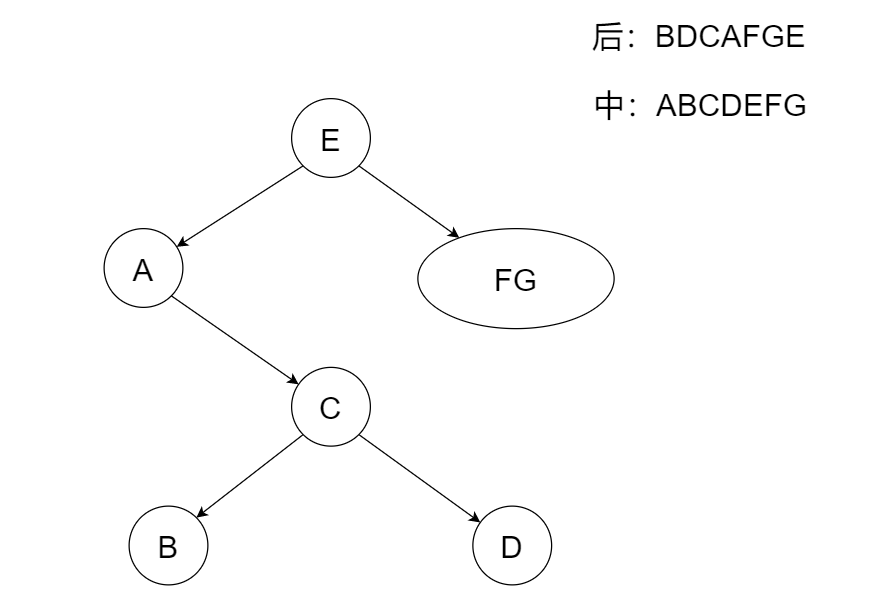
⛳️ 继续找根节点，先从E的左子树开始，看后序序列“BDCAFGE”，E的左子树有ABCD四个元素，而这四个元素中A元素最后出现的，因此就是A就是E左子树的根节点。选完根节点后就要划分子树，看中序序列，BCD全在A的右侧。然后在BCD中选择根节点，看后序序列，C在BCD中最后出现，因此C是A的右子树节点，最后看中序序列可以知道BD分别位于C的左侧跟右侧，那么E的左子树结构是这样的。

⛳️ 现在我们看一下E的右子树，其实左子树已经出来了的话，右子树很容易判断了，因为还有GF两个节点。老规矩，先找出右子树的根节点，看后序序列，G在F的后面，因此，G应该是E的右子树根节点，最后最后，看中序序列，F在G的左侧，因此完整的的二叉树结构是这样的。

⛳️ 接着干啥？检查。检查发现好像没有什么问题，那么我们就能根据该二叉树结构得出前序序列了。前序序列应该是EACBDGF。

📝清楚了求解过程之后当然就要巩固啦！这里我给出一道练习题和答案大家课下练习哈，熟能生巧呀，我这里就不一一演示咯。😁😁

📝eg：已知二叉树的中序遍历顺序为DBAGEHCF，后序遍历顺序为DBGHEFCA，求该二叉树的前序遍历。 答案：ABDCEGHF

前后求中

🍀我们已经知道了前面两种求法，现在来看一下第三种。

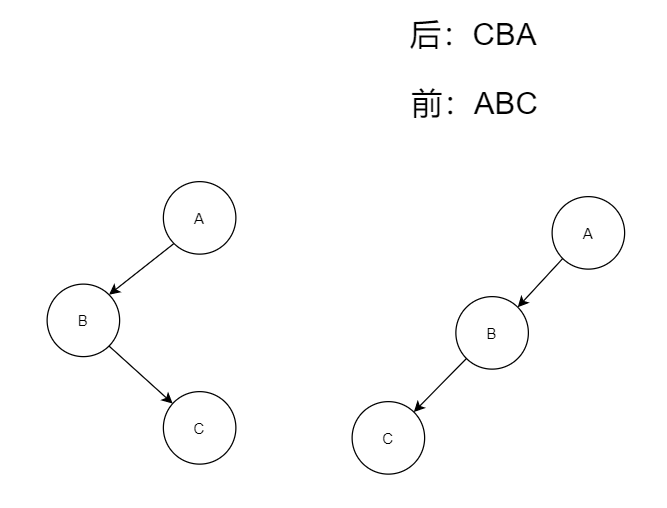
📝 已知前序序列ABC与后序序列CBA，求中序序列。

💨我们想想这题该怎么求？可能有同学会说，出这么简单的题，不用想也求得出来吧，随便画两下就有了！那确实也对呀，我们现在就画画吧。

✌️我们就先画两种，其实应该不止两种的，这两种结构的二叉树前序和后序都一样都是前：ABC，后：CBA。我们知道，二叉树是讲究顺序的，顺序不同，表示的二叉树也就不同。因此，我们无法通过先序与后序序列来求解中序序列。

结论

基于以上三种求解方式，我们可以得出以下结论。

❄️己知前序序列和中序序列，可以唯一确定一棵二叉树。

❄️已知后序序列和中序序列，可以唯一确定一棵二叉树。

💢已知前序序列和后序序列，不能够确定一棵二叉树。

最后

🐑这篇知识点已经讲完啦，不知道同学们理解的怎么样呢？有任何疑惑的地方都能够在下方评论区留言哦，感谢观看🔔🔔我们下期见。

今天的文章数据结构-二叉树：给出前中后其中两种遍历顺序，如何求第三种？超详细解析分享到此就结束了，感谢您的阅读。