TrailingZeros——Leetcode 0172 寻找尾零的数目

题目描述

Given an integer n, return the number of trailing zeroes in n!.

Note that $n!=n\ast (n-1)\ast (n-2)\ast ...\ast 3\ast 2\ast 1.$

Example1

Input: n = 3
Output: 0
Explanation: 3! = 6, no trailing zero.

Example2

Input: n = 5
Output: 1
Explanation: 5! = 120, one trailing zero.

Example3

Input: n = 0
Output: 0

Constraints

• $0<=n<=10^4$

题解

题目分析：题目要求求出任意给定一个正整数n的阶乘的尾零个数，例如Example2中给出的那样，$5!=120$，因此尾零个数即为1。
看到这里，相信许多同学已经跃跃欲试，那我直接求解$n!$然后把结果中尾零的个数求出来不就完事儿了？上代码：

class Solution:
    def fact(self, n):
        if n == 1:
            return n
        return n * self.fact(n - 1)

    def trailingZeroes(self, n: int) -> int:
        result = self.fact(n)
        bits = list(str(result))
        i = len(bits) - 1

        while bits[i] == '0':
            i -= 1

        return len(bits) - 1 - i

以上代码给出了本题最直接的解法，很容易便可以求出尾零的个数。可惜天不遂人愿，我们看题目给出的约束，即$n<10^4$，可以想象如果给定的$n=10000$那么在求解上述阶乘时就直接原地爆炸堆栈溢出，我们用的栈太多了。实际上，不需要$n=10000$，我们给定一个较大的$n$时编译器会告诉我们实际上可以允许的堆栈到底有多少，上图：

事实上当递归次数超过图中圈画的次数时，递归将会被强制停止。。。因此以上方法虽然理论上可行，但是真正实现时其只允许数字不超过$n=997$（还好不是996…），因此我们需要重新考虑。求出尾零的个数，是不是必须要把最后的结果求出来呢？

非也

这道题从考察角度出发并不是为了让我们写上面的递归程序，而是考察我们的数学理解能力。我们知道只有在乘法中出现$10$时，尾部才会增加一个$0$，因此我们需要考虑的是如何运算才会出现$10$，很简单，对其做质因数分解，我们知道$10=5\times 2$，因此对每一项做质因数分解找到其中的$2,5$对的个数，即为尾零的数目。
针对Example2给出的例子：
$$5!=(5\ast 1)\ast (2\ast 2)\ast (3\ast 1)\ast (2\ast 1)\ast 1$$
可以发现，其中$5,2$只出现了一对。另一个很容易发现的点是，2的数目远远多于5的个数，因此我们只需要求取$5$出现的次数即可，上代码：

class Solution:
    def find_factor_five(self, n):
        # 求取n的质因数中5的个数
        counter = 0
        while n % 5 == 0:
            n /= 5
            counter += 1

        return counter

    def trailingZeroes(self, n: int) -> int:
        # 统计5的个数
        counter = 0
        if n < 5:
            return counter
        while n > 5:
            n_factor_five = self.find_factor_five(n)
            n -= 1
            counter += n_factor_five
        return counter + 1

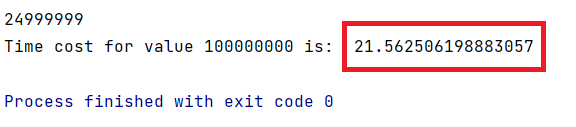
上述代码非常清楚的阐释了上面所说的一堆废话。但是这是不是就是最佳的求解方法呢？事实上，针对题目给出的限制该方法已足够Pass所有测试用例，但是当$n$的值取得更大时（比如一个小目标），我们会发现上述方法计算时间也是非常可观：

单位是$s$！，所以上述方法是不是还有改进的余地呢？
Leetcode上的老哥@Wang给出了一个更加迅速的方法。
我们重新分析，在从$1$计数到$n$的过程中，我们会发现其实$5$的出现是有规律的，其只会出现在$5,10,15,20,...$这些数字中，即每隔$5$个数字会出现一次，但是值得注意的是每隔$5^2$会出现2个$5$，每隔$5^3$会出现3个$5$，不难发现，我们所要求取的$5$的个数其实只需要按照上述规律计数即可，上代码：

class Solution:
    def find_factor_five(self, n):
        # 求取n的质因数中5的个数
        counter = 0
        while n % 5 == 0:
            n /= 5
            counter += 1

        return counter

    def trailingZeroes(self, n: int) -> int:
        # 统计5的个数
        counter = 0
        if n < 5:
            return counter
        while n > 5:
            n_factor_five = self.find_factor_five(n)
            n -= 1
            counter += n_factor_five
        return counter + 1
    def trailingZeroes_Count(self, n: int) -> int:
        counter = 0
        # 直接计数！
        while n / 5 > 1:
            counter += int(n / 5)
            n /= 5
        return counter


s = Solution()
start = time.time()
n = 100000000
print(s.trailingZeroes_Count(n))
end = time.time()
print(f"Time cost for value { 
     n} is: ", end - start)

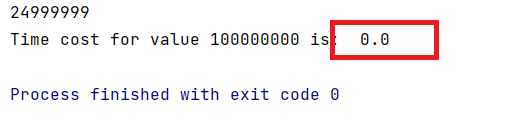
对比一下时间…

这可不是吹出来的兄弟萌，牛逼！

今天的文章TrailingZeros——Leetcode 0172 寻找尾零的数目分享到此就结束了，感谢您的阅读。