最长对称子串（马拉车算法）

马拉车算法：

一）第一步是改造字符串 S，变为 T，其改造的方法如下：

在字符串 S 的字符之间和 S 的首尾都插入一个 ‘#’，如：S=“abba”变为 T=”#a#b#b#a#” 。我们会发现 S 的长度是 4，而 T的长度为 9，长度变为奇数了！！那 S 的长度为奇数的情况时，变化后的长度还是奇数吗？我们举个例子，S=“abcba” 变化为 T=“#a#b#c#b#a#”，T 的长度为 11，所以我们发现其改造的目的是将字符串的长度变为奇数，这样就可以统一的处理奇偶的情况了。

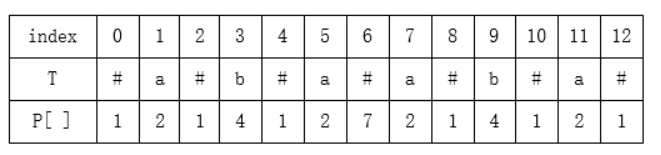
二）第二步，为了改进回文相互重叠的情况，我们将改造完后的 T[i] 处的回文半径存储到数组 P[i] 中，P[i] 为新字符串 T 的T[i] 处的回文半径，表示以字符T[i]为中心的最长回文字串的最端右字符到 T[i] 的长度，如以 T[i] 为中心的最长回文子串的为T[l,r]，那么 P[i]=r-i+1。这样最后遍历数组 P[i]，取其中最大值即可。若 P[i]=1 表示该回文串就是 T[i] 本身。举一个简单的例子感受一下：

数组P有一性质，P[i]-1 就是该回文子串在原字符串 S 中的长度，那就是 P[i]-1 就是该回文子串在原字符串 S 中的长度，至于证明，首先在转换得到的字符串 T 中，所有的回文字串的长度都为奇数，那么对于以 T[i] 为中心的最长回文字串，其长度就为 2*P[i]-1,经过观察可知，T 中所有的回文子串，其中分隔符的数量一定比其他字符的数量多 1，也就是有 P[i] 个分隔符，剩下 P[i]-1 个字符来自原字符串，所以该回文串在原字符串中的长度就为 P[i]-1。

另外，由于第一个和最后一个字符都是 ‘#’ ，且也需要搜索回文，为了防止越界，我们还需要在首尾再加上非#号字符，实际操作时我们只需给开头加上个非 ‘#’ 号字符，结尾不用加的原因是字符串的结尾标识为 ‘\0’，等于默认加过了。这样原问题就转化成如何求数组 P[i] 的问题了。

三）如何求数组 P[i]

  从左往右计算数组 P[ ]，Mi 为之前取得最大回文串的中心位置，而R是最大回文串能到达的最右端的值。

  1）当 i<=R 时，如何计算 P[i] 的值了？毫无疑问的是数组P中点 i 之前点对应的值都已经计算出来了。利用回文串的特性，我们找到点 i 关于 Mi 的对称点 j，其值为 j=2*Mi-i 。因点 j 、i 在以 Mi 为中心的最大回文串的范围内[L ,R]。

       a）那么如果 P[j] <R-i （同样是 L 和 j 之间的距离），说明，以点 j 为中心的回文串没有超出范围 [L ,R]，由回文串的特性可知，从左右两端向 Mi 遍历，两端对应的字符都是相等的，即 P[j]=P[i]（这里得先从点j转到点 i 的情况）。

       b）如果 P[j]>=R-i (即 j 为中心的回文串的最左端超过 L)，即以点 j 为中心的最大回文串的范围已经超出了范围 [L,R] ，这种情况，等式 P[j]=P[i] 还成立吗？显然不总是成立的！因以点 j 为中心的回文串的最左端超过L，那么在[L, j]之间的字符肯定能在 [j, Mi] 找到相等的，由回文串的特性可知，P[i] 至少等于 R- i，至于是否大于 R-i，我们还要从 R+1 开始一一的匹配，直达失配为止，从而更新 R 和对应的 Mi 以及 P[i]。

 2）当 i > R时，没法利用到回文串的特性，只能老老实实的一步步去匹配。

                                              L2-008 最长对称子串 

对给定的字符串，本题要求你输出最长对称子串的长度。例如，给定Is PAT&TAP symmetric?，最长对称子串为s PAT&TAP s，于是你应该输出11。

输入格式：

输入在一行中给出长度不超过1000的非空字符串。

输出格式：

在一行中输出最长对称子串的长度。

输入样例：

Is PAT&TAP symmetric?

输出样例：

11

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 10000005;

int v[maxn];
char str[maxn];

int main()
{
	string s;
	int cnt = 2;
	getline(cin,s);
	str[0] = '$';
	str[1] = '#';
	for(int i=0; i<s.size(); i++){
		str[cnt++] = s[i];
		str[cnt++] = '#';
	}
	str[cnt++] = '\n';
	int id=0,mx=0,maxlen=0;
	for(int i=0; i<cnt; i++){
		if(mx>i) v[i] = min(v[2*id-i],mx-i);
		else v[i] = 1;
		while(str[i+v[i]] == str[i-v[i]]) v[i]++;
		if(i+v[i] > mx){
			mx = i+v[i];
			id = i;
		}
		maxlen = max(v[i]-1,maxlen);
	}
	cout << maxlen << endl;
	return 0;
}

参考链接：http://www.cnblogs.com/yfz1552800131/p/8640825.html

今天的文章最长对称子串（马拉车算法）分享到此就结束了，感谢您的阅读。