K均值聚类(K-means)
图片出处
本篇将介绍无监督学习家族中的一种经典聚类算法——K均值聚类(K-means)。
文章目录
导论
期末考试结束了,小明同学的数学和英语成绩在60-70分之间,其中,数学成绩为62分,英语成绩为65分。小明的班上一共有15名学生,如果小明的数学和英语成绩达到了班级“中游水平”, 他就可以受到表扬,但是如果他是“须努力“的学生,那小明就会被爸爸批评。小明认为他是班级里”中等水平“的学生,但是小明的爸爸认为儿子属于“须努力”的水平。两个人争执不下,各自振振有词。
我们想要确定的是,小明到底属于哪一类学生。因为每一次考试的难度不一样,题目不一样,小明和爸爸心中对于成绩好坏的标准也不一样,所以我们并不能凭借上一次考试的分数和小明或者爸爸一方的说法来简单地认为小明到底是什么水平的学生。我们希望有一种较为公平公正的评价方式,来合理地将同学们分成几个档次。解决这一类问题,我们就可以用K均值聚类(K-means)。
什么是K-means
在机器学习中,无监督学习一直是我们追求的方向,而其中的聚类算法更是发现隐藏数据结构与知识的有效手段。目前如谷歌新闻等很多应用都将聚类算法作为主要的实现手段,它们能利用大量的未标注数据构建强大的主题聚类。
给定一组数据点,我们可以用聚类算法将每个数据点分到特定的组中。理论上,属于同一组的数据点应该有相似的属性和/或特征,而属于不同组的数据点应该有非常不同的属性和/或特征1。
K-means是机器学习中一个比较常用的算法,属于无监督学习算法,其常被用于数据的聚类。我们将每一个类称为一个簇,将每一个簇的中心称为质心。运用K-means算法时,我们只需要指定簇(或称,聚类)的数量 K K K 即可自动将数据聚合到多类中。
- 相同簇中的数据相似度较高,不同簇中数据相似度较低。
- 各个簇本身尽可能的紧凑,而各个簇之间尽可能地分开。
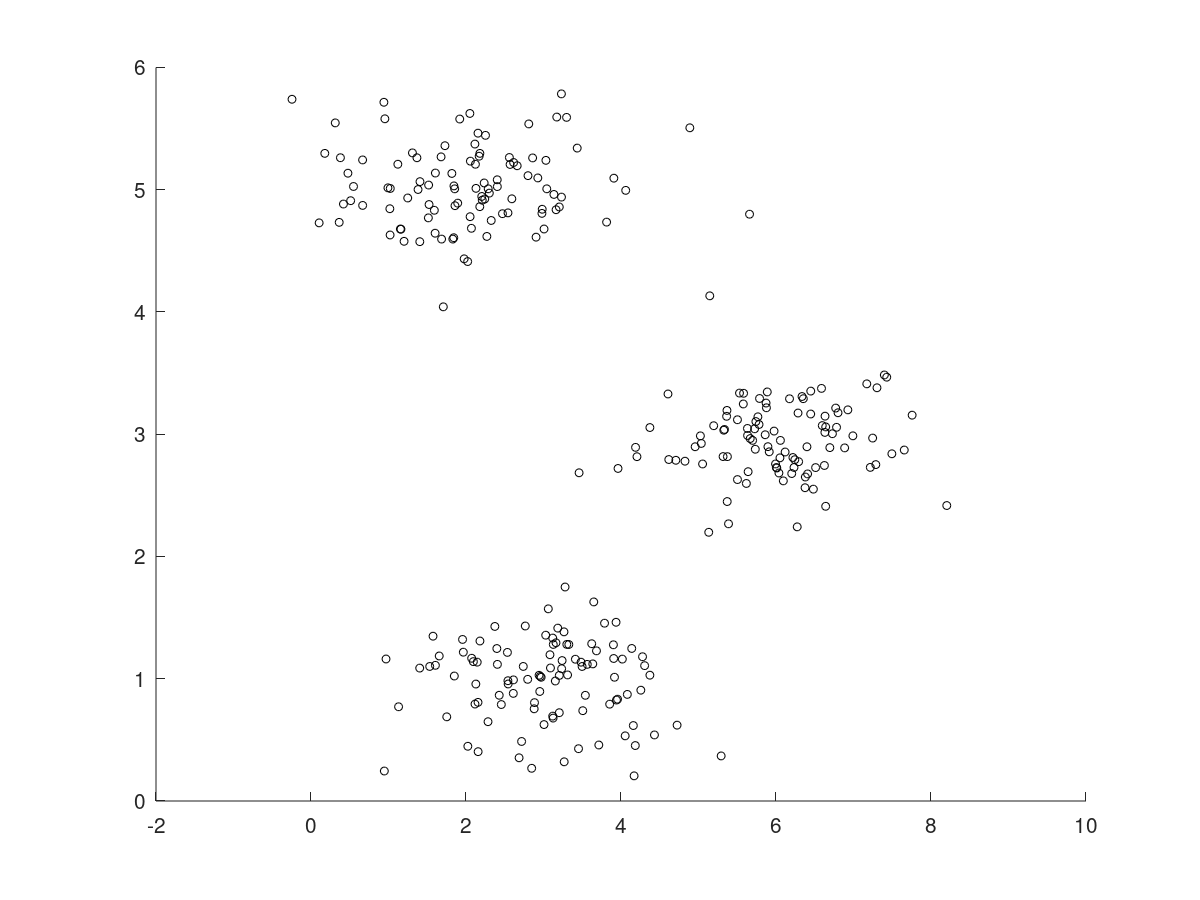
假设我们有一张这样的散点图1:
图1 散点图
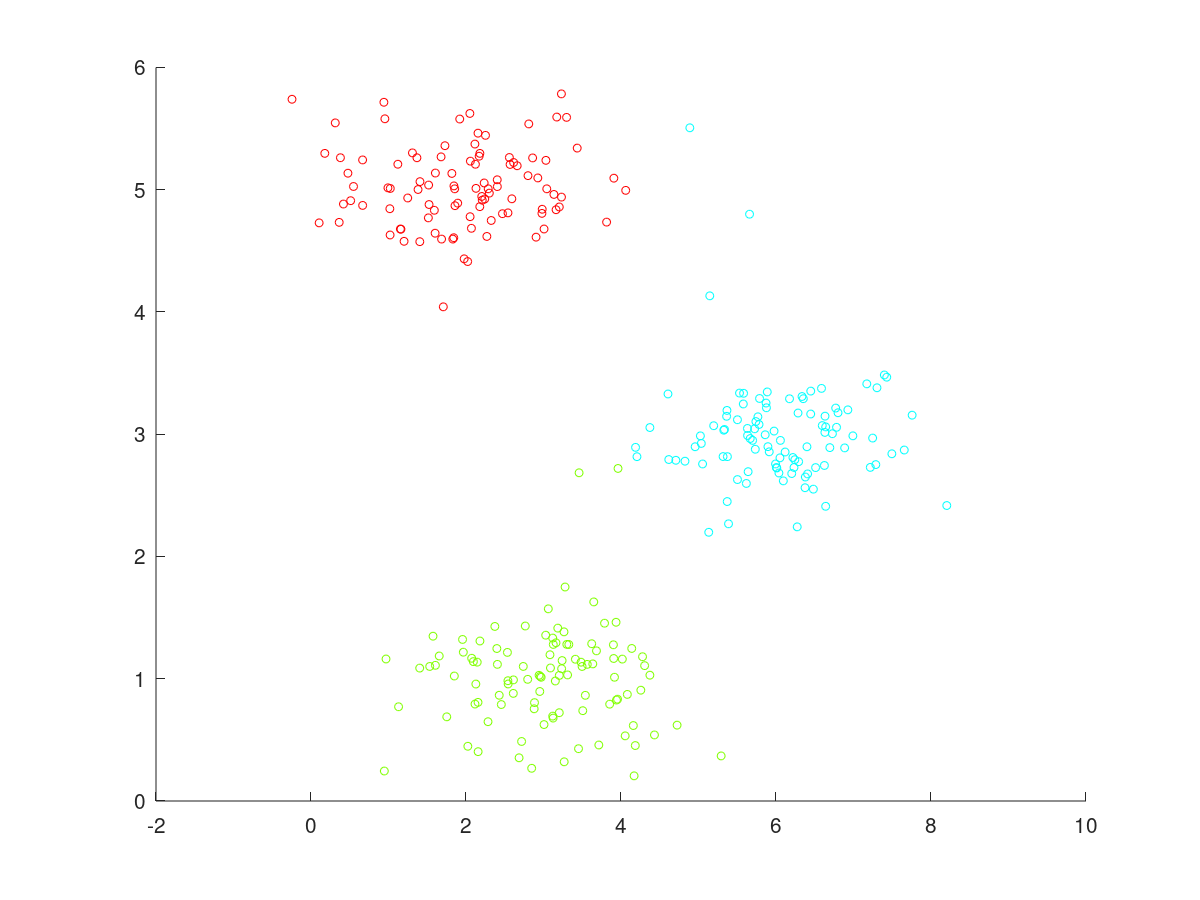
这些点本身是没有标记类别的,但基于点的分布状况,我们可以初步猜测这些点应该分属于三个不同类别。下面,我们指定有 K = 3 K=3 K=3 个簇,通过K-means算法即可以得到如下图 2 所示的分类结果。可见,数据点被完美地划分为 3 个类别,其中,每种颜色代表一种不同的类别。
图2 K-means算法指定K=3的分类结果
- K-means的优点是原理简单,运算速度快,能够较好地聚类大数据集。
- K-means的缺点是需要一开始就指定一个聚类数量 K K K,数据集中的异常值和聚类初始质心都会较大地影响聚类结果。
K-means的操作步骤
下面我们来具体看一下,上述分类过程是如何实现的。
K-means背后的原理直观上理解是一个迭代过程,首先人为设定 K K K个初始质心(或称,聚类中心),然后通过不断将新的样本分配至离它们最近的质心的方法优化调整质心位置,每次分配后都需要根据类内的样本重新计算质心坐标。
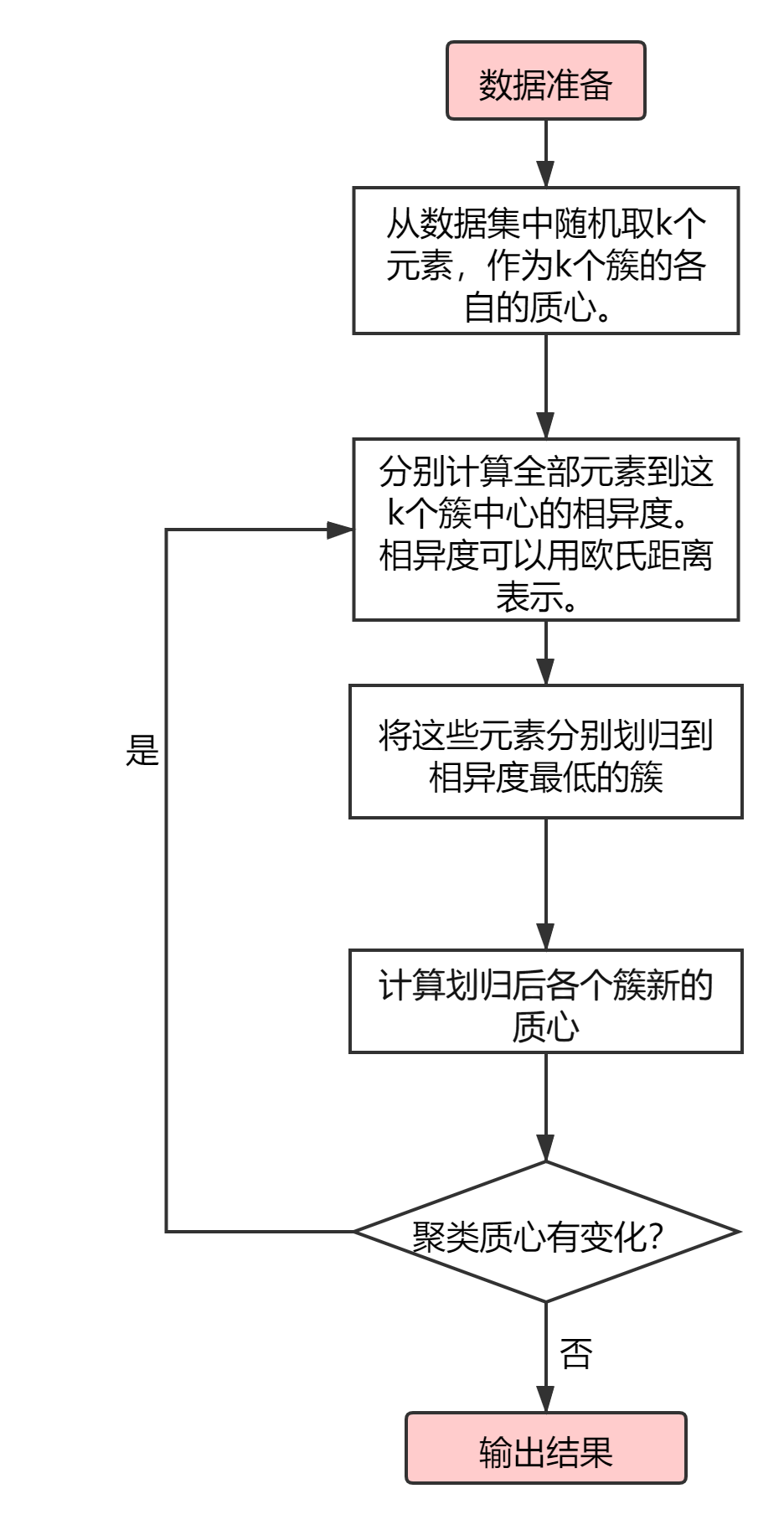
K-means算法流程如下图3所示2:
图3 K-means流程图
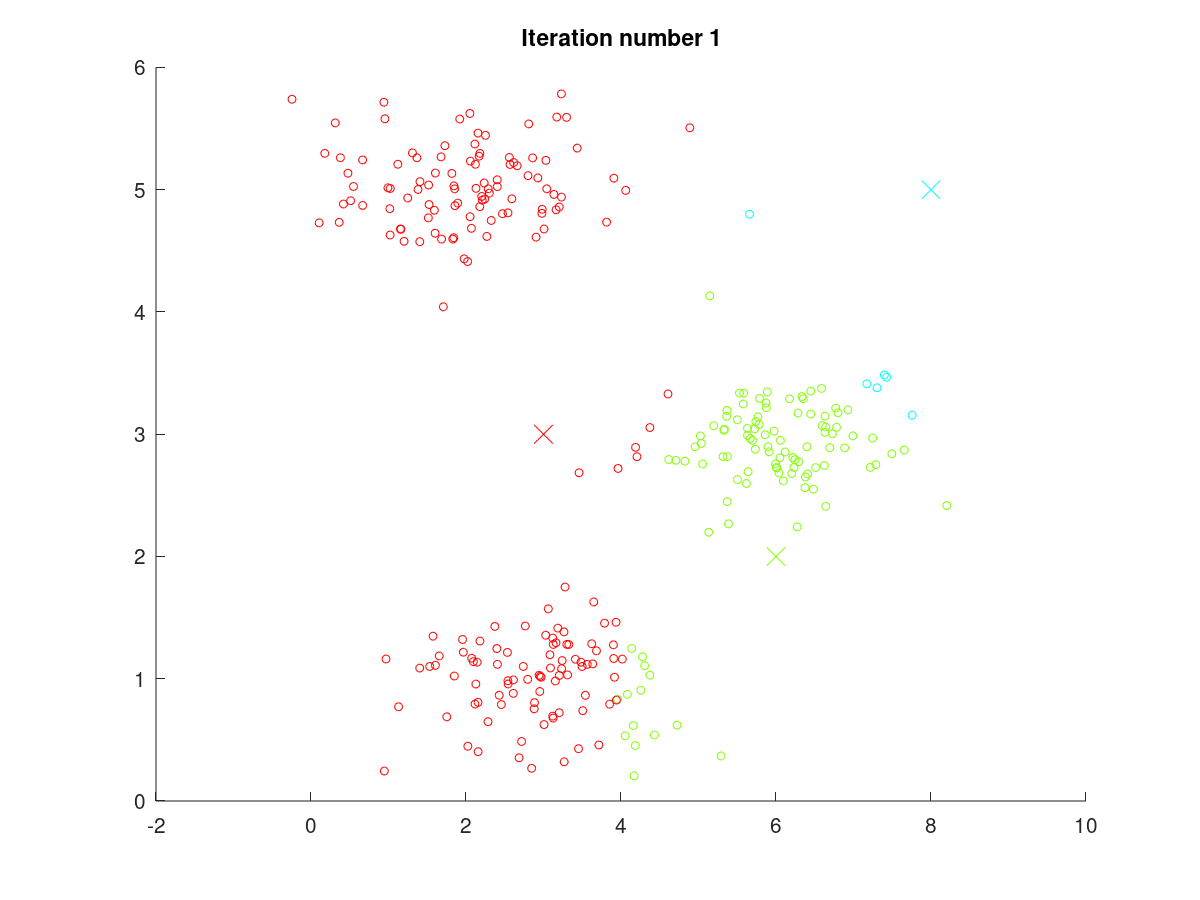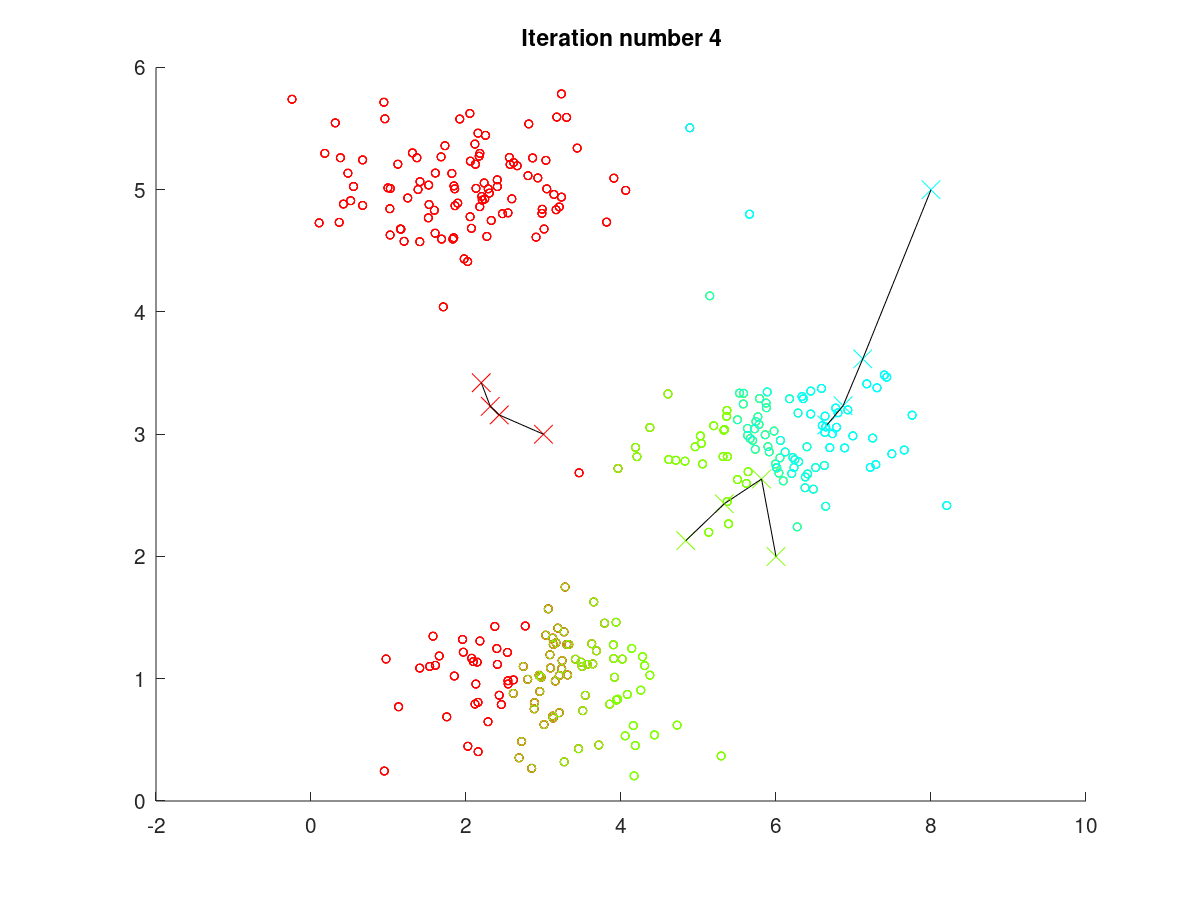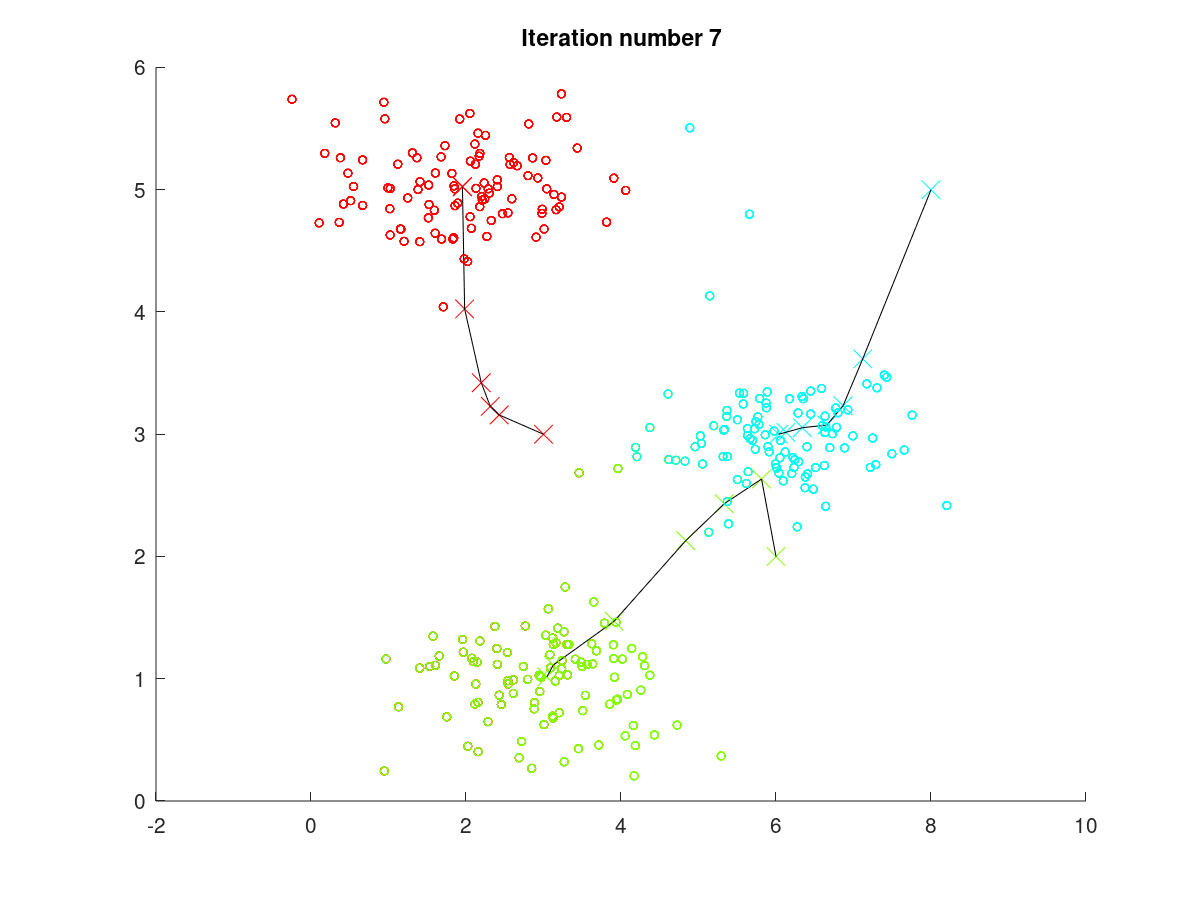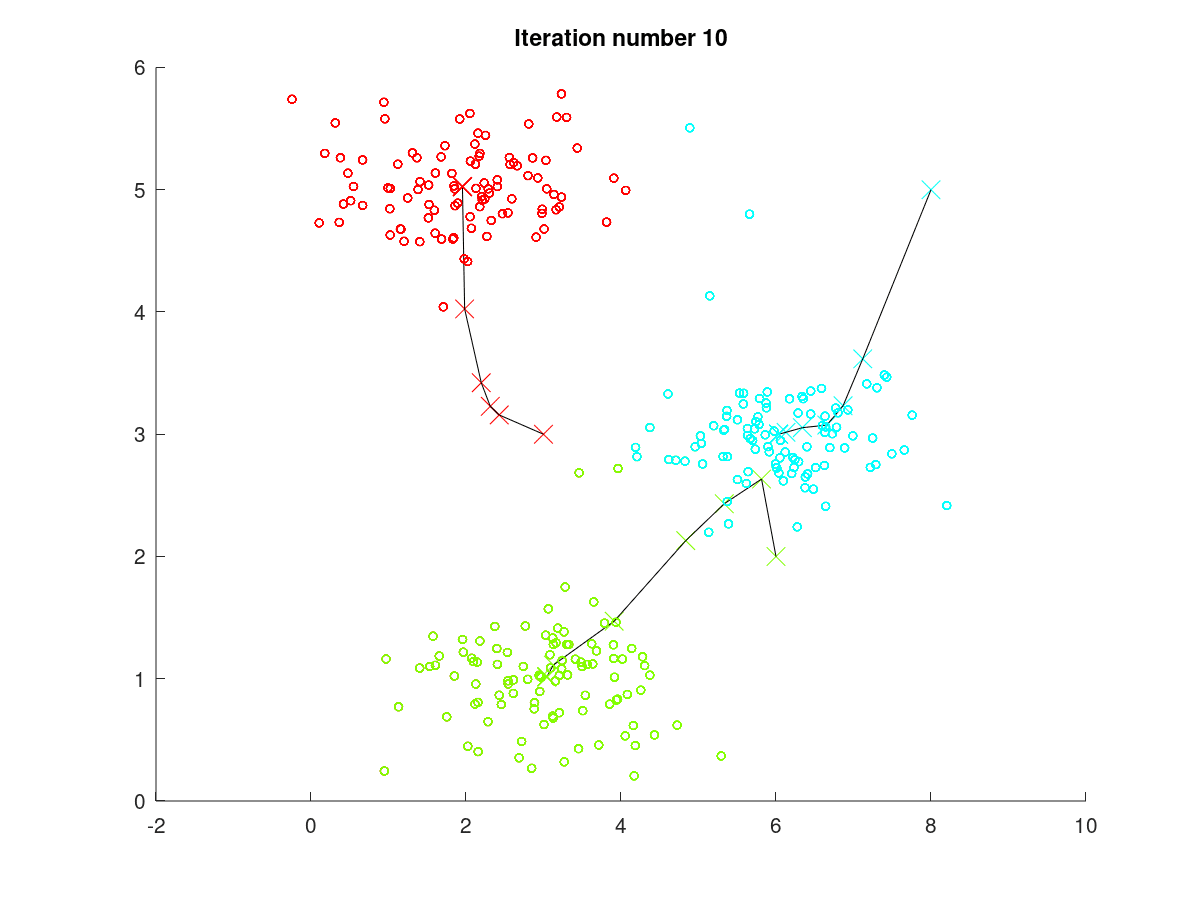
按照上述介绍的步骤,在K-means方法中,图1至图2的迭代过程的可视化展现效果如下图4。下图折线显示了随着聚类过程进行,聚类质心的移动情况,可见,在迭代至第6次(Iteration number 6)左右时,聚类质心位置不再变动,聚类结果保持稳定。
图4 K-means训练过程
K-means的分类效果
下面,我们来看一下,如何通过K-means方法相对客观公正地判断出王小明同学属于哪一类学生。
我们现在已经收集到王小明班级15名同学的数学和英语成绩(如下表所示)。现在我们要做的就是,以此为依据,将班上的学生分成三档:优秀、中等、须努力(即,指定三个簇)。需要注意的是,根据K-means算法,每一个档次的学生并不一定是5个人。
| 学生姓名 | 数学成绩 | 英语成绩 |
|---|---|---|
| 王小明 | 62 | 65 |
| 李小天 | 40 | 89 |
| 方兰兰 | 70 | 70 |
| 赵汤圆 | 88 | 92 |
| 程小雪 | 95 | 95 |
| 周超超 | 75 | 72 |
| 徐小红 | 33 | 36 |
| 谭小强 | 44 | 42 |
| 魏大帅 | 60 | 69 |
| 郑小成 | 88 | 89 |
| 韩阿龟 | 57 | 75 |
| 杨聪明 | 66 | 88 |
| 白海洋 | 81 | 83 |
| 葛小平 | 95 | 96 |
| 宋大山 | 20 | 21 |
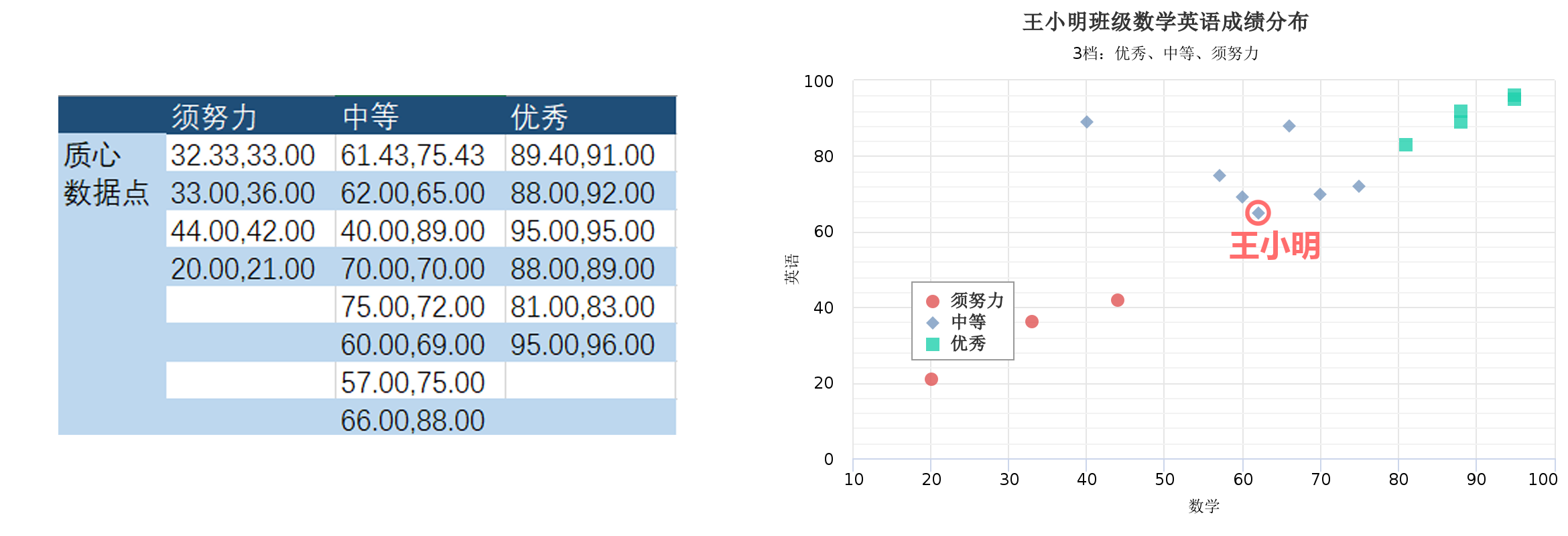
随机选择初始的质心(质心的坐标分别表示类内样本两门课程的平均成绩),多次迭代,直至结果不再变化时,可以认为结果收敛,即当前的结果即为结论。用python实现3,结果如下图5:
图5 王小明班级学生按三档划分
于是我们可以看到,小明同学赶上了中等水平的末班车,可以收获一次表扬了!
继续思考这个问题,如果将全班同学按照数学和英语成绩分成:优、良、中、合格,须努力这五个水平,按照达到中等水平就可以被表扬的标准,那么小明同学会收获表扬吗?
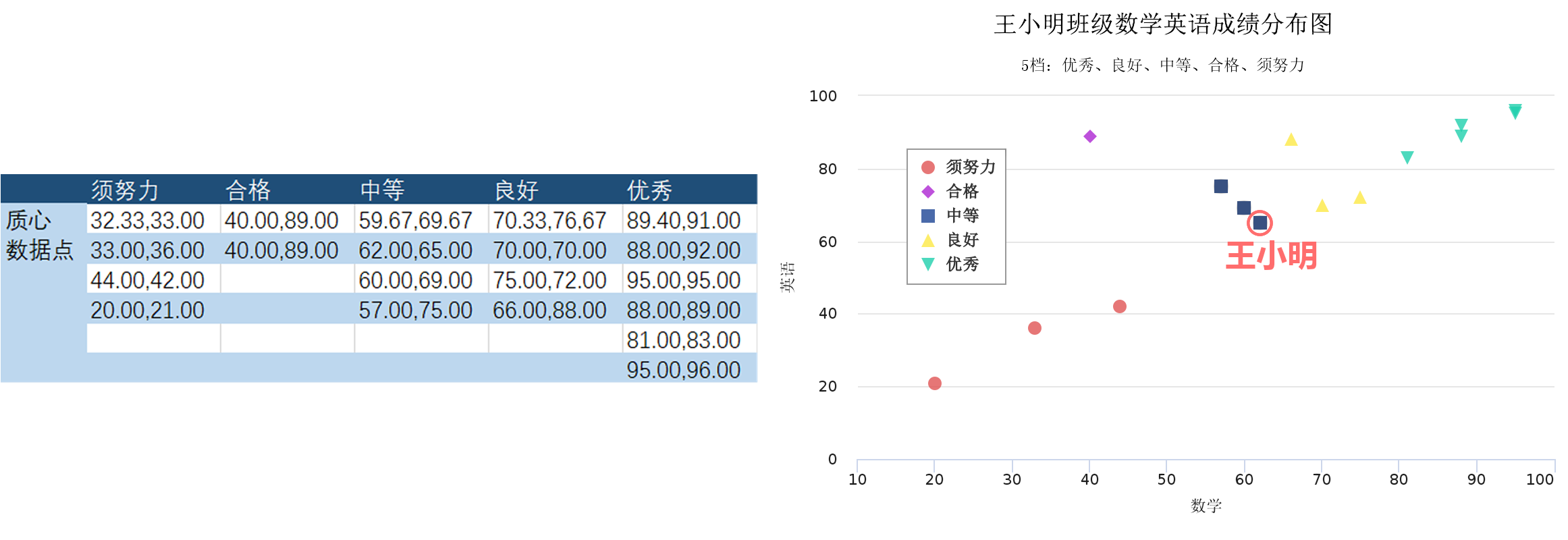
在解决这个问题时,只需要将簇的个数由3改为5,就是将全班同学分成五档的问题了,结果如下图6:
图6 王小明班级学生按五档划分
我们的小明同学简直就是天选之子,再一次赶上了末班车,成功获得了被爸爸表扬的机会!
现在问题继续复杂化:究竟是分成三档还是五档合理呢?其实,我们并不知道需要把小明班的学生分成几档,但是我们仍希望将他们合理地区分。小明班只有15个学生,我们完全可以枚举法,将2类到15类逐个枚举一番。不过如果小明班上有150个学生,这就不是一个好方法了。下面介绍两种能帮助我们确定一个合适的 K K K值的方法:轮廓系数法与肘部确定法。
轮廓系数(Silhouette Coefficient)
轮廓系数是用于评价聚类效果好坏的一种指标,包含有两种因素——内聚度和分离度4。内聚度可以理解为反映一个样本点与类内元素的紧密程度。分离度可以理解为反映一个样本点与类外元素的紧密程度。
轮廓系数 S S S的公式如下:
S = b − a m a x { a , b } S = \frac{b-a}{max\{a, b\}} S=max{
a,b}b−a
其中, a a a是样本点到它所属的簇中所有其他样本点的平均距离。 b b b是样本点与下一个最近簇中所有点的平均距离。
化简公式,可得:
S = { 1 − a b a < b 0 a = b a b − 1 a > b S =\begin{cases} 1-\frac{a}{b} & a<b\\ 0 & a=b\\ \frac{a}{b}-1 & a>b \end{cases} S=⎩⎪⎨⎪⎧1−ba0ba−1a<ba=ba>b
轮廓系数 S S S的取值范围为 [ − 1 , 1 ] [-1, 1] [−1,1],越趋近于1代表轮廓越明显,越趋近于-1则聚类的效果越差。我们不难看出:当 a < b a<b a<b时,即类内的距离小于类间距离,则聚类结果更紧凑, S S S的值会趋近于1。相反,当时 a > b a>b a>b,即类内的距离大于类间距离,说明聚类的结果很松散, S S S的值会趋近于-1。
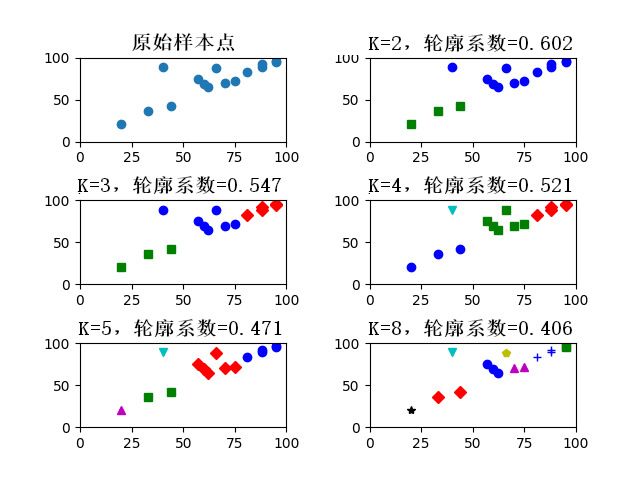
我们可以根据轮廓系数来确定最佳聚类数。 比如,下图7分别说明了簇数增加的聚类情况以及轮廓系数的变化。使用轮廓系数法时,对于王小明的班级来说, K = 2 K=2 K=2 时轮廓系数最大,分类效果最好。
图7 轮廓系数法
肘部确定法(Elbow Method)
K-means以最小化样本与质点的平方误差作为目标函数5,将每个簇的质点与簇内样本点的平方距离误差和称为畸变程度。那么,对于一个簇,它的畸变程度越低,代表簇内成员越紧密,畸变程度越高,代表簇内结构越松散。 畸变程度会随着类别的增加而降低,但对于有一定区分度的数据,存在着一个临界点,该点之前畸变程度快速下降,该点之后缓慢下降,从图像上看就像手肘的肘关节。这个临界点就可以考虑为聚类性能较好的点。
我们通过SSE(和方差) 来衡量这种畸变程度(若要深入了解和方差,请参考机器学习的评价指标6)。设有多个簇 C = { C 1 , C 2 , C 3 , ⋯ , C k } C=\{C_1,C_2,C_3,\cdots,C_k\} C={
C1,C2,C3,⋯,Ck}, μ ( i ) \mu^{(i)} μ(i)是第 i i i个簇的中心,则有:
S S E = ∑ i = 1 K ∑ x ∈ C i ∣ x − μ ( i ) ∣ 2 SSE=\sum\limits_{i=1}^{K}\sum\limits_{x\in{C_i}}{|x-\mu^{(i)}|^2} SSE=i=1∑Kx∈Ci∑∣x−μ(i)∣2
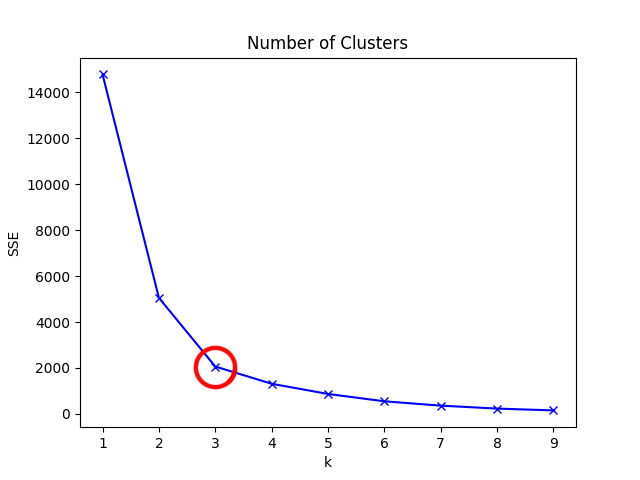
下图8绘制了 K K K值与SSE的关系图7,从图上我们容易看出,在 K = 3 K=3 K=3时,畸变程度发生显著变化,因此我们可以将 K = 3 K=3 K=3选为合适的簇数。
图8 肘部确定法
需要注意的是,以上这两种方法只是帮助我们挑选了该方法下最合适的 K K K值,但是实际应用中,我们需要结合实际情况和需求来确定我们想要的 K K K值。最大轮廓系数对应的 K K K值,并不一定是正确的聚类结果;肘部确定法也不是在所有的情况下,都能绘制出图8那样有明显拐点的曲线。就像上述两种方法给出的 K K K不是同一个值一样,方法只是帮助我们进行判断,但不是我们选择的唯一依据。
改进K-means之K-means++
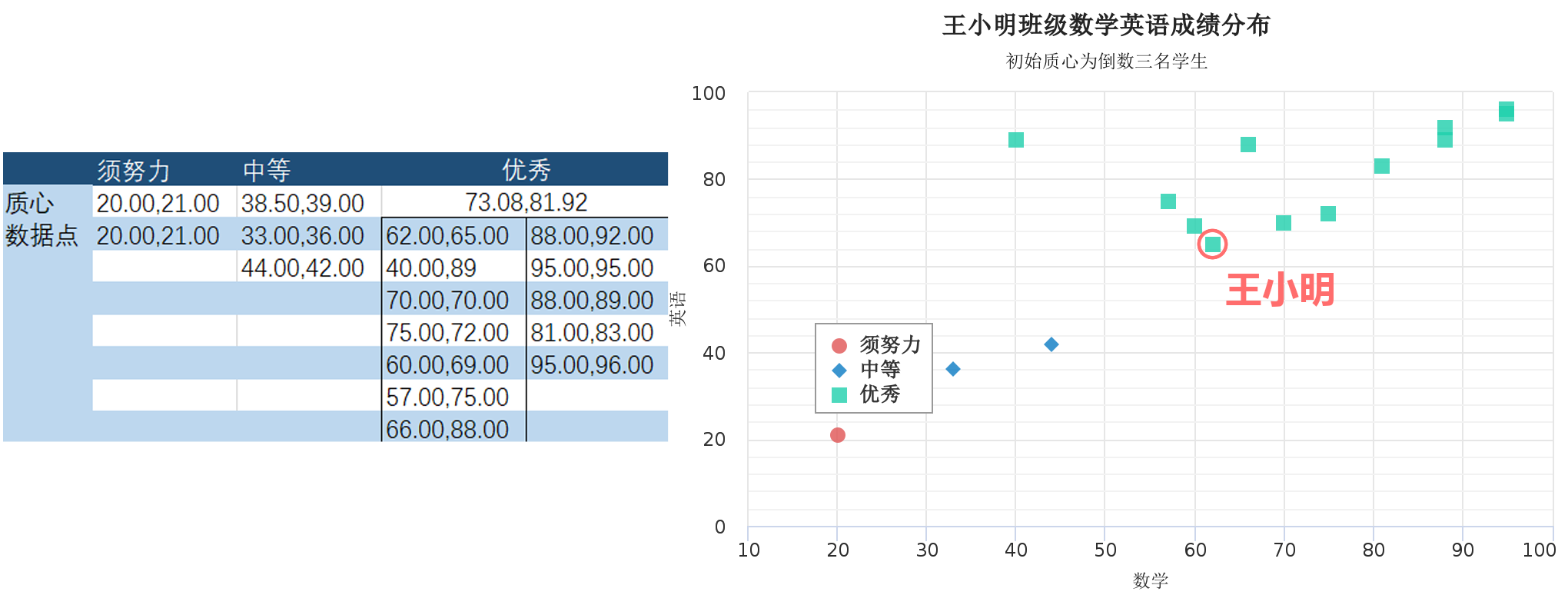
K-means需要人为地在一开始指定聚类质心,初始的质心若寻找的不够恰当,则会影响最后的结果。在前面的例子中如果我们把三个初始质心选择为宋大山、徐小红和谭小强这三个成绩倒数的同学,得到的聚类结果如下图9所示。学习水平较差的学生被分进了两个簇,而中下水平到优秀的学生全部被分进了一个簇,显然这不是一个合适的选择。我们得到的聚类结果,其参考价值较弱。
K-means++算法选择初始的质心的基本思想就是:初始的质心之间的相互距离要尽可能的远。
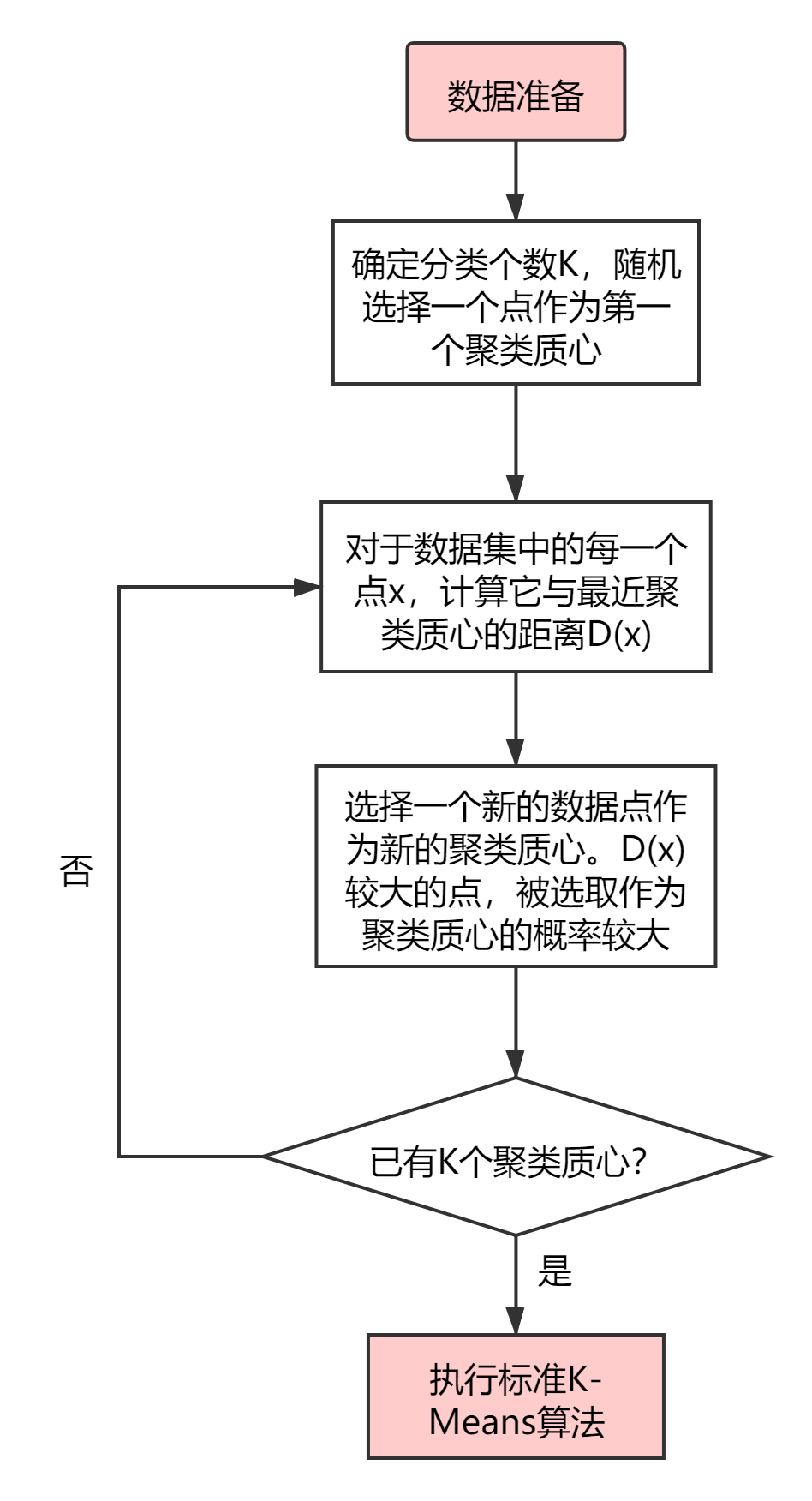
K-means++ 选择初始质心的步骤详见下图10所示。
图10 K-means++流程图
什么是KNN(K-nearest neighbors)
KNN算法,是一种常用的分类算法,其与K-means都使用了邻近算法思想(给定一个点,在数据集中找离它最近的点),二者经常容易被混淆。
该算法的思想是:一个样本与数据集中的 K K K 个样本最相似,如果这 K K K 个样本中的大多数属于某一个类别,则该样本也属于这个类别。使用KNN算法时,我们只依据待判断样本点周边样本的类别,来决定这个未知类别的样本属于什么类。
KNN算法的中心思想是,近朱者赤近墨者黑,即如果你周围的都是好人,则你估计也是好人!
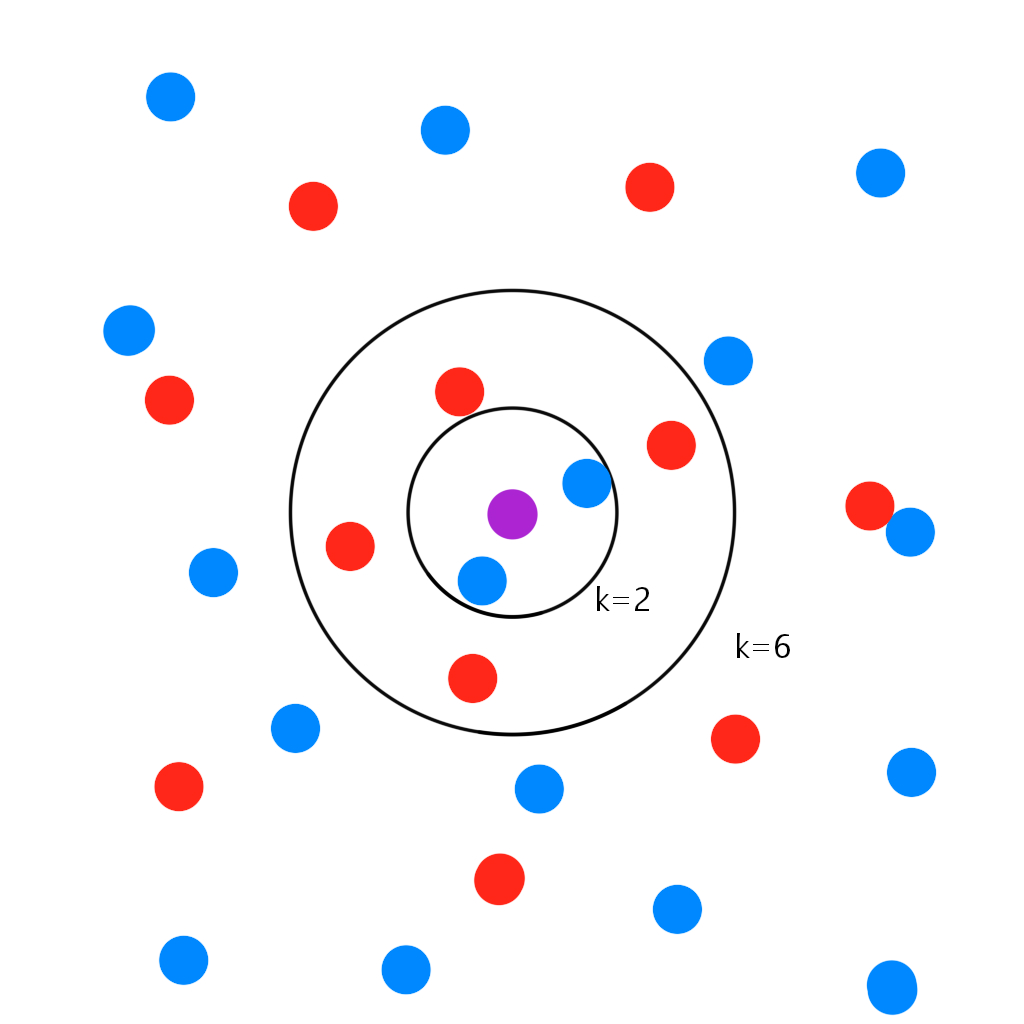
我们以一个例子来说明,从下图11中我们可以看到,图中的数据样本点都被打好了标签,一类是蓝色的圆圈,一类是红色的圆圈。而紫色的圆圈是需要被分类的待判断样本点。 如果 K = 2 K=2 K=2,离紫色圈最近的是两个蓝色圆圈,则紫色圈打上蓝色的标签。 如果 K = 6 K=6 K=6,离紫色圈最近的是两个蓝色圈和四个红色圈,则紫色圈打上红色的标签。
K-means与KNN的比较
| KNN | K-Means |
|---|---|
| 分类算法,输入数据均带有标签 即,有监督学习 |
聚类算法,输入的数据没有标签 即,无监督学习 |
| K代表K个最邻近的点 | K代表K个类别 |
| 没有明显的前期训练过程 | 有明显的前期训练过程 |
共同点:都用到了邻近算法。
小结
- K-means是一种无监督学习的聚类算法,可以在有若干没有分类的数据的情况下,将它们自动地归为K个类别。每一个类别称为一个簇。
- 相同簇中的数据相似度较高,不同簇中数据相似度较低。
- 各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
- K K K的值既可以是我们自己设定的,也可以通过运用轮廓系数法或肘部确定法自动选出。
- 有大量无序数据时,就可以使用K-means将它们自动、合理地分为 K K K个类别。
- K-means原理简单、速度快,对大数据集有比较好的伸缩性;但同时需要指定聚类数量 K K K,对异常值和初始值敏感。K-means++算法可以克服对初始值敏感的缺点,达到更好的聚类效果。
- KNN是一种有监督学习的分类算法,可以在已有部分已分类的数据的情况下,根据未知类别数据周围 K K K 个样本的大多数类别,来判定未知数据的类别。
参考文献
今天的文章机器学习初探:(十)K均值聚类(K-means)以及KNN算法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/65809.html