一维Burgers方程的学习——来自流沙公众号

伯格斯方程(Burgers equation) 是一个模拟冲击波的传播和反射的非线性偏微分方程。
伯格斯方程也称为粘性伯格斯方程，只适用于一个空间维度。

由于编程需要用到sympy，故先对sympy进行简单认识，学习了4个功能：
solve，integere，limit，diff，dsolve
以及对**Symbol()**的认识：在sympy里未知数变量需要做一个额外的定义，用作符号运算。

from sympy import *

# 1、解普通方程
x = Symbol('x')  # 在sympy里未知数变量需要做一个额外的定义：x=symbols（'x'）      符号运算
y = Symbol('y')
print (solve([2*x+3*y-3,5*x+6*y-1],[x,y]))

# 2、解微积分
n = Symbol('n')
s = ((n+2)/(n+1))**3
print(limit(s,n,oo))   #无穷为两个小写oo

# 3、求定积分
t = Symbol('t')
x = Symbol('x')
m = integrate(sin(t)/(pi-t),(t,0,x))
n = integrate(m,(x,0,pi))
print(n)

# 4、解微分方程
f = Function('f')
x = Symbol('x')
print (dsolve(diff(f(x),x) - 2*f(x)*x,f(x)))   # diff(f(x),x，n)表示求解n阶导

有了这个认识再对Burgers方程进行编程学习
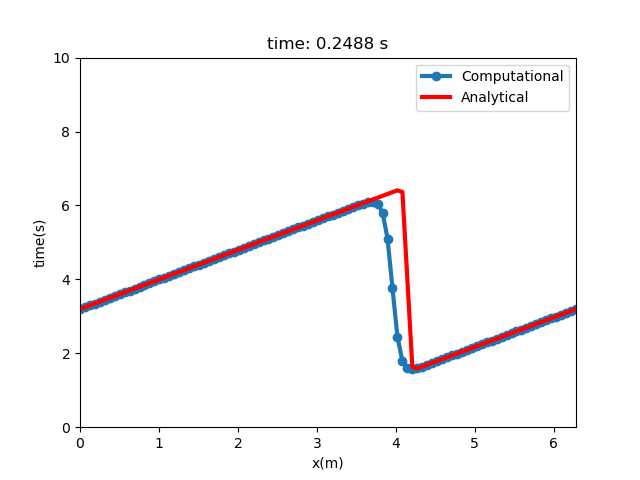
对于初值采用了解析解中t=0的值，
最后计算值也与解析解进行了对比，误差很大。

import numpy as np
import sympy
from sympy.utilities.lambdify import lambdify
from matplotlib import pyplot as plt

x = sympy.Symbol('x')
nu = sympy.Symbol('nu')
t = sympy.Symbol('t')
# 定义phi的表达式
phi = sympy.exp(-(x - 4 * t)**2 / (4 * nu * (t + 1))) + \
      sympy.exp(-(x - 4 * t - 2 * sympy.pi)**2 / (4 * nu * (t + 1)))
# 计算phi偏导数
phiprime = sympy.diff(phi,x)

# 得到u的表达式
u = -2 * nu / phi * phiprime + 4
# 定义lambdify函数，将其携程python可计算的形式
ufunc = lambdify((t,x,nu),u)

# 定义初始条件
nx = 101 # 网格数量
nt = 100 # 时间步数
dx = 2 * np.pi / (nx -1) # 网格尺寸
nu = 0.04 # 粘性系数
dt = dx * nu # 时间步长，为了满足CFL条件

x = np.linspace(0,2*np.pi,nx)
un = np.empty(nx)
t = 0
u = np.asarray([ufunc(t, x0, nu) for x0 in x]) # 定义初始速度

u_analytical = np.asarray([ufunc(nt * dt, xi, nu) for xi in x])  # 准确值 

plt.ion() # 开启了交互模式，打开交互模式 ,同时打开两个窗口显示图片

for n in range(nt):
	plt.cla()
	un = u.copy()
	for i in range(1,nx-1):
		u[i] = un[i] - un[i] * dt / dx * (un[i] - un[i-1]) + nu * dt / dx**2 * (un[i+1] - 2*un[i] + un[i-1])
	u[0] = un[0] - un[0] * dt / dx * (un[0] - un[-2]) + nu * dt / dx**2 * (un[1] - 2*un[0] + un[-2])     # 计算第一个点
	u[-1] = u[0]  # 第一个点和最后一个点相等
	plt.plot(x,u,marker='o',lw=3,label='Computational')
	plt.plot(x,u_analytical,lw=3,label='Analytical',color='red')
	plt.xlim([0,2*np.pi])
	plt.ylim([0,10])
	plt.xlabel("x(m)")
	plt.ylabel("time(s)")
	plt.legend()    # 图例
	plt.title("time: %.4f s"% (n*dt)) # 将时间打印到图形
	plt.pause(0.2)  # 控制图形显示时间

plt.ioff()
plt.show()