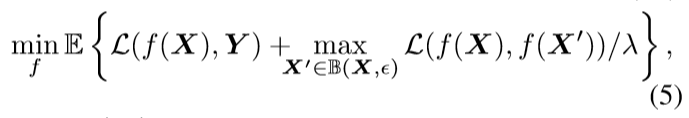Theoretically Principled Trade-off between Robustness and Accuracy

Zhang H, Yu Y, Jiao J, et al. Theoretically Principled Trade-off between Robustness and Accuracy[J]. arXiv: Learning, 2019.

@article{zhang2019theoretically,
title={Theoretically Principled Trade-off between Robustness and Accuracy},
author={Zhang, Hongyang and Yu, Yaodong and Jiao, Jiantao and Xing, Eric P and Ghaoui, Laurent El and Jordan, Michael I},
journal={arXiv: Learning},
year={2019}}

概

从二分类问题入手, 拆分${\mathcal{R}}_{rob}$为${\mathcal{R}}_{nat},{\mathcal{R}}_{bdy}$, 通过${\mathcal{R}}_{rob}-{\mathcal{R}}_{nat}^{\ast }$的上界建立损失函数，并将这种思想推广到一般的多分类问题.

主要内容

符号说明

$X,Y$: 随机变量;
$x\in \mathcal{X},y$: 样本, 对应的标签($1,-1$);
$f$: 分类器(如神经网络);
$\mathbb{B}(x,ϵ)$: { x ′ ∈ X : ∥ x ′ − x ∥ ≤ ϵ } \{x’\in \mathcal{X}:\|x’-x\| \le \epsilon\} {
x′∈X:∥x′−x∥≤ϵ};
$\mathbb{B}(DB(f),ϵ)$: { x ∈ X : ∃ x ′ ∈ B ( x , ϵ ) , s . t .   f ( x ) f ( x ′ ) ≤ 0 } \{x \in \mathcal{X}: \exist x’\in \mathbb{B}(x,\epsilon), \mathrm{s.t.} \: f(x)f(x’)\le0\} {
x∈X:∃x′∈B(x,ϵ),s.t.f(x)f(x′)≤0} ;
${\psi }^{\ast }(u)$: sup ⁡ u { u T v − ψ ( u ) } \sup_u\{u^Tv-\psi(u)\} supu​{
uTv−ψ(u)}, 共轭函数;
$\varphi$: surrogate loss.

Error

R r o b ( f ) : = E ( X , Y ) ∼ D 1 { ∃ X ′ ∈ B ( X , ϵ ) , s . t .   f ( X ′ ) Y ≤ 0 } , (e.1) \tag{e.1} \mathcal{R}_{rob}(f):= \mathbb{E}_{(X,Y)\sim \mathcal{D}}\mathbf{1}\{\exist X’ \in \mathbb{B}(X, \epsilon), \mathrm{s.t.} \: f(X’)Y \le 0\}, Rrob​(f):=E(X,Y)∼D​1{
∃X′∈B(X,ϵ),s.t.f(X′)Y≤0},(e.1)
其中$1(\cdot )$表示指示函数, 显然${\mathcal{R}}_{rob}(f)$是关于分类器$f$存在adversarial samples 的样本的点的测度.

R n a t ( f ) : = E ( X , Y ) ∼ D 1 { f ( X ) Y ≤ 0 } , (e.2) \tag{e.2} \mathcal{R}_{nat}(f) :=\mathbb{E}_{(X,Y)\sim \mathcal{D}}\mathbf{1}\{f(X)Y \le 0\}, Rnat​(f):=E(X,Y)∼D​1{
f(X)Y≤0},(e.2)
显然${\mathcal{R}}_{nat}(f)$是$f$正确分类真实样本的概率, 并且${\mathcal{R}}_{rob}\ge {\mathcal{R}}_{nat}$.

R b d y ( f ) : = E ( X , Y ) ∼ D 1 { X ∈ B ( D B ( f ) , ϵ ) ,   f ( X ) Y > 0 } , (e.3) \tag{e.3} \mathcal{R}_{bdy}(f) :=\mathbb{E}_{(X,Y)\sim \mathcal{D}}\mathbf{1}\{X \in \mathbb{B}(DB(f), \epsilon), \:f(X)Y > 0\}, Rbdy​(f):=E(X,Y)∼D​1{
X∈B(DB(f),ϵ),f(X)Y>0},(e.3)
显然
$${\mathcal{R}}_{rob}-{\mathcal{R}}_{nat}={\mathcal{R}}_{bdy}.\text{\hspace{1em}(1)}$$

因为想要最优化$0-1$loss是很困难的, 我们往往用替代的loss $\varphi$, 定义:
$$\begin{gathered} {\mathcal{R}}_{\varphi }(f):={\mathbb{E}}_{(X,Y)\sim \mathcal{D}}\varphi (f(X)Y), \\ {\mathcal{R}}_{\varphi }^{\ast }(f):=\underset{f}{\min }{\mathcal{R}}_{\varphi }(f). \end{gathered}$$

Classification-calibrated surrogate loss

这部分很重要, 但是篇幅很少, 我看懂, 等回看了引用的论文再讨论.

引理2.1

定理3.1

在假设1的条件下$\varphi (0)\ge 1$, 任意的可测函数$f:\mathcal{X}\to \mathbb{R}$, 任意的于 X × { ± 1 } \mathcal{X}\times \{\pm 1\} X×{
±1}上的概率分布, 任意的$\lambda >0$, 有
$$\begin{array}{ll}& {\mathcal{R}}_{rob}(f)-{\mathcal{R}}_{nat}^{\ast }\\ \le & {\psi }^{-1}({\mathcal{R}}_{\varphi }(f)-{\mathcal{R}}_{\varphi }^{\ast })+\mathbf{P}\mathbf{r}[X\in \mathbb{B}(DB(f),ϵ),f(X)Y>0]\\ \le & {\psi }^{-1}({\mathcal{R}}_{\varphi }(f)-{\mathcal{R}}_{\varphi }^{\ast })+\mathbb{E}{\max }_{X^{\prime }\in \mathbb{B}(X,ϵ)}\varphi (f(X^{\prime })f(X)/\lambda ).\end{array}$$
最后一个不等式, 我知道是因为$\varphi (f(X^{\prime })f(X)/\lambda )\ge 1.$

定理3.2

结合定理$3.1,3.2$可知, 这个界是紧的.

由此导出的TRADES算法

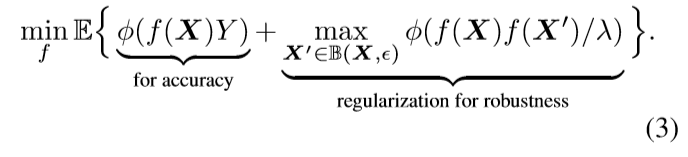
二分类问题, 最优化上界, 即:

扩展到多分类问题, 只需:

算法如下:

实验概述

5.1: 衡量该算法下, 理论上界的大小差距;
5.2: MNIST, CIFAR10 上衡量$\lambda$的作用, $\lambda$越大${\mathcal{R}}_{nat}$越小, ${\mathcal{R}}_{rob}$越大, CIFAR10上反映比较明显;
5.3: 在不同adversarial attacks 下不同算法的比较;
5.4: NIPS 2018 Adversarial Vision Challenge.

代码

import torch
import torch.nn as nn





def quireone(func): #a decorator, for easy to define optimizer
    def wrapper1(*args, **kwargs):
        def wrapper2(arg):
            result = func(arg, *args, **kwargs)
            return result
        wrapper2.__doc__ = func.__doc__
        wrapper2.__name__ = func.__name__
        return wrapper2
    return wrapper1


class AdvTrain:

    def __init__(self, eta, k, lam,
                 net, lr = 0.01, **kwargs):
        """ :param eta: step size for adversarial attacks :param lr: learning rate :param k: number of iterations K in inner optimization :param lam: lambda :param net: network :param kwargs: other configs for optim """
        kwargs.update({ 
   'lr':lr})
        self.net = net
        self.criterion = nn.CrossEntropyLoss()
        self.opti = self.optim(self.net.parameters(), **kwargs)
        self.eta = eta
        self.k = k
        self.lam = lam

    @quireone
    def optim(self, parameters, **kwargs):
        """ quireone is decorator defined below :param parameters: net.parameteres() :param kwargs: other configs :return: """
        return torch.optim.SGD(parameters, **kwargs)


    def normal_perturb(self, x, sigma=1.):

        return x + sigma * torch.randn_like(x)

    @staticmethod
    def calc_jacobian(loss, inp):
        jacobian = torch.autograd.grad(loss, inp, retain_graph=True)[0]
        return jacobian

    @staticmethod
    def sgn(matrix):
        return torch.sign(matrix)

    def pgd(self, inp, y, perturb):
        boundary_low = inp - perturb
        boundary_up = inp + perturb
        inp.requires_grad_(True)
        out = self.net(inp)
        loss = self.criterion(out, y)
        delta = self.sgn(self.calc_jacobian(loss, inp)) * self.eta
        inp_new = inp.data
        for i in range(self.k):
            inp_new = torch.clamp(
                inp_new + delta,
                boundary_low,
                boundary_up
            )
        return inp_new

    def ipgd(self, inps, ys, perturb):
        N = len(inps)
        adversarial_samples = []
        for i in range(N):
            inp_new = self.pgd(
                inps[[i]], ys[[i]],
                perturb
            )
            adversarial_samples.append(inp_new)

        return torch.cat(adversarial_samples)

    def train(self, trainloader, epoches=50, perturb=1, normal=1):

        for epoch in range(epoches):
            running_loss = 0.
            for i, data in enumerate(trainloader, 1):
                inps, labels = data

                adv_inps = self.ipgd(self.normal_perturb(inps, normal),
                                     labels, perturb)

                out1 = self.net(inps)
                out2 = self.net(adv_inps)

                loss1 = self.criterion(out1, labels)
                loss2 = self.criterion(out2, labels)

                loss = loss1 + loss2

                self.opti.zero_grad()
                loss.backward()
                self.opti.step()
                
                running_loss += loss.item()

                if i % 10 is 0:
                    strings = "epoch {0:<3} part {1:<5} loss: {2:<.7f}\n".format(
                        epoch, i, running_loss
                    )
                    print(strings)
                    running_loss = 0.

今天的文章Theoretically Principled Trade-off between Robustness and Accuracy分享到此就结束了，感谢您的阅读。