FDU邱锡鹏《神经网络与深度学习》第 2 章机器学习概述及习题全解

本篇为对机器学习基础的概要总结。内容来源: 《神经网络与深度学习》。

通俗地讲，机器学习（Machine Learning， ML）就是让计算机从数据中进行自动学习，得到某种知识（或规律）。作为一门学科，机器学习通常指一类问题以及解决这类问题的方法，即如何从观测数据（样本）中寻找规律，并利用学习到的规律（模型）对未知或无法观测的数据进行预测。

机器学习问题在早期的工程领域也经常称为模式识别（Pattern Recognition， PR），但模式识别更偏向于具体的应用任务，比如光学字符识别、语音识别，人脸识别等。这些任务的特点是对于我们人类而言，这些任务很容易完成，但我们不知道自己是如何做到的，因此也很难人工设计一个计算机程序来解决这些任务。一个可行的方法是设计一个算法可以让计算机自己从有标注的样本上学习其中的规律，并用来完成各种识别任务。随着机器学习技术的应用越来越广，现在机器学习的概念逐渐替代模式识别，成为这一类问题及其解决方法的统称。
本章先介绍机器学习的基本概念和要素，并较详细地描述一个简单的机器学习例子， 线性回归。

2.1 基本概念

首先介绍下机器学习中的一些基本概念：包括样本、特征、标签、模型、学习算法等。以一个生活中的经验学习为例，假设我们要到市场上购买芒果，但是之前毫无挑选芒果的经验，那么我们如何通过学习来获取这些知识？

首先，我们从市场上随机选取一些芒果，列出每个芒果的特征（Feature）特征也可以称为属性（Attribute）。，包括颜色，大小，形状，产地，品牌，以及我们需要预测的标签（label）。标签可以连续值（比如关于芒果的甜度、水分以及成熟度的综合打分），也可以是离散值（比如“好”“坏”两类标签）。样本（Sample），也叫示例（Instance）。

一个标记好特征以及标签的芒果可以看作是一个样本（Sample）。一组样本构成的集合称为数据集（Data Set）。一般将数据集分为两部分：训练集和测试集。训练集（Training Set）中的样本是用来训练模型的，也叫训练样本（Training Sample），而测试集（Test Set）中的样本是用来检验模型好坏的，也叫测试样本（Test Sample）。在很多领域，数据集也经常称为语料库（Corpus）。

我们用一个 d维向量 $\mathbf{x}=\left[x_{1}, x_{2}, \cdots, x_{d}\right]^{\mathrm{T}}$ 表示一个芒果的所有特征构成的向量，称为特征向量（Feature Vector），其中每一维表示一个特征。假设训练集由 N 个样本组成，其中每个样本都是独立同分布（Identically and Independently Distributed， IID）的，即独立地从相同的数据分布中抽取的，即为：

$\mathcal{D}=\left\{\left(\mathbf{x}^{(1)}, y^{(1)}\right),\left(\mathbf{x}^{(2)}, y^{(2)}\right), \cdots,\left(\mathbf{x}^{(N)}, y^{(N)}\right)\right\}$

并不是所有的样本特征都是数值型，需要通过转换表示为特征向量，参见第2.6节。

给定训练集D，我们希望让计算机自动寻找一个函数 f(x, θ)来建立每个样本特性向量x和标签y 之间的映射。对于一个样本x，我们可以通过决策函数来预测其标签的值

$\hat{y}=f(\mathbf{x}, \theta)$

或标签的条件概率

$p(y | \mathbf{x})=f_{y}(\mathbf{x}, \theta)$

其中 θ 为可学习的参数。

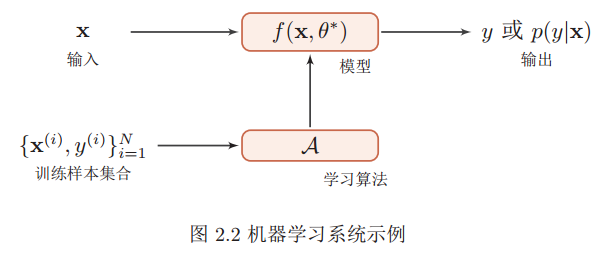
图2.2给出了机器学习的基本概念。对一个预测任务，输入特征向量为x，输方法。出标签为y，我们选择一个函数f(x, θ)，通过学习算法A和一组训练样本D，找到一组最优的参数θ∗，得到最终的模型f(x, θ∗)。这样就可以对新的输入x进行预测。

2.2 机器学习的三个基本要素

机器学习是从有限的观测数据中学习（或“猜测”）出具有一般性的规律，并可以将总结出来的规律推广应用到未观测样本上。机器学习方法可以粗略地分为三个基本要素：模型、学习准则、优化算法。

2.2.1 模型

一个机器学习任务要先需要确定其输入空间 X 和输出空间 Y。不同机器学习任务的主要区别在于输出空间不同。在两类分类问题中 $\mathcal{Y}=\{+1,-1\}$ ，在 C类分类问题中 $\mathcal{Y}=\{1,2, \cdots, C\}$ ，而在回归问题中 Y = R。这里，

输入空间默认为样本输入空间 $\mathcal{X}$ 和输出空间 $\mathcal{Y}$ 构成了一个样本空间。对于样本空间中的样本 $(\mathbf{x}, y) \in \mathcal{X} \times \mathcal{Y}$ ，假定存在一个未知的真实映射函数 $g : \mathcal{X} \rightarrow \mathcal{Y}$ 使得

$y=g(\mathbf{x})$

或者真实条件概率分布

$p_{r}(y | \mathbf{x})$

机器学习的目标是找到一个模型来近似真实映射函数 $g(\mathbf{x})$ 或真实条件概率分布 $p_{r}(y | \mathbf{x})$ 。

2.2.1.1 线性模型

线性模型的假设空间为一个参数化的线性函数族，对于分类问题，一般为广义线性函数，参见公式 (3.3)。

$f(\mathbf{x}, \theta)=\mathbf{w}^{\mathrm{T}} \mathbf{x}+b$
其中参数 θ 包含了权重向量 w和偏置 b。

2.2.1.2 非线性模型

广义的非线性模型可以写为多个非线性基函数 ϕ(x)的线性组合

$f(\mathbf{x}, \theta)=\mathbf{w}^{\mathrm{T}} \boldsymbol{\phi}(\mathbf{x})+b$

$\phi(\mathbf{x})=\left[\phi_{1}(\mathbf{x}), \phi_{2}(\mathbf{x}), \cdots, \phi_{K}(\mathbf{x})\right]^{\mathrm{T}}$ 为K 个非线性基函数组成的向量，参数 θ 包含了权重向量 w和偏置 b。

如果 ϕ(x)本身为可学习的基函数，比如

$\phi_{k}(\mathbf{x})=h\left(\mathbf{w}_{k}^{\mathrm{T}} \boldsymbol{\phi}^{\prime}(\mathbf{x})+b_{k}\right), \forall 1 \leq k \leq K$

其中 $h(\cdot)$ 为非线性函数， $\phi^{\prime}(\mathbf{x})$ 为另一组基函数， w_k 和 b_k 为可学习的参数，则 $f(\mathbf{x}, \theta)$ 就等价于神经网络模型。

2.2.2 学习准则

好的模型应该与真实映射函数一致或者与真实条件概率一致。

2.2.2.1 损失函数

2.2.2.2 风险最小化准则

2.2.3 优化算法

在确定了训练集 D、假设空间 F 以及学习准则后，如何找到最优的模型f(x, θ∗)就成了一个最优化（Optimization）问题。机器学习的训练过程其实就是最优化问题的求解过程。

参数与超参数 常见的超参数包括：聚类算法中的类别个数、梯度下降法的步长、正则项的系数、神经网络的层数、支持向量机中的核函数等。超参数的选取一般都是组合优化问题，很难通过优化算法来自动学习。因此，超参数优化是机器学习的一个经验性很强的技术，通常是按照人的经验设定，或者通过搜索的方法对一组超参数组合进行不断试错调整。超参数的优化参见第7.6

2.2.3.1 梯度下降法
为了充分利用凸优化中一些高效、成熟的优化方法，比如共轭梯度、拟牛顿法等，很多机器学习方法都倾向于选择合适的模型和损失函数以构造一个凸函数作为优化目标。但也有很多模型（比如神经网络）的优化目标是非凸的，只能退而求其次找到局部最优解。
不同机器学习算法的区别在于模型、学习准则（损失函数）和优化算法的差异。相同的模型也可以有不同的学习算法。比如线性分类模型有感知器、 logistic回归和支持向量机，它们之间的差异在于使用了不同的学习准则和优化算法。在机器学习中，最简单、常用的优化算法就是梯度下降法，即通过迭代的梯度下降法参见方法来计算训练集D上风险函数的最小值。

2.2.3.2 提前停止

针对梯度下降的优化算法，除了加正则化项之外，还可以通过提前停止来防止过拟合。在梯度下降训练的过程中，由于过拟合的原因，在训练样本上收敛的参数，并不一定在测试集上最优。因此，除了训练集和测试集之外，有时也会使用一个验证集（Validation Set）来进行模型选择，测试模型在验证集上是否最优。在每次迭代时，把新得到的模型 f(x, θ) 在验证集上进行测试，并计算错误率。验证集也叫开发集（Development Set）。如果在验证集上的错误率不再下降，就停止迭代。这种策略叫提前停止（EarlyStop）。如果没有验证集，可以在训练集上划分出一个小比例的子集作为验证集。图2.4给出了提前停止的示例。

2.2.3.3 随机梯度下降法

批量梯度下降和随机梯度下降之间的区别在于每次迭代的优化目标是对所有样本的平均损失函数还是单个样本的损失函数。随机梯度下降因为实现简单，收敛速度也非常快，因此使用非常广泛。随机梯度下降相当于在批量梯度下降的梯度上引入了随机噪声。当目标函数非凸时，反而可以使其逃离局部最优点。

2.2.3.4 Mini-batch

2.3 机器学习的简单示例：线性回归

线性回归（Linear Regression）是机器学习和统计学中最基础和广泛应用的模型，是一种对自变量和因变量之间关系进行建模的回归分析。自变量数量为 1时称为简单回归，自变量数量大于 1时称为多元回归。

2.3.1 参数学习

给定一组包含 N 个训练样本的训练集 $\mathcal{D}=\left\{\left(\mathbf{x}^{(n)}, y^{(n)}\right)\right\}, 1 \leq n \leq N$ ，我们希望能够学习一个最优的线性回归的模型参数 w。

我们介绍四种不同的参数估计方法：经验风险最小化、结构风险最小化、最大似然估计、最大后验估计。

2.3.1.1 经验风险最小化

根据经验风险最小化准则，训练集D 上的的经验风险定义为

$\begin{aligned} \mathcal{R}(\mathbf{w}) &=\sum_{n=1}^{N} \mathcal{L}\left(y^{(n)}, f\left(\mathbf{x}^{(n)}, \mathbf{w}\right)\right) \\ &=\frac{1}{2} \sum_{n=1}^{N}\left(y^{(n)}-\mathbf{w}^{\mathrm{T}} \mathbf{x}^{(n)}\right)^{2} \\ &=\frac{1}{2}\left\|\mathbf{y}-X^{\mathrm{T}} \mathbf{w}\right\|^{2} \end{aligned}$

其中 $\mathbf{y} \in \mathbb{R}^{N}$ 是由每个样本的真实标签 $y^{(1)}, \cdots, y^{(N)}$ 组成的列向量， $X \in \mathbb{R}^{(d+1) \times N}$ 是所有输入 $\mathbf{x}^{(1)}, \cdots, \mathbf{x}^{(N)}\mathbf{x}^{(1)}, \cdots, \mathbf{x}^{(N)}$ 组成的矩阵

$X=\left[ \begin{array}{cccc}{x_{1}^{(1)}} & {x_{1}^{(2)}} & {\dots} & {x_{1}^{(N)}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {x_{d}^{(1)}} & {x_{d}^{(2)}} & {\cdots} & {x_{d}^{(N)}} \\ {1} & {1} & {\cdots} & {1}\end{array}\right]$

风险函数R(w)是关于 w的凸函数，其对 w的偏导数为

$\begin{aligned} \frac{\partial \mathcal{R}(\mathbf{w})}{\partial \mathbf{w}} &=\frac{1}{2} \frac{\partial\left\|\mathbf{y}-X^{\mathrm{T}} \mathbf{w}\right\|^{2}}{\partial \mathbf{w}} \\ &=-X\left(\mathbf{y}-X^{\mathrm{T}} \mathbf{w}\right) \end{aligned}$

令 $\frac{\partial}{\partial \mathbf{w}} \mathcal{R}(\mathbf{w})=0$ ，得到最优的参数 w∗ 为

$\mathbf{w}^{*}=\left(X X^{\mathrm{T}}\right)^{-1} X \mathbf{y}$

$=\left(\sum_{n=1}^{N} \mathbf{x}^{(n)}\left(\mathbf{x}^{(n)}\right)^{\mathrm{T}}\right)^{-1}\left(\sum_{n=1}^{N} \mathbf{x}^{(n)} y^{(n)}\right)$

这种求解线性回归参数的方法也叫最小二乘法估计（Least Square Estimation，LSE）。图2.5给出了用最小二乘法估计方法来进行参数学习的示例。

在最小二乘法估计方法中， $X X^{\mathrm{T}} \in \mathbb{R}^{(d+1) \times(d+1)}$ 必须存在逆矩阵，即 XX T是满秩的 $\left(\operatorname{rank}\left(X X^{\mathrm{T}}\right)=d+1\right)$ 。也就是说， X 中的每一行特征之间是线性不相关的。一种常见的 $X X^{\mathrm{T}}$ 不可逆情况是样本数量 N 小于特征数量(d + 1)， $X X^{\mathrm{T}}$ 的秩为 N。这时会存在很多解 w∗，可以使得 $\mathcal{R}\left(\mathbf{w}^{*}\right)=0$ 。

当 $X X^{\mathrm{T}}$ 不可逆时，可以使用主成分分析等方法来预处理数据，消除不同特征之间的相关性，然后再使用最小二乘估计方法来求解。或者是通过用梯度下降法来求解。初始化 $\mathbf{W}_{0}=0$ ，通过下面公式进行迭代，

$\mathbf{w} \leftarrow \mathbf{w}+\alpha X\left(\mathbf{y}-X^{\mathrm{T}} \mathbf{w}\right)$

其中 α是学习率。这种方法也称为最小均方误差（Least Mean Squares， LMS）算法。

2.3.1.2 结构风险最小化

最小二乘法估计的基本要求是各个特征之间要相互独立，保证 $X X^{\mathrm{T}}$ 可逆。但即使 $X X^{\mathrm{T}}$ 可逆，如果特征之间可能会有较大的共线性（Multicollinearity），也会使得 $X X^{\mathrm{T}}$ 的逆在数值上无法准确计算。数据集 X 上一些小的扰动就会导致 $\left(X X^{\mathrm{T}}\right)^{-1}$ 发生大的改变，进而使得最小二乘法估计的计算变得很不稳定。为了解决这个问题， Hoerl and Kennard [1970]提出了岭回归（Ridge Regression），给 $X X^{\mathrm{T}}$ 的对角线元素都加上一个常数 λ使得 $\left(X X^{\mathrm{T}}+\lambda I\right)$ 满秩，即其行列式不为 0。最优的参数 w∗ 为

$\mathbf{w}^{*}=\left(X X^{\mathrm{T}}+\lambda I\right)^{-1} X \mathbf{y}$

其中 λ > 0为预先设置的超参数， I 为单位矩阵。
岭回归的解 w∗ 可以看做是结构风险最小化准则下的最小二乘法估计。

$\mathcal{R}(\mathbf{w})=\frac{1}{2}\left\|\mathbf{y}-X^{\mathrm{T}} \mathbf{w}\right\|^{2}+\frac{1}{2} \lambda\|\mathbf{w}\|^{2}$

其中 0″>为正则化系数。

2.3.1.3 最大似然估计

机器学习任务可以分为两类，一类是样本的特征向量 x 和标签 y 之间如果存在未知的函数关系 $y=h(\mathrm{x})$ ，另一类是条件概率 $p(y | \mathbf{x})$ 服从某个未知分布。第2.3.1.1中介绍的最小二乘估计是属于第一类，直接建模x和标签y之间的函数关系。此外，线性回归还可以通过建模条件概率 p(y|x)的角度来进行参数估计。

$\begin{aligned} p(y | \mathbf{x}, \mathbf{w}, \sigma) &=\mathcal{N}\left(y | \mathbf{w}^{\mathrm{T}} \mathbf{x}, \sigma^{2}\right) \\ &=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y-\mathbf{w}^{\mathrm{T}} \mathbf{x}\right)^{2}}{2 \sigma^{2}}\right) \end{aligned}$
参数 w在训练集 D 上的似然函数（Likelihood）为

$\begin{aligned} p(\mathbf{y} | X, \mathbf{w}, \sigma) &=\prod_{n=1}^{N} p\left(y^{(n)} | \mathbf{x}^{(n)}, \mathbf{w}, \sigma\right) \\ &=\prod_{n=1}^{N} \mathcal{N}\left(y^{(n)} | \mathbf{w}^{\mathrm{T}} \mathbf{x}^{(n)}, \sigma^{2}\right) \end{aligned}$

为了方便计算，对似然函数取对数得到对数似然函数（Log Likelihood），

$\log p(\mathbf{y} | X, \mathbf{w}, \sigma)=\sum_{n=1}^{N} \log \mathcal{N}\left(y^{(n)} | \mathbf{w}^{\mathrm{T}} \mathbf{x}^{(n)}, \sigma^{2}\right)$

最大似然估计（Maximum Likelihood Estimate， MLE）是指找到一组参数w使得似然函数 $p(\mathbf{y} | X, \mathbf{w}, \sigma)$ 最大，等价于对数似然函数 log $\log p(\mathbf{y} | X, \mathbf{w}, \sigma)$ 最大。

令 $\frac{\partial \log p(\mathbf{y} | X, \mathbf{w}, \sigma)}{\partial \mathbf{w}}=0$ ，得到

$\mathbf{w}^{M L}=\left(X X^{\mathrm{T}}\right)^{-1} X \mathbf{y}$

可以看出，最大似然估计的解和最小二乘估计的解相同。

2.3.1.4 最大后验估计

假设参数 w为一个随机向量，并服从一个先验分布 $p(\mathbf{w} | \nu)$ 。简单起见，一般令 $p(\mathbf{w} | \nu)$ 为各向同性的高斯分布

$p(\mathbf{w} | \nu)=\mathcal{N}\left(\mathbf{w} | \mathbf{0}, \nu^{2} I\right)$

根据贝叶斯公式，那么参数w的后验概率分布（Posterior Distribution）为

$\begin{aligned} p(\mathbf{w} | X, \mathbf{y}, \nu, \sigma) &=\frac{p(\mathbf{w}, \mathbf{y} | X, \nu, \sigma)}{\sum_{\mathbf{w}} p(\mathbf{w}, \mathbf{y} | X, \nu, \sigma)} \\ & \propto p(\mathbf{y} | X, \mathbf{w}, \sigma) p(\mathbf{w} | \nu) \end{aligned}$

令似然函数 $p(\mathbf{y} | X, \mathbf{w}, \sigma)$ )为公式 (2.49)中定义的高斯密度函数，则后验分布 $\log p(\mathbf{y} | X, \mathbf{w}, \sigma)$ 的对数为

$\begin{aligned} \log p(\mathbf{w} | X, \mathbf{y}, \nu, \sigma) & \propto \log p(\mathbf{y} | X, \mathbf{w}, \sigma)+\log p(\mathbf{w} | \nu) \\ & \propto-\frac{1}{2 \sigma^{2}} \sum_{n=1}^{N}\left(y^{(n)}-\mathbf{w}^{\mathrm{T}} \mathbf{x}^{(n)}\right)^{2}-\frac{1}{2 \nu^{2}} \mathbf{w}^{\mathrm{T}} \mathbf{w} \\ &=-\frac{1}{2 \sigma^{2}} \sum^{N}\left\|\mathbf{y}-\mathbf{w}^{\mathrm{T}} X\right\|^{2}-\frac{1}{2 \nu^{2}} \mathbf{w}^{\mathrm{T}} \mathbf{w} \end{aligned}$

2.4 偏差-方差分解

$\begin{aligned} \mathbb{E}_{\mathcal{D}} &\left[\left(f_{\mathcal{D}}(\mathbf{x})-f^{*}(\mathbf{x})\right)^{2}\right] \\ &=\mathbb{E}_{\mathcal{D}}\left[\left(f_{\mathcal{D}}(\mathbf{x})-\mathbb{E}_{\mathcal{D}}\left[f_{\mathcal{D}}(\mathbf{x})\right]+\mathbb{E}_{\mathcal{D}}\left[f_{\mathcal{D}}(\mathbf{x})\right]-f^{*}(\mathbf{x})\right)^{2}\right] \\ &=\underbrace{\left(\mathbb{E}_{\mathcal{D}}\left[f_{\mathcal{D}}(\mathbf{x})\right]-f^{*}(\mathbf{x})\right)^{2}+\mathbb{E}_{\mathcal{D}}\left[\left(f_{\mathcal{D}}(\mathbf{x})-\mathbb{E}_{\mathcal{D}}\left[f_{\mathcal{D}}(\mathbf{x})\right]\right)^{2}\right]} \end{aligned}$

2.5 机器学习算法的类型

监督学习 如果机器学习的目标是通过建模样本的特征 x 和标签 y 之间的关系： $y=f(\mathbf{x}, \theta)$ 或 $p(y | \mathbf{x}, \theta)$ ，并且训练集中每个样本都有标签，那么这类机器学习称为监督学习（Supervised Learning）。根据标签类型的不同，监督学习又可以分为回归和分类两类。
1. 回归（Regression）问题中的标签 y 是连续值（实数或连续整数）， f(x, θ)的输出也是连续值。
2. 分类（Classification）问题中的标签y是离散的类别（符号）。在分类问题中，学习到模型也称为分类器（Classifier）。分类问题根据其类别数量又可分为两类分类（Binary Classification）和多类分类（Multi-class Classification）问题。
3. 结构化学习（Structured Learning）的输出是结构化的对象，比如序列、树或图等。由于结构化学习的输出空间比较大，因此我们一般定义一个联合特征空间，将 x, y 映射为该空间中的联合特征向量 ϕ(x, y)，预测模型可以写为

$\hat{\mathbf{y}}=\underset{\mathbf{y} \in \operatorname{Gen}(\mathbf{x})}{\arg \max } f(\boldsymbol{\phi}(\mathbf{x}, \mathbf{y}), \theta)$

其中 Gen(x)表示输入x所有可能的输出目标集合。计算 arg max的过程也一种基于感知器的结构化学。称为解码（Decoding）过程，一般通过动态规划的方法来计算

无监督学习 无监督学习（Unsupervised Learning， UL）是指从不包含目标标签的训练样本中自动学习到一些有价值的信息。典型的无监督学习问题有聚类、密度估计、特征学习、降维等。无监督学习参见第9章

强化学习 强化学习（Reinforcement Learning， RL）是一类通过交互来学习的机器学习算法。在强化学习中，智能体根据环境的状态做出一个动作，并得到强化学习参见第14章。即时或延时的奖励。智能体在和环境的交互中不断学习并调整策略，以取得最大化的期望总回报。

2.6 数据的特征表示

图像特征 在手写体数字识别任务中，样本 x为待识别的图像。为了识别 x是什么数字，我们可以从图像中抽取一些特征。如果图像是一张大小为 m × n的图像，其特征向量可以简单地表示为 m × n维的向量，每一维的值为图像中对应像素的灰度值。为了提高模型准确率，也会经常加入一个额外的特征，比如直方图、宽高比、笔画数，纹理特征、边缘特征等。假设我们总共抽取了 d 个特征，这些特征可以表示为一个向量 $\mathbf{x} \in \mathbb{R}^{d}$ 。

文本特征 在文本情感分类任务中，样本 x为自然语言文本，类别 y ∈ {+1, -1}分别表示正面或负面的评价。为了将样本x从文本形式转为为向量形式，一种简单的方式是使用词袋模型（Bag-of-Words， BoW）模型。假设训练集合中的词都词袋模型在信息检索中也叫做向量空间模型（Vector Space Model， VSM）来自一个词表V，大小为|V|，则每个样本可以表示为一个|V|维的向量x ∈ R|V|，向量中每一维 xi 的值为词表中的第 i个词是否在 x中出现。如果出现值为 1，否则为 0。

表示学习 如果直接用数据的原始特征来进行预测，对机器学习模型的能力要求比较高。这些原始特征可能存在以下几种不足：（1）特征比较单一，需要进行（非线性的）组合才能发挥其作用；（2）特征之间冗余度比较高；（3）并不是所有的特征都对预测有用；（4）很多特征通常是易变的；（5）特征中往往存在一些噪声。

2.7 评价指标

1. 真正例（True Positive， TP）：一个样本的真实类别为 c并且模型正确地预测为类别 c。这类样本数量记为TP表示。

$T P_{c}=\sum_{n=1}^{N} I\left(y^{(n)}=\hat{y}^{(n)}=c\right)$
2. 假负例（False Negative， FN）：一个样本的真实类别为 c，模型错误地预测为其它类 c。这类样本数量记为

$F N_{c}=\sum_{n=1}^{N} I\left(y^{(n)}=c \wedge \hat{y}^{(n)} \neq c\right)$
3. 假正例（False Positive， FP）一个样本的真实类别为其它类，模型错误地预测为类 c。这类样本数量记为

$F P_{c}=\sum_{n=1}^{N} I\left(y^{(n)} \neq c \wedge \hat{y}^{(n)}=c\right)$
4. 真负例（True Negative， TN）：一个样本的真实类别为其它类，模型也预测为其它类。这类样本数量记为 T Nc。对于类别 c来说，这种情况一般不需要关注。

交叉验证 交叉验证（Cross Validation）是一种比较好的可能衡量机器学习模型的统计分析方法，可以有效避免划分训练集和测试集时的随机性对评价结果造成的影响。我们可以把原始数据集平均分为 K 组不重复的子集，每次选 K – 1组子集作为训练集，剩下的一组子集作为验证集。这样可以进行 K 次试验并得到K 个模型。这K 个模型在各自验证集上的错误率的平均作为分类器的评价。

2.8 理论和定理

2.8.1 PAC 学习理论

机器学习中一个很关键的问题是期望错误和经验错误之间的差异，称为泛化错误（Generalization Error）。泛化错误可以衡量一个机器学习模型 f 是否可以很好地泛化到未知数据。

2.8.2 没有免费午餐定理

没有免费午餐定理（No Free Lunch Theorem， NFL）是由 Wolpert和 Macerday在最优化理论中提出的。没有免费午餐定理证明：对于基于迭代的最优化算法，不存在某种算法对所有问题（有限的搜索空间内）都有效。如果一个算法对某些问题有效，那么它一定在另外一些问题上比纯随机搜索算法更差。也就是说，不能脱离具体问题来谈论算法的优劣，任何算法都有局限性。必须要“具体问题具体分析”。
不存在一种机器学习算法适合于任何领域或任务。

2.8.3 丑小鸭定理

丑小鸭定理（Ugly Duckling Theorem）是 1969年由渡边慧提出的 [Watan-able, 1969]。“丑小鸭与白天鹅之间的区别和两只白天鹅之间的区别一样大”。这个定理初看好像不符合常识，但是仔细思考后是非常有道理的。因为世界上不存在相似性的客观标准，一切相似性的标准都是主观的。如果以体型大小的角度来看，丑小鸭和白天鹅的区别大于两只白天鹅的区别；但是如果以基因的角度来看，丑小鸭与它父母的差别要小于他父母和其他白天鹅之间的差别。

2.8.4 奥卡姆剃刀

习题 2-1 分析为什么平方损失函数不适用于分类问题。

对于分类问题，我们的分类结果一般是0/1表示，如果仅仅使用MSLoss来计算预测结果和实际结果显得十分简单粗暴，我们更好的方式是·是衡量这二者的概率分布的差异，就是交叉熵，因为它的设计初衷，就是要衡量两个概率分布之间的差异。

习题 2-2 在线性回归中，如果我们给每个样本 $\left(\mathbf{x}^{(n)}, y^{(n)}\right)$ 赋予一个权重 $r^{(n)}$ ，经验风险函数为 $\mathcal{R}(\mathbf{w})=\frac{1}{2} \sum_{n=1}^{N} r^{(n)}\left(y^{(n)}-\mathbf{w}^{\mathrm{T}} \mathbf{x}^{(n)}\right)^{2}$ 4 计算其最优参数 w∗，并分析权重 r(n) 的作用。

今天的文章FDU邱锡鹏《神经网络与深度学习》第 2 章机器学习概述及习题全解分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/66028.html

FDU邱锡鹏《神经网络与深度学习》第 2 章 机器学习概述及习题全解