此前学习和实现卡尔曼滤波花费了很多时间,其实想要理解其原理并不算很复杂。只是简单套用卡尔曼滤波的公式,而没有系统理解公式里面每个变量的缘来,不去理解卡尔曼滤波器的迭代过程和原理,在实现和调试系统的时候无疑是会找不着北的。本文将指引你轻松理解卡尔曼滤波。
1. 一个简单的场景
假设我们开发了一台无人机(假设它的名字是Eva),想要用它来在城市中送快递,Eva身上有一些传感器,可以让我们知道它的速度v(比如三维空间中沿x,y,z各轴的速度大小),同时Eva身上还有GPS系统、气压计等设备,可以获知它的位置p(比如经纬度,海拔等),也就是说我们可以实时**观测**Eva的状态。
那么我们可以把Eva的某一个时刻的状态表示为一个向量:
2. 不确定性和相关性
虽然我们比较肯定Eva此时的状态,但是无论如何系统总是会存在误差的,无论是计算上,还是传感器的检测上,所以我们只能认为当前状态是当前真实状态的一个最优估计。那么我们不妨认为Eva的当前状态服从一个高斯分布,如下图所示:
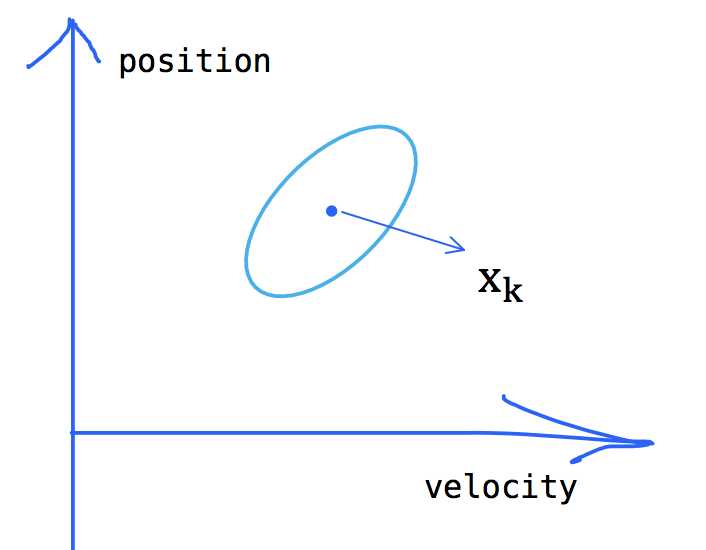
高斯分布的中心 μ μ 就是图中的 x̂ k x ^ k :
对于方差
σ2 σ 2
(也就是图中的椭圆的范围),因为我们有两个变量,所以可以用一个协方差矩阵
Pk P k
来表示(如果对协方差矩阵还不了解,
戳此了解):
所以Eva的真实状态可能就位于上图椭圆的范围内,位于圆心的概率最大。
3. 预测下一个位置的系统状态和系统误差
Ok,接下来我们需要通过Eva当前的状态,运用一些物理学的知识来预测它的下一个状态,通过简单的物理学知识,通过k-1时刻的位置和速度,可以推测下一个时刻的状态为:
写成矩阵形式就是:
此处的
Fk F k
就是
状态转移矩阵。
Eva的系统误差通过协方差矩阵
Pk P k
来表示,根据协方差矩阵的性质:
那么我们所预测的Eva下一个时刻的状态误差为:
4. 考虑系统内部控制
为了能让Eva到达任何地方,毫无疑问我们需要对它进行控制,比如加速和减速,假设某个时刻我们施加给Eva的加速度是 a a ,那么下一时刻的位置和速度则应该为:
今天的文章轻松理解卡尔曼滤波分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/66030.html
