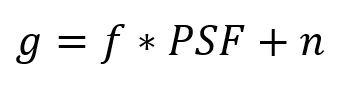自适应滤波基本原理及应用_自适应滤波基本原理及应用

        本文简单实现了光学与光电技术论文《基于改进自适应Wiener滤波的光学合成孔径系统图像复原算法》(2015年2月第13卷第一期)提及的改进自适应维纳滤波算法。

        光学系统成像（降质模型）如下：

        f表示目标物，PSF表示点扩散函数，*代表卷积，g为得到的像。

        作者在原文中表明，如果局部图像方差小而局部噪声方差大， 说明图像总体变化不大，比较平滑，而噪声波动范围较大。为使图像平滑增强，更大程度地抑制噪声，维纳滤波中K的值需要取得更大；相反，如果局部图像方差大而局部噪声方差小，K的值取得更小，来保留图像的纹理细节。因此，作者使用退化图像的局部噪声方差与局部图像方差之比来定义K。

        原文算法描述如下：

        当然，第三步是把K带入维纳滤波中进行复原。

        算法中ones(3)，表示一个3*3矩阵，且所有元素为1；ones(3)/50表示所有元素为0.02.（但是如果除以50得到的均匀算子使得z1图像过暗，最后K值过大，影响复原效果，在这里改为除以9，相当于一个3*3的均值滤波）由于算法比较容易理解，所以不在这过多的赘述。实验仍直接导入Psf数据对图像进行卷积，并加入均值为0，方差为0.01的高斯噪声(normrnd)。

f=rgb2gray(imread('timg.jpg'));
[m,n]=size(f);
psf=load('psf_304.txt');
Psf=psf./sum(sum(psf));
C = imfilter(f,Psf,'conv'); 
g=C+uint8(normrnd(0,0.01,m,n));%模拟成像

z=ones(3)/9;
z1=imfilter(g,z,'conv');
delta_z1=sum(sum((double(f)-double(z1)).^2));
delta_g=sum(sum((double(f)-double(g)).^2));   
delta_n=abs(delta_g-delta_z1);
K=delta_n/delta_g;
fn=deconvwnr(g,Psf,K);%最后复原图像

与之前的迭代找最优解K（改进自适应维纳滤波的实现——基于改进自适应Wiener滤波的光学合成孔径系统图像复原算法 宋程 耿安兵）相比：

 左：本实验效果，（K=0.0201，耗时0.051850s，psnr=22.4726）右：迭代找最优解效果。(K=0.0058，耗时30.841028秒，psnr=22.9002) 。模糊图像g的psnr：20.0285

虽然复原效果不如迭代的效果，但节省了大量的计算的时间。（当然迭代设置的比较慢）

今天的文章自适应滤波基本原理及应用_自适应滤波基本原理及应用分享到此就结束了，感谢您的阅读。