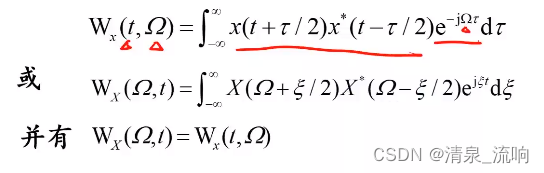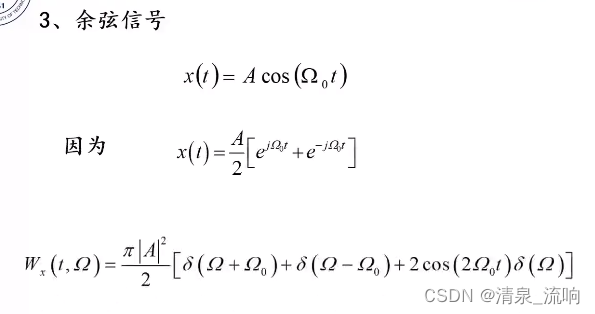一、Winger-Ville分布(WVD)定义
信号x(t)的自Wigner分布定义为其瞬时相关函数关于滞后
Winger于1932年提出并用量子力学。1948年Ville应用于信号分析,并讨论数学基础、时频分布的统一表示形式、WVD定义和性质等,论文、成果称“所有时频分布之母”。

两个时域信号卷积后的WVD等于各自WVD在时间轴上的卷积
两个信号相乘后的WVD等于各自WVD在频率轴上的卷积。当我们对无限长时域信号加窗截断时,只影响其频域分辨率,不影响其时域分辨率。
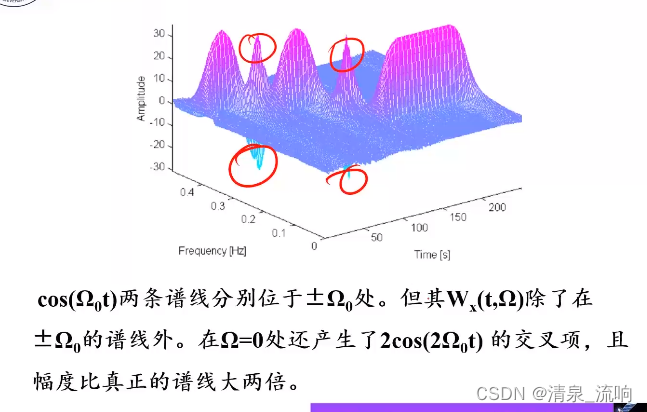
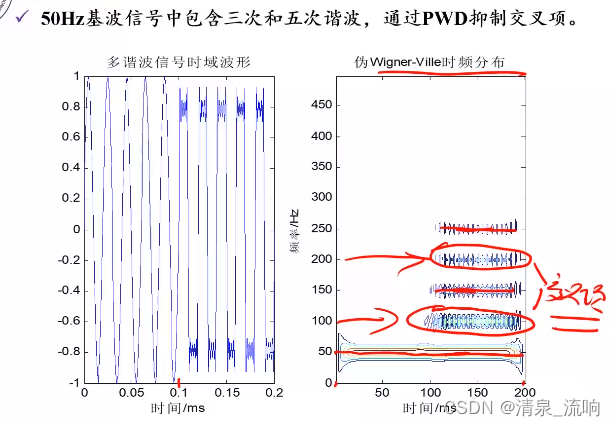
两个信号相加后的WVD,并不等于各自WVD的相加,还要加上两个信号的互WVD。这些互WVD是对相加后信号WVD的干扰,在时频分布中,称它们为交叉项干扰。
WVD的缺点
1、WVD有交叉项的存在,使得两个信号和的分布已不再是两个信号各自分布的和。
2、由于WVD是信号能量随时间一频率的分布,因此从理论上讲,


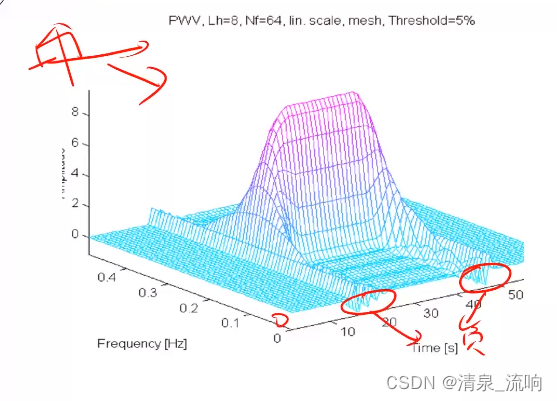
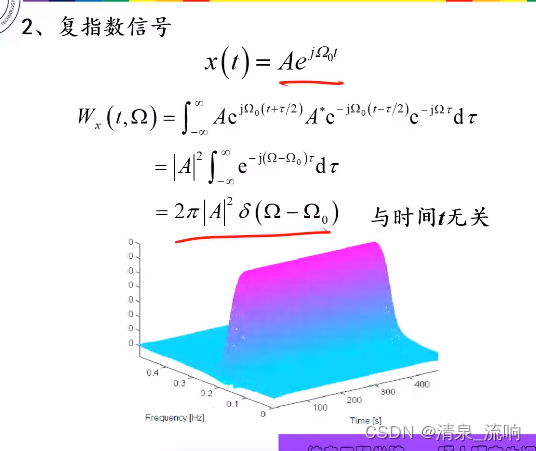
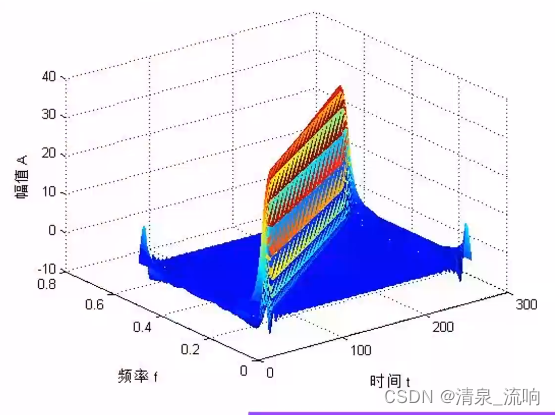
三、常用信号的WVD
四、离散WVD的实现
与DFT一样,计算机上具体实现WVD必须进行:(1)对x(t)进行加窗截取(2)对t和Ω离散化

1、将时频表示



2、时频分布的信号二次型其线性特性受到破坏,即两个信号之和的时频分布不是各自时频分布之和,也就是产生了交叉项(相干项)。WVD的二次型形成(信号的相干形成)相对来说具有较好的时频分辨率(或称时频集聚),而且交叉项也相对较小。
五、时频分布的性能评价
时频信号分析的大多数应用与非平稳信号的多分量抽取有关。通常希望时频信号分析具有以下功能。
1、能够确定信号中存在的信号分量个数;
2、能够识别信号分量与交叉项;
3、能够分辨出在时频平面上相距很近的信号分量;
4、能够估计信号各个分量的瞬时频率。
时频分析方法的性能评价:时频聚集性和交叉项
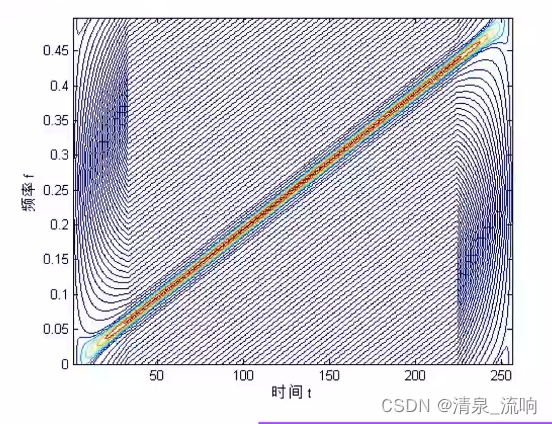
线性调频信号的时频分布如下:
参考视频:
https://www.bilibili.com/video/BV1wS4y1D7ng/?p=11&spm_id_from=pageDriver&vd_source=77c874a500ef21df351103560dada737
今天的文章现代信号处理——时频分析与时频分布(Wigner-Ville分布)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/66895.html