1. 编程号首页

趣玩算法–OpenCV华容道AI自动解题

编程小号 • • 未分类

趣玩算法–OpenCV华容道AI自动解题学更好的别人，做更好的自己

学更好的别人，做更好的自己。——《微卡智享》

前言

上一期《整活！我是如何用OpenCV做了数字华容道游戏！（附源码）》实现数字华容道游戏的制作，相对来说也比较简单，所以本篇是在这个基础上我们提升一下难度，用代码来实现数字华容道的AI自动还原。

 

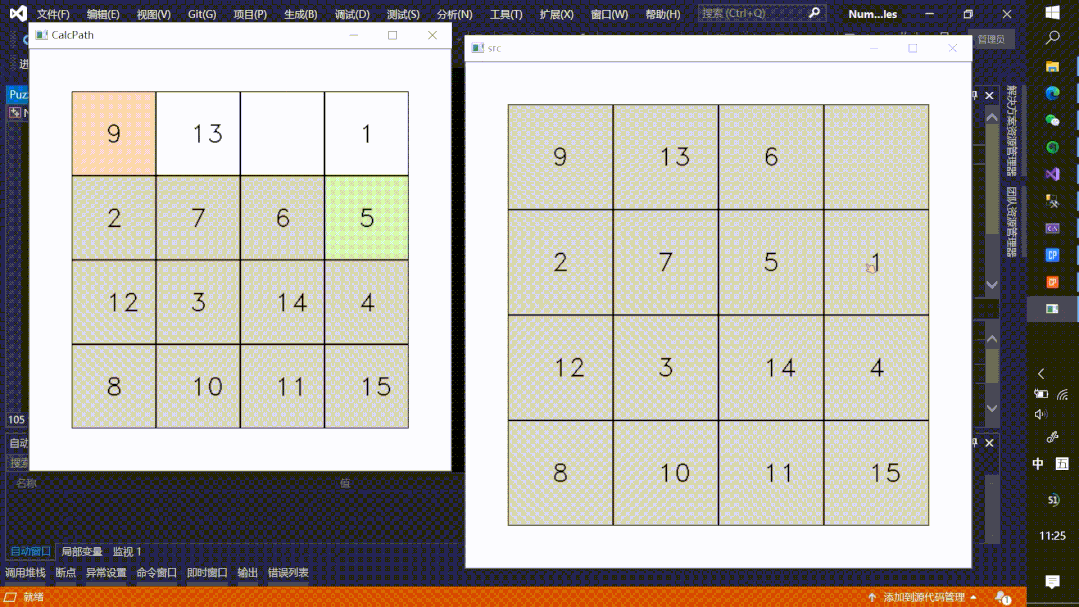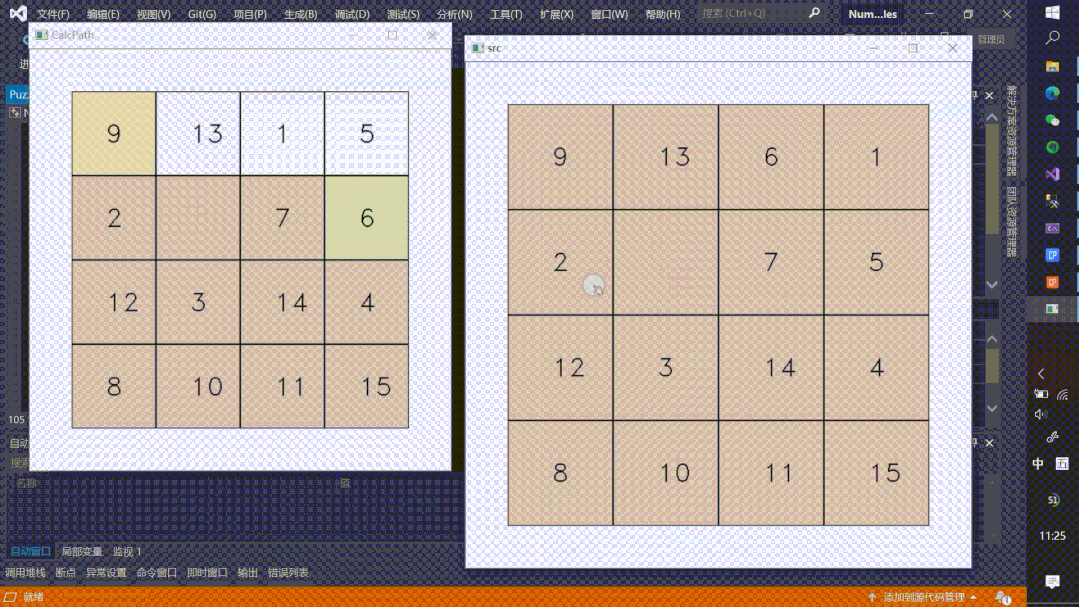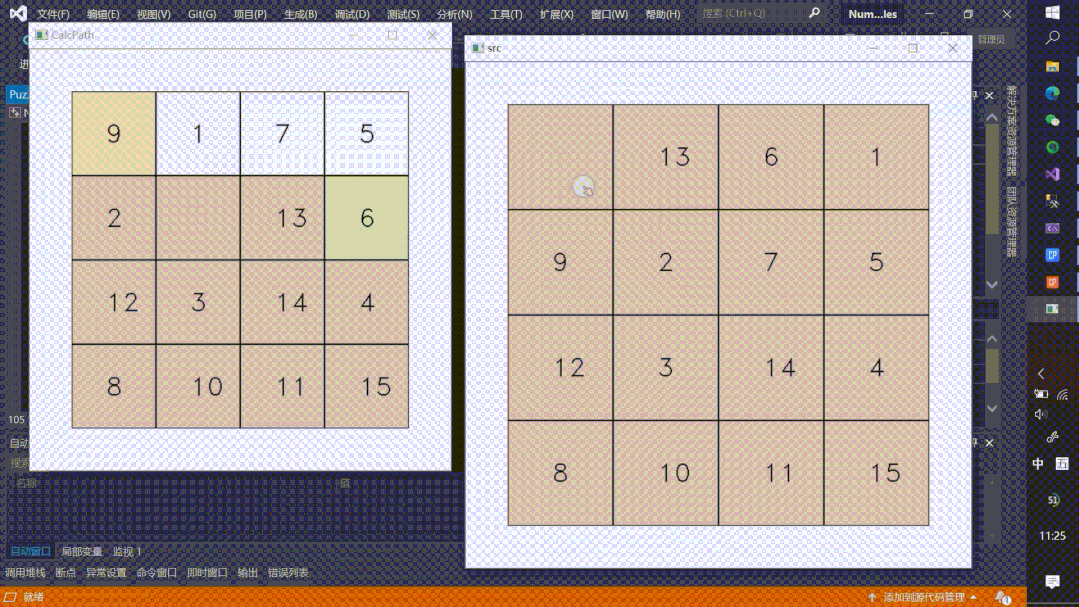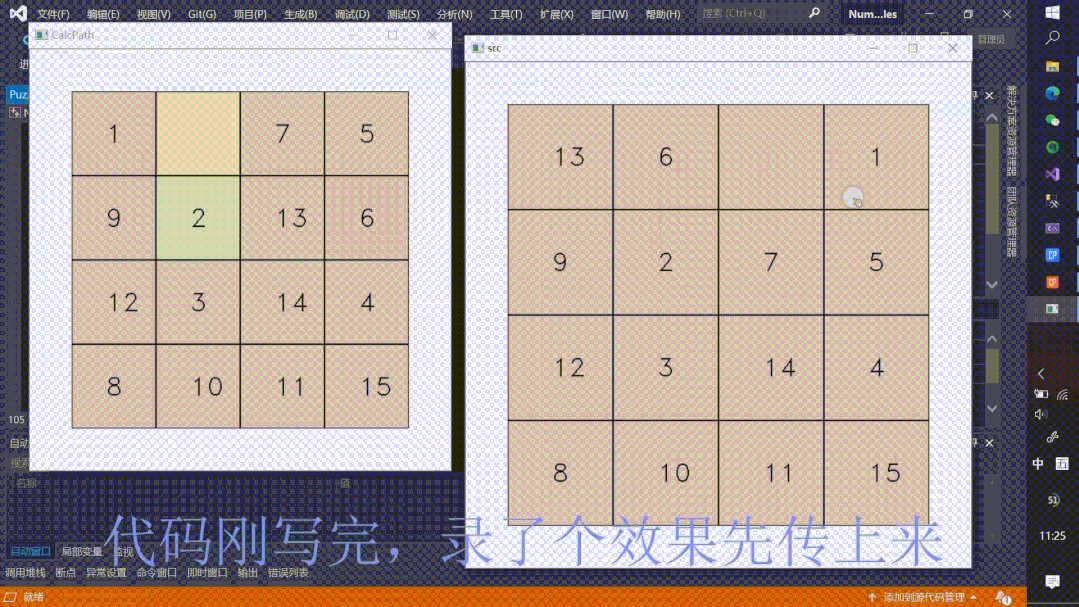
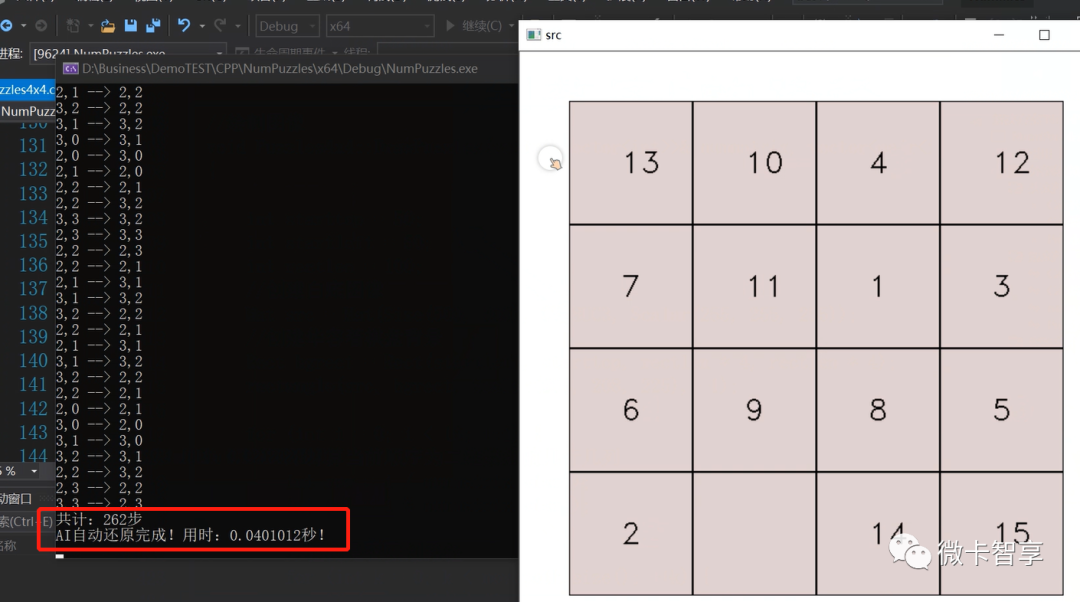
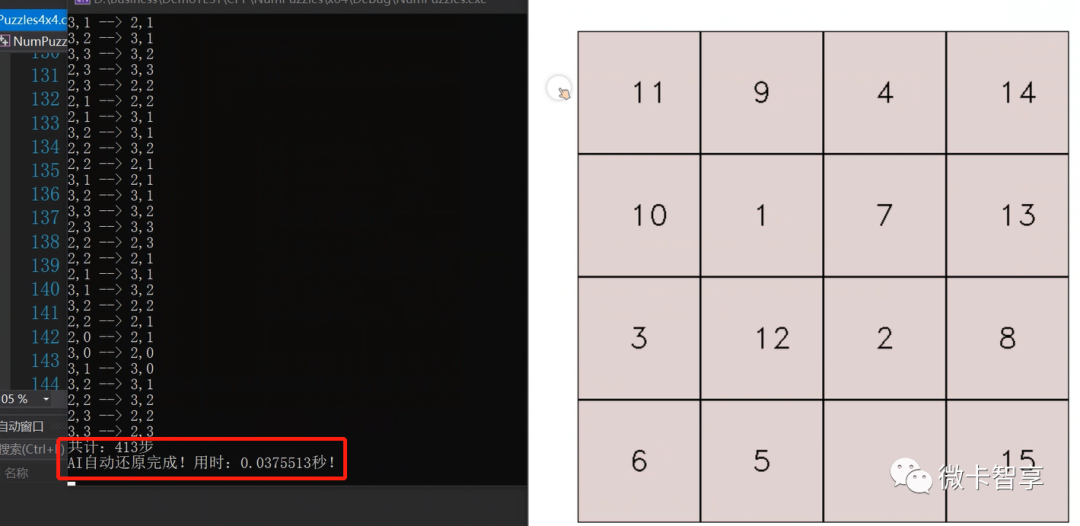
实现效果

de26933ec410f57ea70edce64bf9f10e.gif

完整的视频思路讲解可以点下面的视频进行观看。‍

趣玩算法–数字华容道AI自动解题

 

Q1

华容道自动还原的核心点？

想要用程序实现数字华容道的自动还原，需要掌握什么？

 

1.数字华容道的解题方法，这个网上教学有不少。

2.怎么用程序实现数字移动到指定位置。（核心就是路径规划算法）。

路径规划算法

cb7e67e23665b26e9ff230f9cedbded2.png

微卡智享

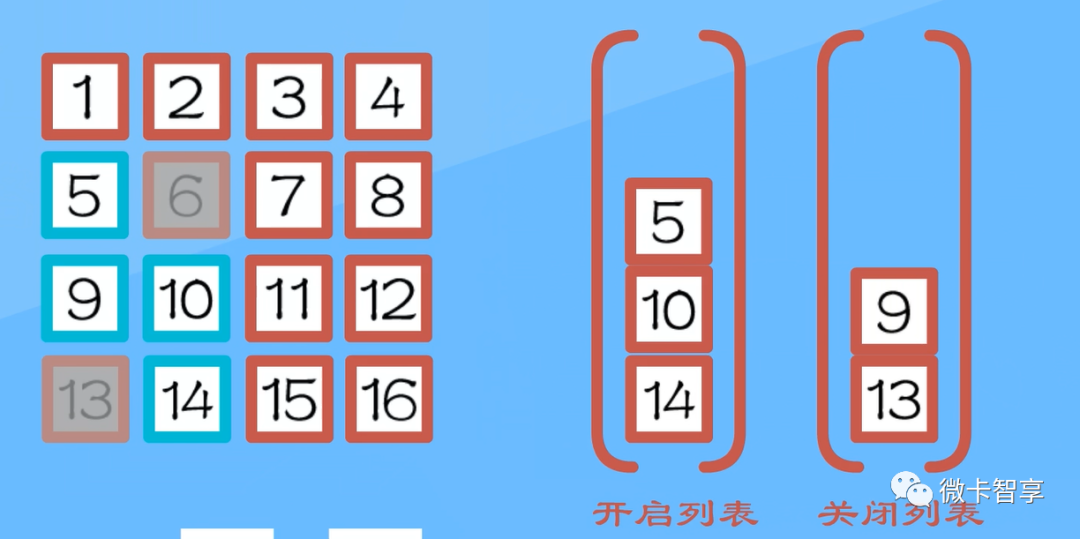
数字华容道的路径规划算法是也是基于A星算法原理实现的，区别就是A星算法是允许斜线移动，在计算当前要规划的点时，需要计算周围8个邻近点，而数字华容道行动时不允许走斜线，所以只能计算上下左右四个直线方向的点。

864f48039b88a755d8e463a13bc1a9f1.png

图中计算当前要行动的点是数字10，数字华容道计算时只计算6、9、11、14，而A星算法除了上面4个还要计算5、7、13、15。

01

直线移动距离相等问题

也正是因为数字华容道只允许走直线，所以要计算的点离终点距离有可能会存在2个路径是相等的，怎么解决这个问题呢？

fef6842702072f7c4a19cc7b63e9f826.png

上图中13到6的移动，红色线路和绿色线路用的体力是一样的都是3

解决上图这个问题，算法里加入了优先移动方向的参数，如上图取出13邻居可移动的数字为9和14，默认13到9和14的用的体力都是1，如果设置优先移动方向为上，那就变为13到9的体力为0.9，而13到14的体力还是1，这样整个计算下来红色线路要比绿色线路节省体力，最终规划的线路就是红色线路。

0cfe454b1188d52ddb1e987ae3d97e86.png

优先移动方向枚举

eec3f5af2ab46f26cdfcad75b46cbabc.png

37c01984d54f1874dadb2801d28f832d.png

计算消耗的体力，加入优先行动方向的区分

02

数据结构

路径规划中每取到一个到终点用的体力最少的点时，就用这个点继续开始往下查找，所以数据结构上用链表的方式，每个点都有其父节点，直接找到终点后通过终点的父节点一步步的反推到起点，即是我们的行动路径。

1ea66d79e30a92f870c9acd5a571413e.png

定义的数据结构 

20b51b13ae6fc0b9402c5d40c42365d8.png

加入地图障碍、开户列表、关闭列表

定义了一个开启列表和一个关闭列表，其中开启列表中存放着还未计算的所有点，关闭列表中存放着已经计算过的点。每次从开启列表中取出到终点体力最少的点，都存放到关闭列表中，还有找出这个点的上下左右可移动的点，当这几个点中超过地图范围或是在障碍点中，以及已经在关闭列表中时，就不做为可移动的点了，这样可以减少循环的计算量。

32c58ad2e820fba4fbe276103ff05588.png推荐看视频中动画的讲解

核心代码

CalcPathPlan.h

#pragma once
#include <iostream>
#include <vector>
#include <list>


using namespace std;


//修改后简化版的A*路径规划,不存在斜线移动，计算的邻近点也只为上下左右4个
struct CalcPos
{
public:
  int col; //X坐标位置  
  int row; //Y坐标位置
  float F, G, H; //F=G+H   G为起点到当前点已经移动的距离，H为当前点到终点的距离 
  CalcPos* parent; //父节点


  CalcPos(int _row, int _col) : row(_row), col(_col), F(0), G(0), H(0), parent(NULL)
  {
  }
};


//优先移动方向
enum DirectFirst {
  Up = 0,
  Down = 1,
  Left = 2,
  Right = 3,
  None = 9
};


class CalcPathPlan
{
private:
  CalcPos* findPath(CalcPos& startPos, CalcPos& endPos);
  //计算临近的上下左右4个点
  vector<CalcPos*> getSurroundPos(const CalcPos* pos);
  //判断当前的点是否可以列入计算列表
  bool isCanCalc(const CalcPos* pos, const CalcPos* target);
  //判断点是否在开启或是关闭列表中
  CalcPos* isInList(const list<CalcPos*>& list, const CalcPos* pos);
  //检测障碍点
  bool isInSites(const int row, const int col) const;
  //从开启列表中返回F值最小的节点 
  CalcPos* getLeastFpoint();


  //计算FGH值 
  float calcG(CalcPos* temp_start, CalcPos* pos);
  float calcH(CalcPos* pos, CalcPos* end);
  float calcF(CalcPos* pos);


  vector<vector<int>> sites;  //华容道棋盘 0-可通行，1-障碍点
  list<CalcPos*> openList;  //开启列表 
  list<CalcPos*> closeList; //关闭列表 


public:
  //参数优先移动方向
  int DirectFirst = DirectFirst::Up;
  //初始化地图
  void InitSites(vector<vector<int>> _sites);
  //获取到路径
  vector<pair<int,int>> GetPath(pair<int, int>& startPos, pair<int, int>& endPos);
};

CalcPathPlan.cpp

#include "CalcPathPlan.h"


CalcPos* CalcPathPlan::findPath(CalcPos& startPos, CalcPos& endPos)
{
  //首先写入起点,拷贝开启一个节点，内外隔离
  CalcPos* firstpt = new CalcPos(startPos.row, startPos.col);
  firstpt->H = calcH(firstpt, &endPos);
  firstpt->F = calcF(firstpt);


  openList.push_front(firstpt);


  while (!openList.empty()) {
    //找到F值最小的点
    auto curPoint = getLeastFpoint();


    //从开启列表中删除
    openList.remove(curPoint);
    //存放到关闭列表中
    closeList.push_front(curPoint);




    //1.找到当前点周围四个点中可以通过的点
     auto surroundPos = getSurroundPos(curPoint);


    for (auto& target : surroundPos) {
      //2.对某一个点，如果不在开启列表中，加入到开启列表中，设置当前格为父节点，计算F,G,H的值
      CalcPos* targetpos = isInList(openList, target);
      if (!targetpos) {
        //计算F,G,H的值
        target->G = calcG(curPoint, target);
        target->H = calcH(target, &endPos);
        target->F = calcF(target);


        target->parent = curPoint;


        //插入到开启列表中
        openList.push_front(target);
      }
      //3.对某个点在开启列表中计算G值，如果比原来的大，就什么都不做
      //否则设置它的父节点为当前点，并更新G和F
      else {
        int tempG = calcG(curPoint, targetpos);
        if (tempG < targetpos->G) {
          targetpos->parent = curPoint;


          targetpos->G = tempG;
          targetpos->F = calcF(targetpos);
        }
      }


      CalcPos* resPoint = isInList(openList, &endPos);
      //返回列表里的节点指针，不要用原来传入的endpoint指针，因为发生了深拷贝 
      if (resPoint)
        return resPoint;
    }
  }
  return NULL;
}


//计算当前点的可移动的上下左右点
vector<CalcPos*> CalcPathPlan::getSurroundPos(const CalcPos* pos)
{
  vector<CalcPos*> surroundPos;


  //上方点
  if (isCanCalc(pos, new CalcPos(pos->row - 1, pos->col))) {
    surroundPos.push_back(new CalcPos(pos->row - 1, pos->col));
  }
  //下方点
  if (isCanCalc(pos, new CalcPos(pos->row + 1, pos->col))) {
    surroundPos.push_back(new CalcPos(pos->row + 1, pos->col));
  }
  //左方点
  if (isCanCalc(pos, new CalcPos(pos->row, pos->col - 1))) {
    surroundPos.push_back(new CalcPos(pos->row, pos->col - 1));
  }
  //右方点
  if (isCanCalc(pos, new CalcPos(pos->row, pos->col + 1))) {
    surroundPos.push_back(new CalcPos(pos->row, pos->col + 1));
  }


  return surroundPos;
}


bool CalcPathPlan::isCanCalc(const CalcPos* pos, const CalcPos* target)
{
  //坐标小于0直接不计算了
  if (target->col < 0 || target->row < 0
    //计算的点与当前一致也不计算
    || (target->col == pos->col && target->row == pos->row)
    //判断点在障碍点中不计算
    || isInSites(target->row, target->col)
    //如果点在关闭列表中也不计算
    || isInList(closeList, target))
    return false;
  else {
    return true;
  }
}


//判断开启/关闭列表中是否包含某点
CalcPos* CalcPathPlan::isInList(const list<CalcPos*>& list, const CalcPos* pos)
{
  //判断某个节点是否在列表中，这里不能比较指针，因为每次加入列表是新开辟的节点，只能比较坐标
  for (auto p : list)
    if (p->col == pos->col && p->row == pos->row)
      return p;
  return NULL;
}


bool CalcPathPlan::isInSites(const int row, const int col) const
{
  if (col < 0 || row < 0 || row >= sites.size()
    || col >= sites[0].size()) return true;
  return sites[row][col] == 1;
}


//获取开启列表中F值最小的点才行动计算点
CalcPos* CalcPathPlan::getLeastFpoint()
{
  if (!openList.empty())
  {
    auto resPos = openList.front();
    for (auto& pos : openList)
      if (pos->F < resPos->F)
        resPos = pos;
    return resPos;
  }
  return NULL;
}


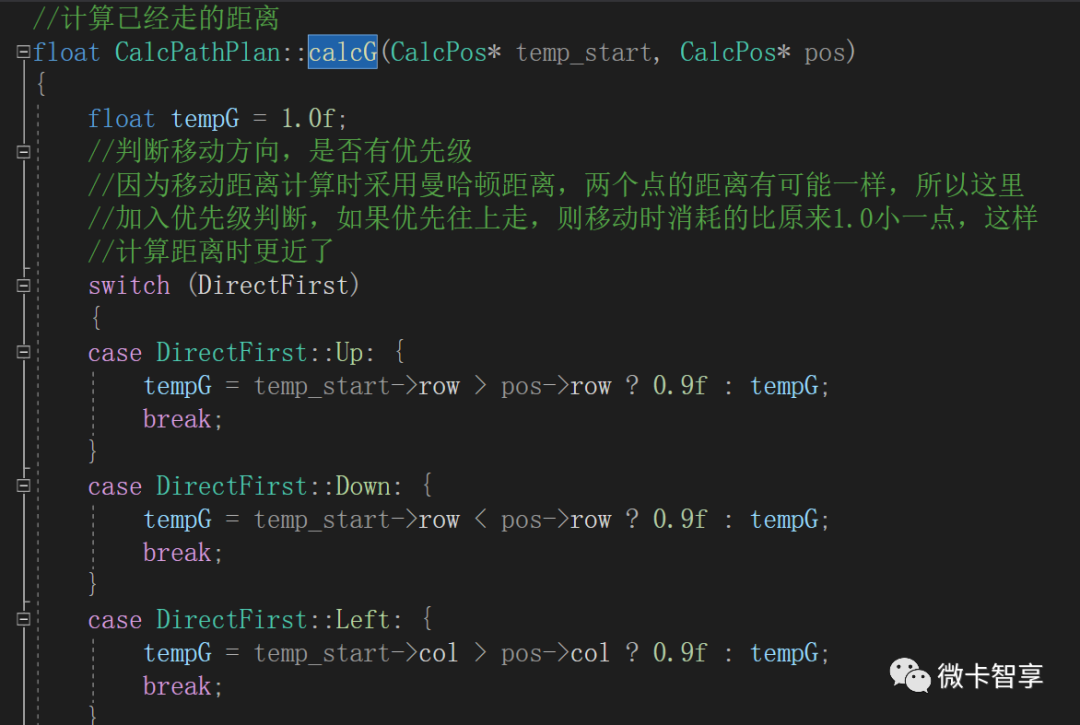
//计算已经走的距离 
float CalcPathPlan::calcG(CalcPos* temp_start, CalcPos* pos)
{
  float tempG = 1.0f;
  //判断移动方向，是否有优先级
  //因为移动距离计算时采用曼哈顿距离，两个点的距离有可能一样，所以这里
  //加入优先级判断，如果优先往上走，则移动时消耗的比原来1.0小一点，这样
  //计算距离时更近了
  switch (DirectFirst)
  {
  case DirectFirst::Up: {
    tempG = temp_start->row > pos->row ? 0.9f : tempG;
    break;
  }
  case DirectFirst::Down: {
    tempG = temp_start->row < pos->row ? 0.9f : tempG;
    break;
  }
  case DirectFirst::Left: {
    tempG = temp_start->col > pos->col ? 0.9f : tempG;
    break;
  }
  case DirectFirst::Right: {
    tempG = temp_start->col < pos->col ? 0.9f : tempG;
    break;
  }
  default:
    tempG = 1.0f;
    break;
  }


  //判断是不是初始的节点，如果是初始节约，则其父节点为空
  int parentG = pos->parent == NULL ? 0 : pos->parent->G;
  //两个G相加用于判断是走直线和斜线所消耗的总G
  return parentG + tempG;
}


float CalcPathPlan::calcH(CalcPos* pos, CalcPos* end)
{
  //计算终点到当前点的距离，因为不用斜着走，所以采用曼哈顿距离计算
  return abs(end->col - pos->col) + abs(end->row - pos->row);
}


float CalcPathPlan::calcF(CalcPos* pos)
{
  //公式 F=G+H
  return pos->F = pos->G + pos->H;
}




//初始化地图
void CalcPathPlan::InitSites(vector<vector<int>> _sites)
{
  sites = _sites;
}


vector<pair<int, int>> CalcPathPlan::GetPath(pair<int, int>& startPos, pair<int, int>& endPos)
{
  CalcPos sPos = CalcPos(startPos.first, startPos.second);
  CalcPos ePos = CalcPos(endPos.first, endPos.second);
  CalcPos* result = findPath(sPos, ePos);
  vector<pair<int, int>> path;
  //返回路径，如果没有找到路径，返回空链表
  while (result) {
    pair<int, int> curpath(result->row, result->col);
    path.insert(path.begin(), curpath);
    result = result->parent;
  }
  return path;
}

华容道代码编写

78e2ab7c90515c712faf617a2a27dd07.png

微卡智享

01

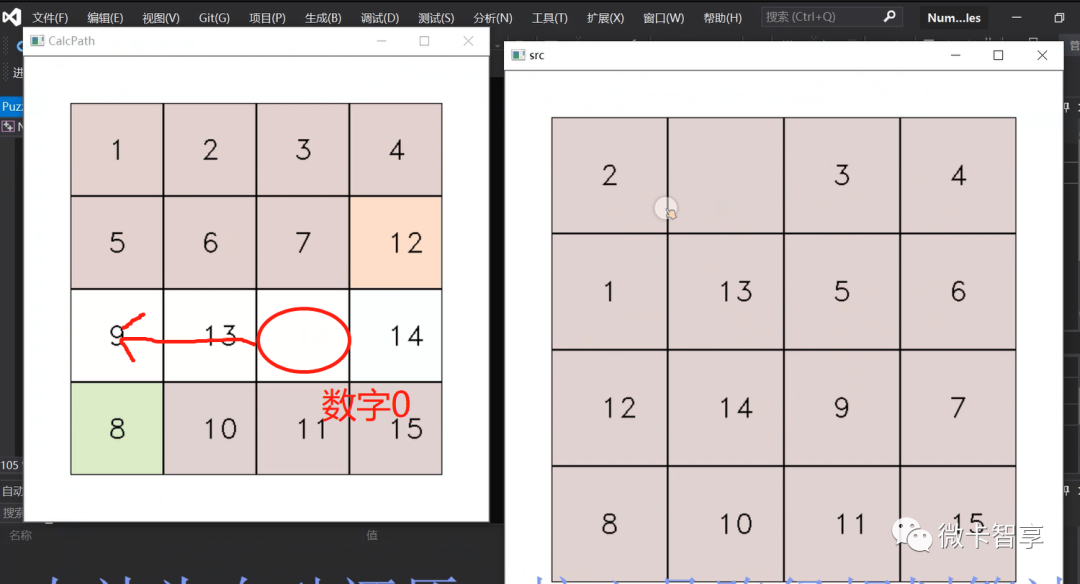
根据规划路径怎么移动

dfeac1b972f91b87122aa4d190d77dde.png

从上图中可以看到，通过路径规划已经计算出还原数字8的行动路径了，需要实现8在这个行动路径上移动，最终就是要把数字0（也就是空白格）移动到8的下一步行动格上（即现在9的位置），移动时就是根据当前格与到移动的格进行数字互换即可。

d105b37e2030e66e8d1702cfaa0cee72.png

当移动完后0和数字8再进行位置交换，继续刚才的步骤，0再移动到数字9的位置，这时8再设置成为障碍点，这样规划0到9的位置时不会经过数字8（上一步也这样处理），等移动到位置后再把障碍点取消进行互换。

数字0移动的核心代码

int Puzzles4x4::ZeroMove(vector<vector<int>>& vts, vector<vector<int>>& sites, pair<int, int>& endPos, int MoveDirect)
{
  pair<int, int> ZeroPos = GetPos(vts, 0);
  vector<pair<int, int>> zeropath;


  if (ZeroPos.first == endPos.first && ZeroPos.second == endPos.second) {
    return 0;
  }
  zeropath = FindPath(sites, ZeroPos, endPos, MoveDirect);
  //3.3.1 开始移动0到当前位置,从第一步开始，因为起点不动
  for (int k = 1; k < zeropath.size(); ++k) {
    //cout << "zeropath:" << zeropath[k].first << " " << zeropath[k].second << endl;
    //当前位置与前一位置与换
    SwapPos(vts, zeropath[k], zeropath[k - 1]);
  }


  return zeropath.size();
}


//两个点交换位置
void Puzzles4x4::SwapPos(vector<vector<int>>& vts, pair<int, int>& firstPos, pair<int, int>& secondPos)
{
  //插入还原步骤
  pair<pair<int, int>, pair<int, int>> curstep(firstPos, secondPos);
  VetRestoreSteps.push_back(curstep);


  int tmpnum = vts[firstPos.first][firstPos.second];
  vts[firstPos.first][firstPos.second] = vts[secondPos.first][secondPos.second];
  vts[secondPos.first][secondPos.second] = tmpnum;
}

02

华容道中特殊步骤处理

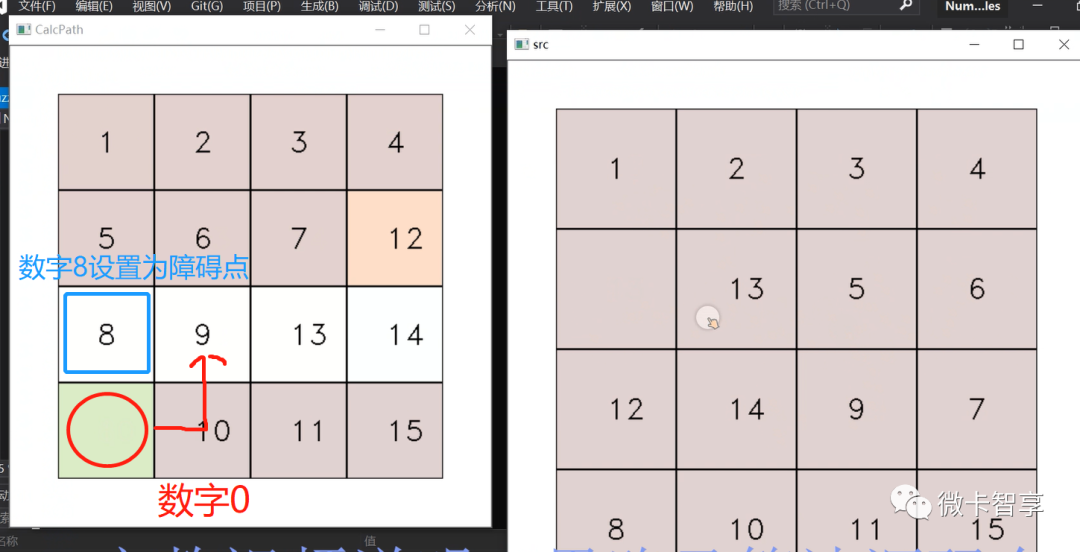
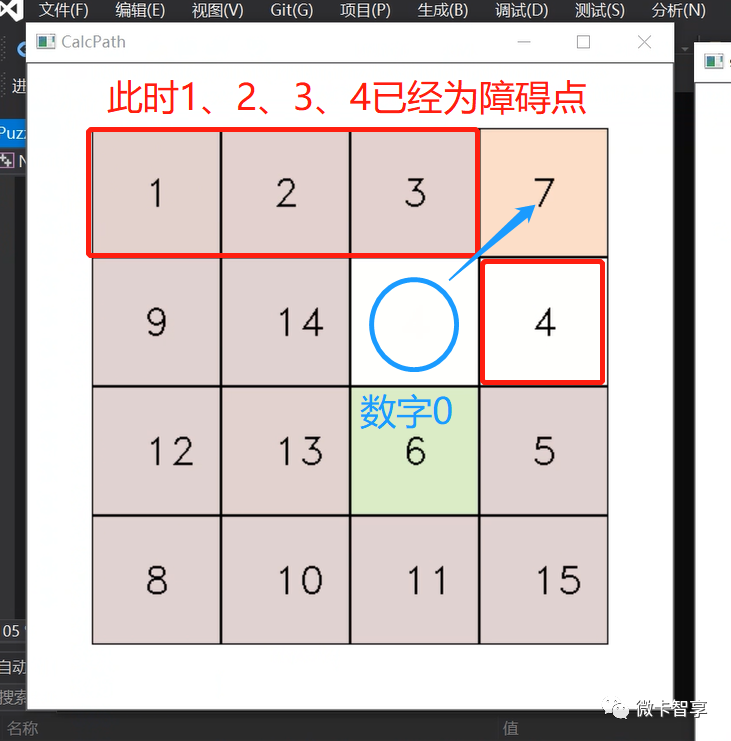
第一、二行最右侧处理

965fcdb1bb7820247ba7428da6c1c727.png

数字0无法移动到数字7的位置

上图中可以看出，数字4按路径规划移动到第二行第四格时，按我们定义的规则，现在数字4已经设置为障碍点了，同时因为数字1、2、3已经归位，所以也设置为障碍点，此时数字0移动到数字7是无路可走的，这里就需要进入到特殊步骤的环节了。

637b8bcab4ab51cb31760ae842011938.png

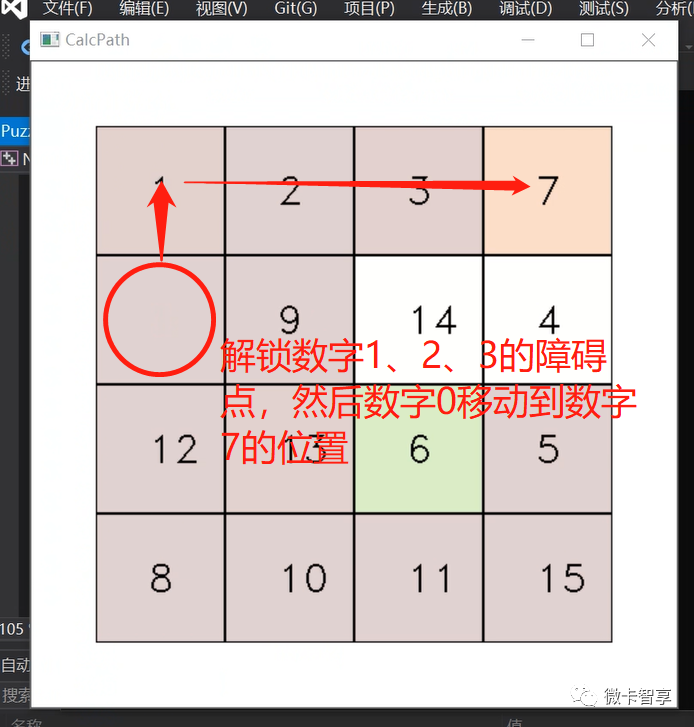
首先将数字0移动到数字9的位置

f8ddc5e3fb3f7f0c4147e5aad2dd9a11.png

然后数字0移动到数字7的位置

按上面的方法，首先把数字1、2、3解锁障碍点，然后将数字0移动到数字7的位置，这里就可以体现到路径规划中加入方向参数的作用了，优先按向上行走，走的路线肯定是上图中的方案。

a40cf446d3999910f063e3939252a2a0.png

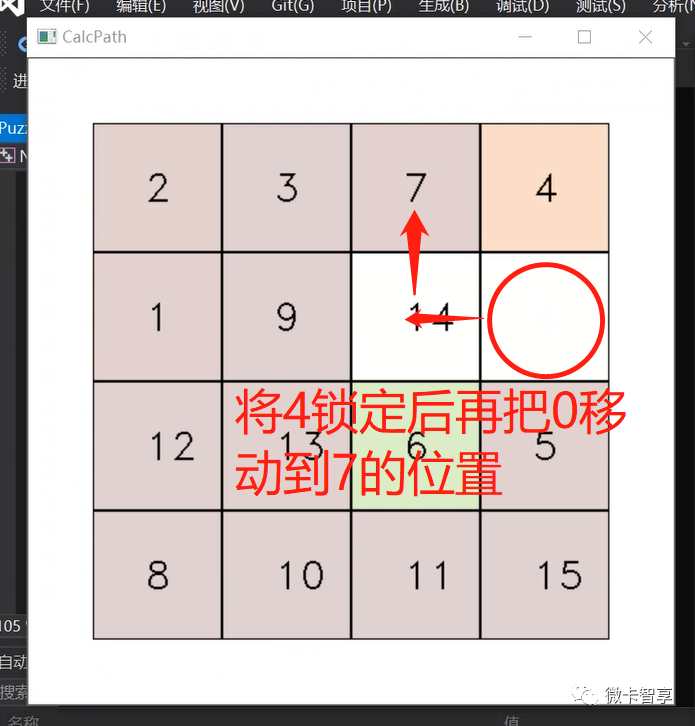
0到达位置后和4进行互换

3b5dfd2944c0eb19628a133165a3e03c.png

重新移动0的位置到7

613552e5d542a348922b10f7ac136905.png

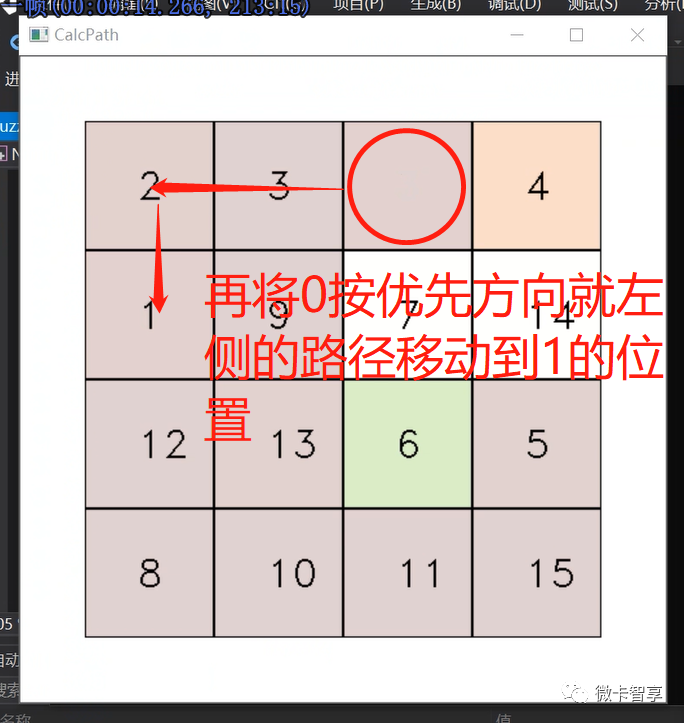
将0按优先左移的路径规划移动到1的位置，这样数字1、2、3就可以正常还原回去了

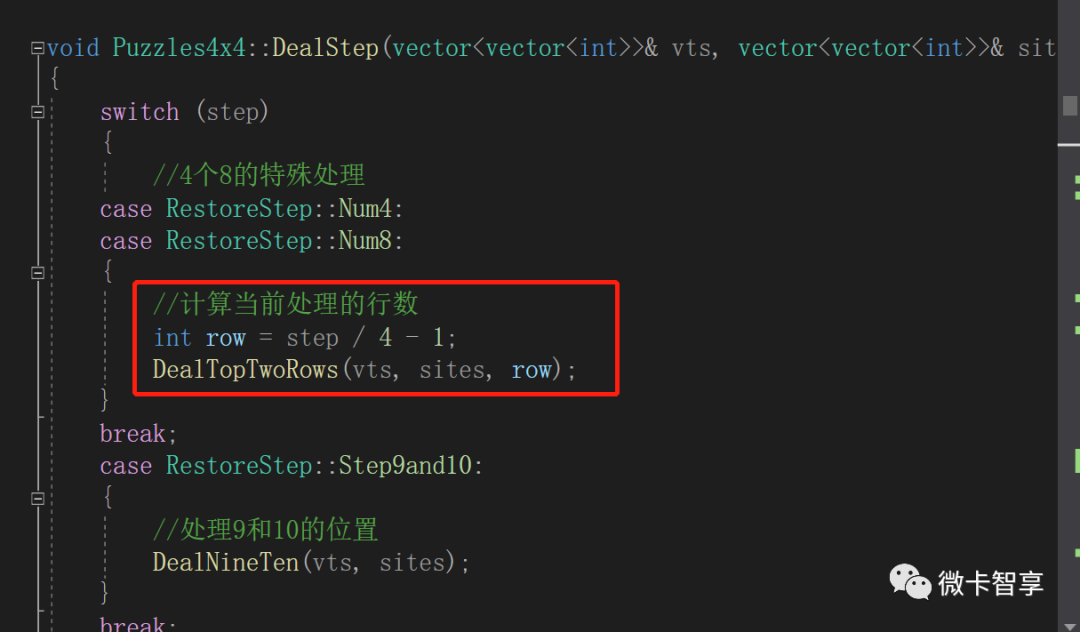
按上面的流程就处理好数字4了，数字8的原理和4是一样的，所以代码中我们写了一个方法，只是在开始判断当前处理的是第几行即可。

核心函数

void Puzzles4x4::DealTopTwoRows(vector<vector<int>>& vts, vector<vector<int>>& sites, int row)
{
  //1.先将0移动到当前要处理的行的下面格
  pair<int, int> endPos(row + 1, 0);
  ZeroMove(vts, sites, endPos, DirectFirst::Left);


  //2.解锁处理行前面的障碍点，用0的位置优先移动到计算点
  for (int i = 0; i < sites[row].size(); ++i) {
    sites[row][i] = 0;
  }
  endPos.first = row;
  endPos.second = 2;
  ZeroMove(vts, sites, endPos, DirectFirst::Up);


  //3.数字0再和当前要处理的点进行位置互换，将我们4或8位置移动到对应后锁定
  endPos.first = row + 1;
  endPos.second = 3;
  //防止移动点是锁定的，将改为可移动
  sites[endPos.first][endPos.second] = 0;
  ZeroMove(vts, sites, endPos, DirectFirst::Right);
  //设置为锁定障碍点
  sites[row][3] = 1;


  //4.将数字0移动到第二步位置后还原当前行前三个数字
  endPos.first = row;
  endPos.second = 2;
  ZeroMove(vts, sites, endPos);


  //5.将0优先按左移的方式把原来行前面的数字还原回来
  endPos.first = row + 1;
  endPos.second = 0;
  ZeroMove(vts, sites, endPos, DirectFirst::Left);
}

6a6dbe13335611b82a5d94b13114882a.png

调用时的处理

第三和、四行处理

8aed711bbb8e62b9977ef0a8707115d0.png

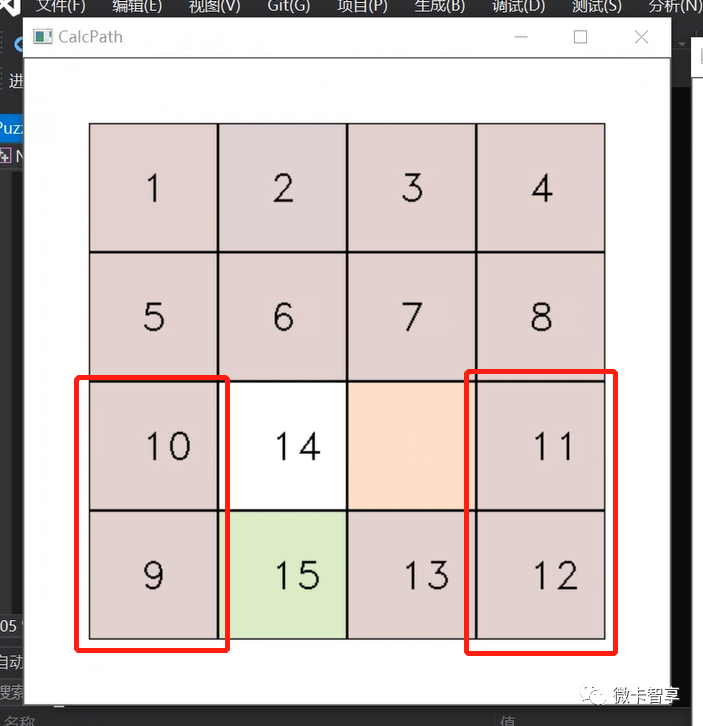
三、四行把9和10、11和12移动到两侧后，即可实现还原

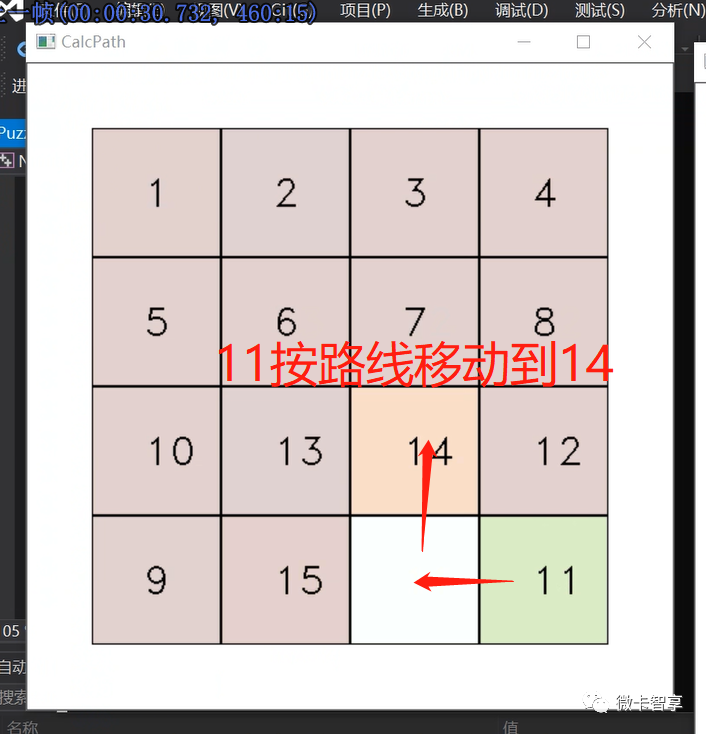
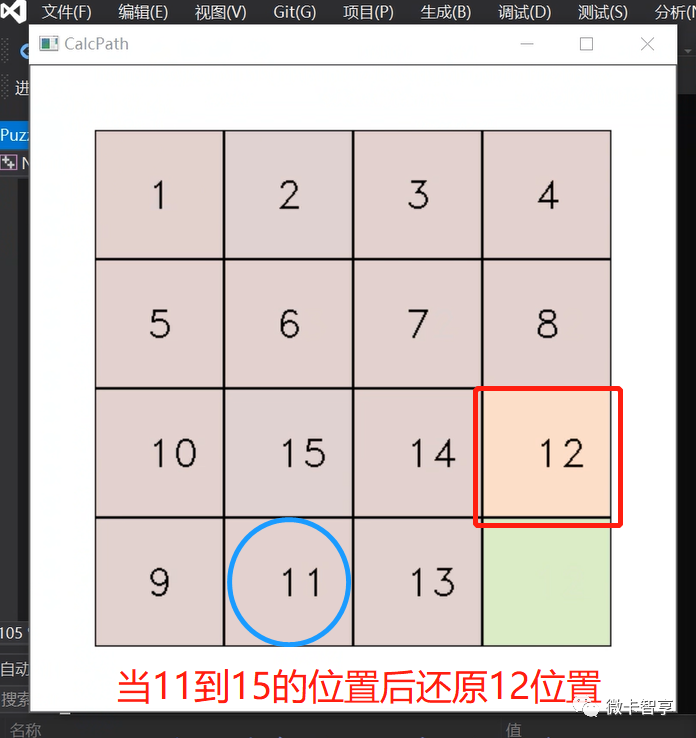
第三和第四行要一起处理，基本都是按上图上的方法将9和10，还有11和12移动到两侧，然后把13–15移动好后统一还原即可。这两天基本就是固定套路，不过在还原（9，10）或是（11，12）时，有机率会出现下面的情况：

f49ad62bb32458c4178c05467e41f73b.png

移动一步后

6714958a269eadaf65bd235fe4bb37f8.png

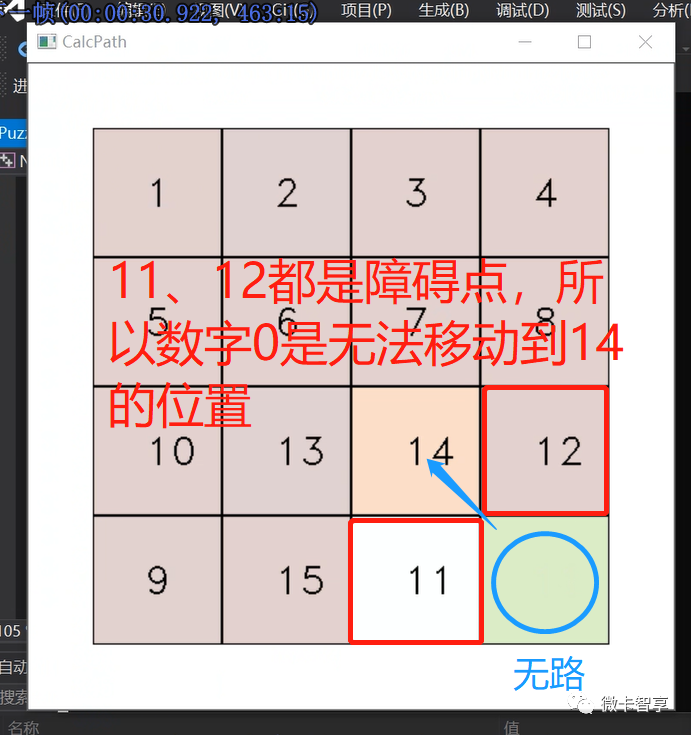
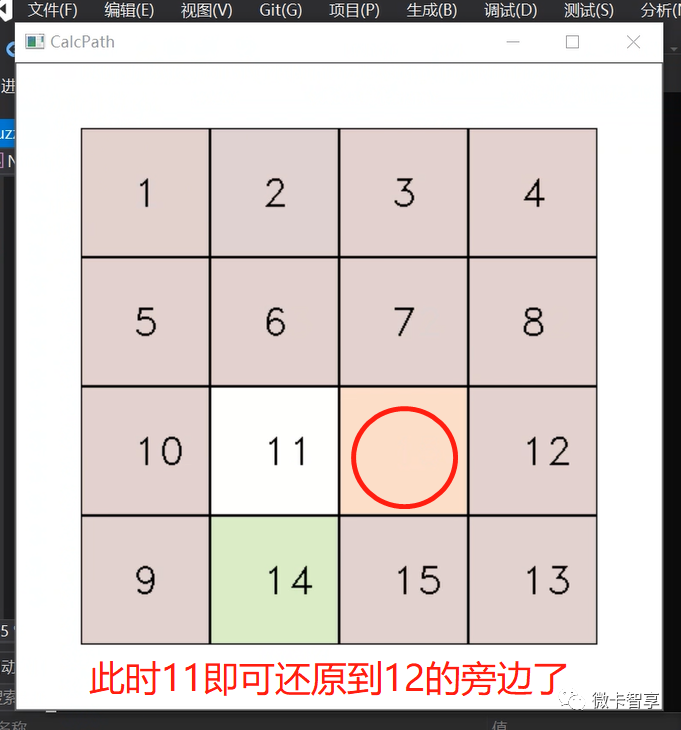
当遇到上面这种情况时，也算进入了异常处理，需要将12的障碍点先解锁，然后让11先移动到15的位置（因为在右下四个小格中，无论怎么转也不会出现我们要还源的11在12的上面这样情况）

8968e6be8577f6660b3d1f3085b32420.png

6cdc55c81999eec1662ced016c923edf.png

cf16627c3a0aa163bf6285f409e11fbc.png

08a00891263f0b6a22dce98329877158.png

按上面的步骤，就可以把11和12的位置按到最右侧了，同理，9和10在排到左侧时有机率也会出现这样的情况，处理的方式和上面的是一样的。

处理异常函数

//处理11和12的异常
void Puzzles4x4::DealElevenTwelve(vector<vector<int>>& vts, vector<vector<int>>& sites)
{
  if ((vts[2][3] == 12) && (vts[2][2] = 11)) {
    //1.锁定11个12当前位置,然后将0移动到右下角
    sites[2][2] = 1;
    sites[2][3] = 1;
    pair<int, int> endPos(3, 3);
    ZeroMove(vts, sites, endPos, DirectFirst::Right);


    //2.解锁11个12的位置，将0移动到第三行第三个
    sites[2][2] = 0;
    sites[2][3] = 0;
    endPos.first = 2;
    endPos.second = 2;
    ZeroMove(vts, sites, endPos, DirectFirst::Up);
  }
}


//处理9和10的异常
void Puzzles4x4::DealNineTen(vector<vector<int>>& vts, vector<vector<int>>& sites)
{
  if ((vts[2][0] == 9) && (vts[2][1] = 10)) {
    //1.锁定9个10当前位置,然后将0移动到左下角
    sites[2][0] = 1;
    sites[2][1] = 1;
    pair<int, int> endPos(3, 0);
    ZeroMove(vts, sites, endPos, DirectFirst::Left);


    //2.解锁9个10的位置，将0移动到第三行第二个
    sites[2][0] = 0;
    sites[2][1] = 0;
    endPos.first = 2;
    endPos.second = 1;
    ZeroMove(vts, sites, endPos, DirectFirst::Up);
  }
}

最后就是所以有数字都还原的固定走法了，感兴趣的朋友可以下载源码查看，这里就不再列出来了。

03

还原总的处理时间

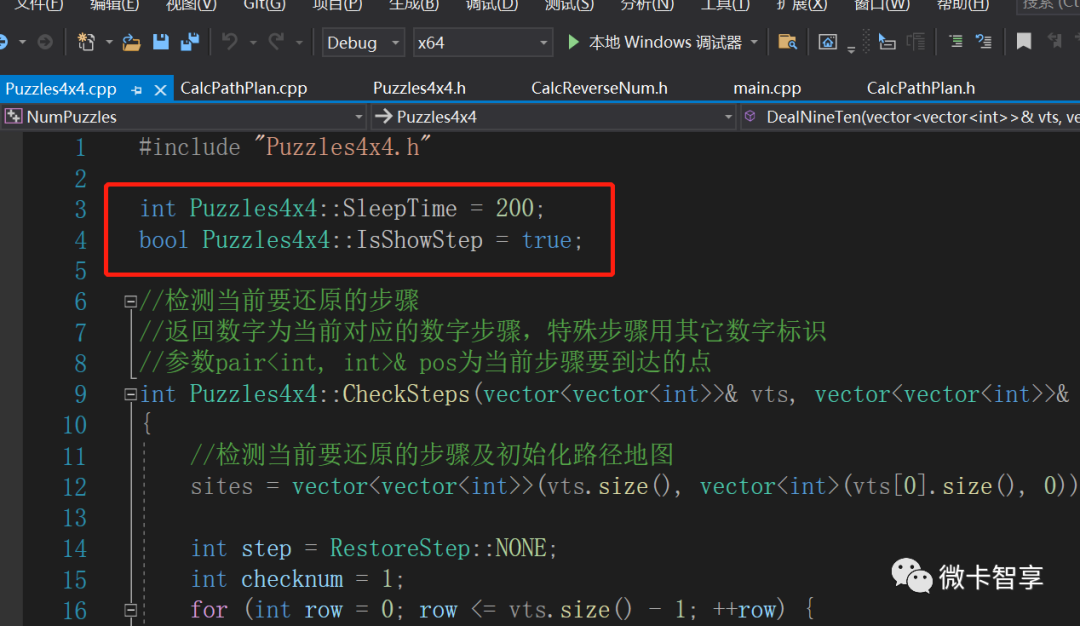
为了大家观看实现的方式，视频中我加入了展示移动效果，并在每一步显示后加入了200毫秒延时。

80b2b6a4ea5b8f9a9ed893e8fa95fba9.png

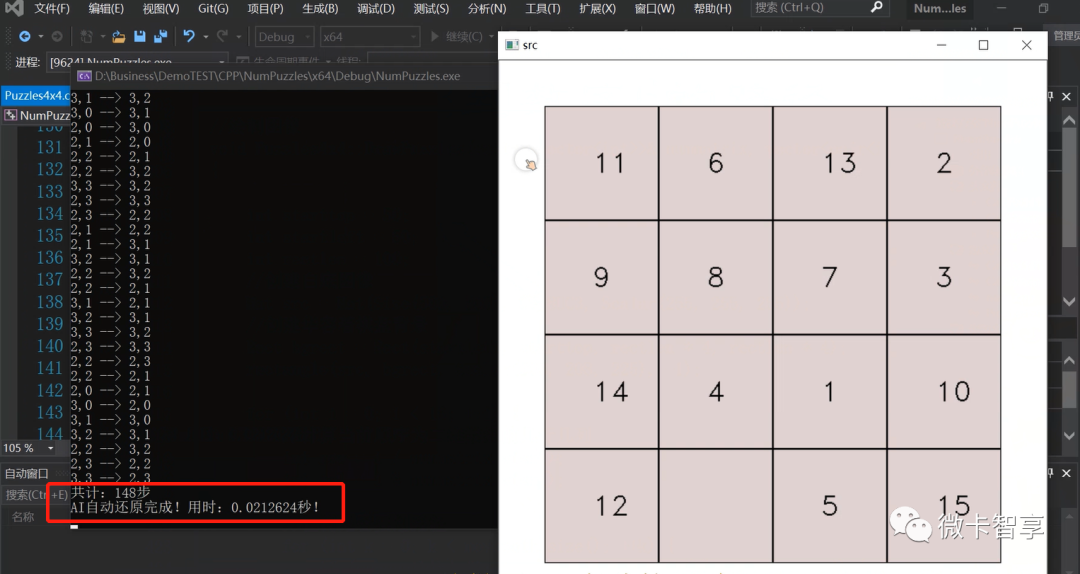
上图中IsShowStep的值为true，现在把它改为false后，关闭图像展示，经过多次测试，平均还原的速度在0.05秒内，速度还是挺快的。

6c01c1e855004b9b0fb522107f0e3528.png

b749cd02a2dddad2d72d85952b569fe9.png

64777c1dd5ef01a2c10b5c5297f1cc48.png

32eadf3e2b869b4f7082e2daf21f8599.png

华容道AI自动还原的方法就讲到这里了，最后来放一下源码地址。

源码地址

https://github.com/Vaccae/OpenCVNumPuzzles.git

GitHub上不去的朋友，可以击下方的原文链接跳转到码云的地址，关注【微卡智享】公众号，回复【源码】可以下载我的所有开源项目。

完

d39363d2114180df1c17fce4d9a0d817.png

扫描二维码

获取更多精彩

微卡智享

1a9ef2254169565571eb10b2acd072c6.png

「 往期文章 」

整活！我是如何用OpenCV做了数字华容道游戏！（附源码）

C++ OpenCV去燥函数fastNlMeansDenoising的使用

C++ OpenCV实现图像去阴影

 

今天的文章趣玩算法–OpenCV华容道AI自动解题分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/67267.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注