几何光学学习笔记（19）- 5.2光学系统的孔径光阑、入射光瞳和出射光瞳

5.2光学系统的孔径光阑、入射光瞳和出射光瞳

1.孔径光阑、入射光瞳和出射光瞳

光学零件的直径是有一定大小的，不可能让任意大的光束通过，而实际光学系统总是对一定孔径的光束成像。因此，必须有一个光孔(可能是一个透镜框，也可能是一个专门设置的光阑)限制着光束的大小。这个光孔就叫做孔径光阑。

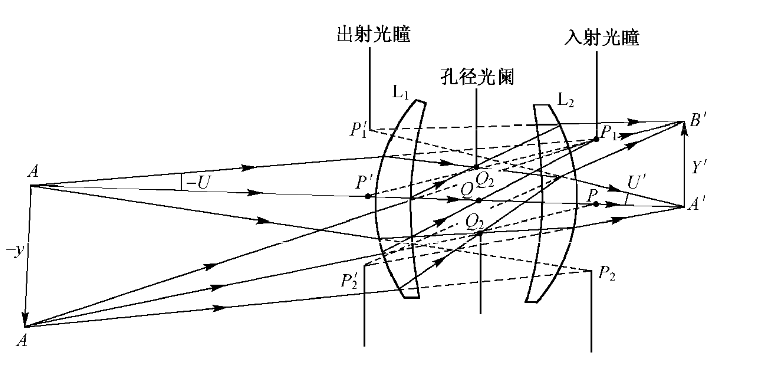
孔径光阑通过其前面的透镜成像到物空间去，其像决定了光学系统的物方孔径角，就形成了入射光瞳$P_{1}P{P}_2$，简称入瞳；孔径光阑通过其后面的透镜成像到像空间去，其像决定了光学系统的像方孔径角，就形成了出射光瞳$P_1^{\prime }{P}^{\prime }{P}_2^{\prime }$，简称出瞳；

显然，入射光瞳通过整个光学系统所成的像就是出射光瞳，二者对整个光学系统是共辄的。如果光阑在整个系统的像壁间，那么它本身也是出射光瞳。反之，在物空间，它就是入射光瞳。

使所有的光学零件的通光孔通过其前面的光学零件成像到物空间去，则出射
光瞳对物面中心的张角最小，此即像方孔径角 U。
使所有的光学零件的通光孔通过其后面的光学零件成像到像空间去，则出射
光瞳对像面中心的张角最小，此即像方孔径角 U’。

由物面中心通过入射光瞌边缘的光线常称为第一辅助光线。

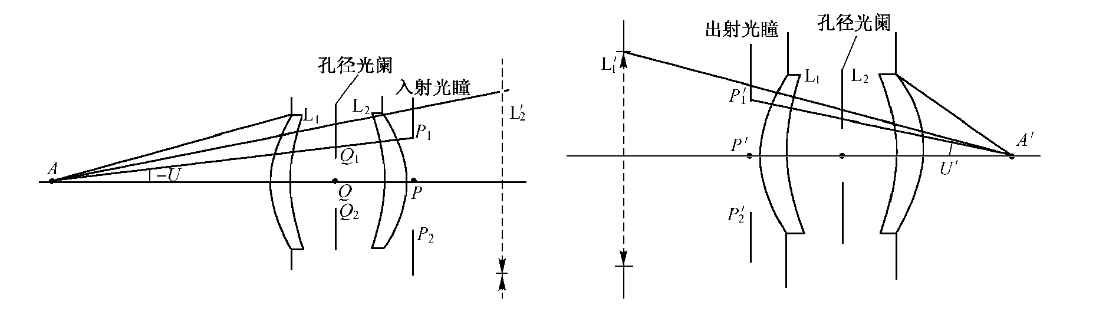
如果透镜L1和 L2完全相同，并对称于光阑放置，则其入射光瞳和出射光瞳的大小和倒正完全一样，即入射光瞳和出射光瞳之间的垂轴放大率为+1。因而结构对称于光阑的对称式系统入射光瞳和出射光瞳与光学系统的物方主面和像方主面相重合。

2.孔径光阑、入射光瞳和出射光瞳之间的关系，主光线

通过入射光瞳中心的光线称为主光线。对于理想光学系统，主光线也必然通过孔径光阑和出射光瞳中心。主光线是物面上发出充满光学系统入射光瞳的成像光束的轴线。

由物方视场边缘发出通过入射光瞳中心的近轴光线，称为第二近轴光线。因为近轴光计算具有理想光学系统计算的性质，故其必然通过孔径光阑中心和出射光瞳中心。由出射光瞳射出后的光线和高斯像平面的交点的高度为理想像高。

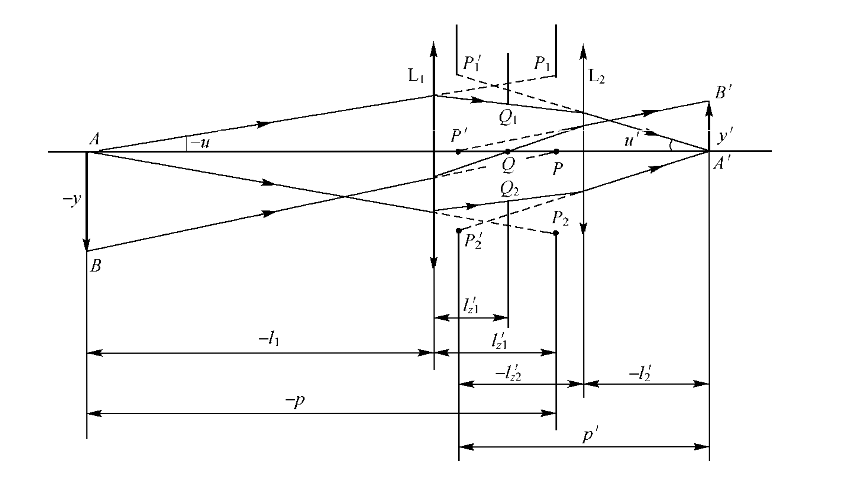
用高斯公式可以方便地导出入射光瞳相对于第一光组(前组)的距离 ：
$$l_{z1}=\frac{l_{z1}^{\prime }{f}_1^{\prime }}{f_1^{\prime }-l_{z1}^{\prime }}$$
孔径光阑到第二光组的距离为：
$$l_{z2}=l_{z1}^{\prime }-d$$
同理可以得出射光瞳到第二光组（后组）的位置 ：
$$l_{z2}^{\prime }=\frac{l_{z2}^{\prime }{f}_2^{\prime }}{f_2^{\prime }-l_{z2}^{\prime }}$$
$f_1^{\prime }和f_2^{\prime }$分别为第一光组和第二光组的像方焦距。

入射光瞳和光阑间的垂轴放大率为：
$$b_{z1}=\frac{D_A}{D}$$
$D_A为孔径光阑的直径，D为入射光瞳的直径。$

孔径光阑和出射光瞳间的垂轴放大率为：
$$b_{z2}=\frac{D^{\prime }}{D_A}$$
$D^{\prime }为出射光瞳的直径。$

入射光瞳和出射光瞳间的垂轴放大率为：
$$b_z=b_{z1}{b}_{z2}=\frac{D^{\prime }}{D}$$

己知入射光瞳和出射光瞳的直径，可分别求出物方和像方的孔径角，即：
$$u=\frac{D}{2p}=\frac{D}{2(l_1-l_{z1})}$$

$$u^{\prime }=\frac{D^{\prime }}{2p^{\prime }}=\frac{D^{\prime }}{2(l_2^{\prime }-l_{z2}^{\prime })}$$

入射光瞌直径D和整个系统焦距 f’之比称为该系统的相对孔径，即:
$$\frac{D}{f^{\prime }}=\frac{1}{K}$$
式中，K为光瞳数或者焦距数，常称为F数：
$$K=\frac{f^{\prime }}{D}$$
当物体在很近的距离时，常用物方孔径角正弦和物空间介质折射率的乘积来取代相对孔径，称为数值孔径，常以NA 表示，即:
$$NA=n_{1}sin{U}_1$$
相对孔径(或光瞳数)和数值孔径都表示了光学系统的光学特性。

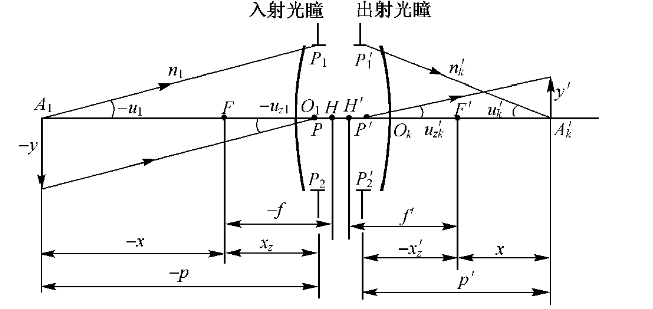
3.以光瞳中心为坐标原点的物像关系

$$\frac{b_z}{p^{\prime }}-\frac{1}{p}\frac{n_1}{n_k^{\prime }}\frac{1}{b_z}=\frac{1}{f^{\prime }}$$

这就是以入射光瞌中心为坐标原点的物像位置关系公式，或称为以光睡中心为坐标原点的高斯公式。

如果光学系统处于同一介质中，叫$n_1=n_k^{\prime }$ ，光学系统对称于光阑，即对称式物镜，则主面和光瞳平面重合，有$b_z=1$ ，则$x_z=-x_z^{\prime }=-f=f^{\prime }$。

则$p=l,p^{\prime }=l^{\prime }$,上式即成为一般的高斯公式。

光瞳处的拉赫不变量：
$$n_1{h}_z{u}_{z1}=n_k^{\prime }{h}_z^{\prime }{u}_{zk}^{\prime }=J_z$$
式中，$h_z和h_z^{\prime }$ 为第一近轴光线与入射光瞳和出射光瞳平面相交的高度；$u_z和u_{zk}^{\prime }$分别为第二近轴光线在物像空间和光轴的夹角。

今天的文章几何光学学习笔记（19）- 5.2光学系统的孔径光阑、入射光瞳和出射光瞳分享到此就结束了，感谢您的阅读。