udacity-谷歌自动驾驶-课程笔记-localization

前言：由于车辆gps的误差基本在2-10米，而自动驾驶时这些误差时不可接受的，所以需要利用车身传感器等信息辅助判断车辆位置，而谷歌这套模型可以使定位误差偏移在10厘米左右。

一、离散一维世界的定位

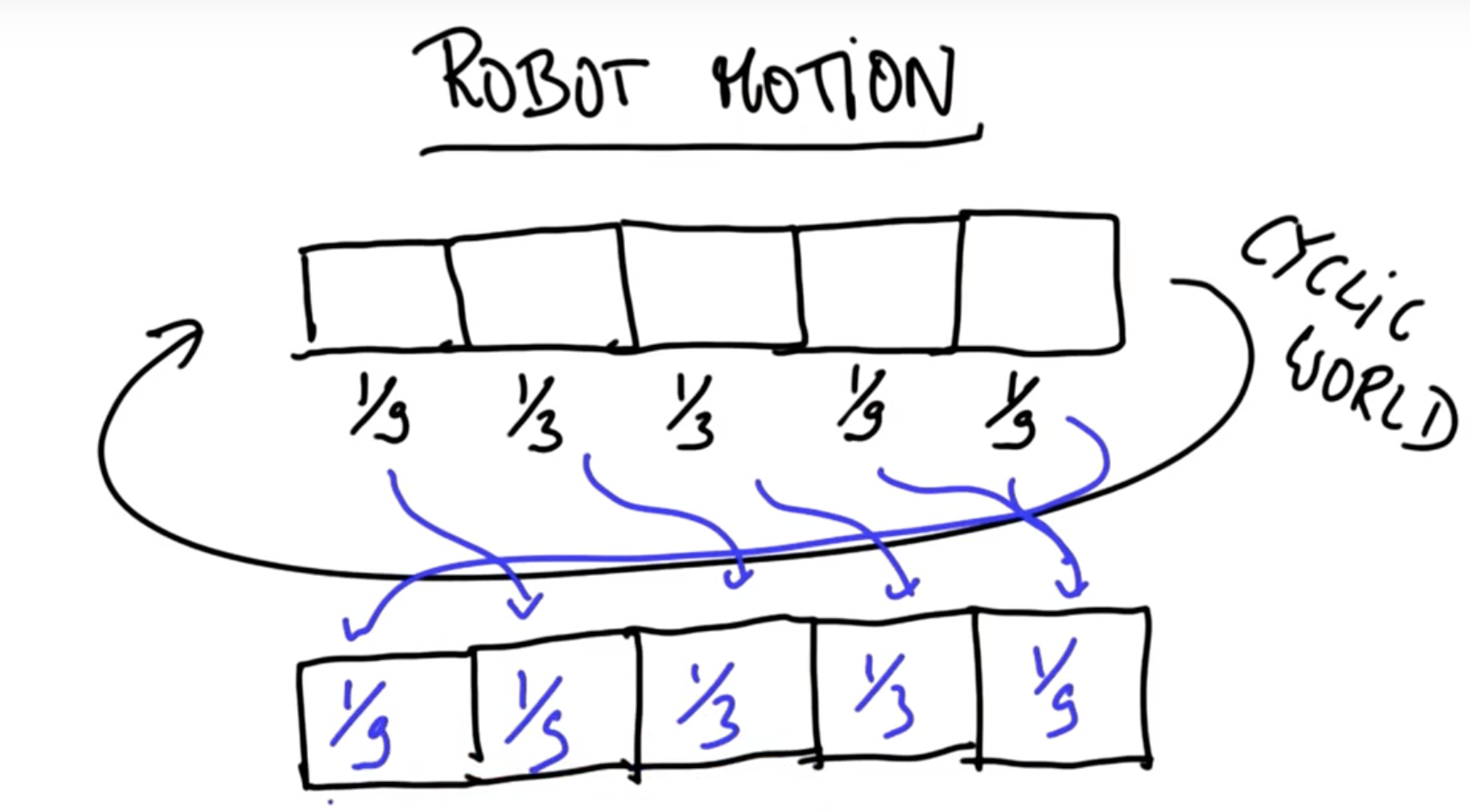
先用离散一维循环世界的定位来说明整体的定位原理（x8的后面是x1）
1、例如：假如这个一维世界共有n个格子，每个格子都是一样的，则车在任何一格的概率是相同的，所以整体的概率分布如下：

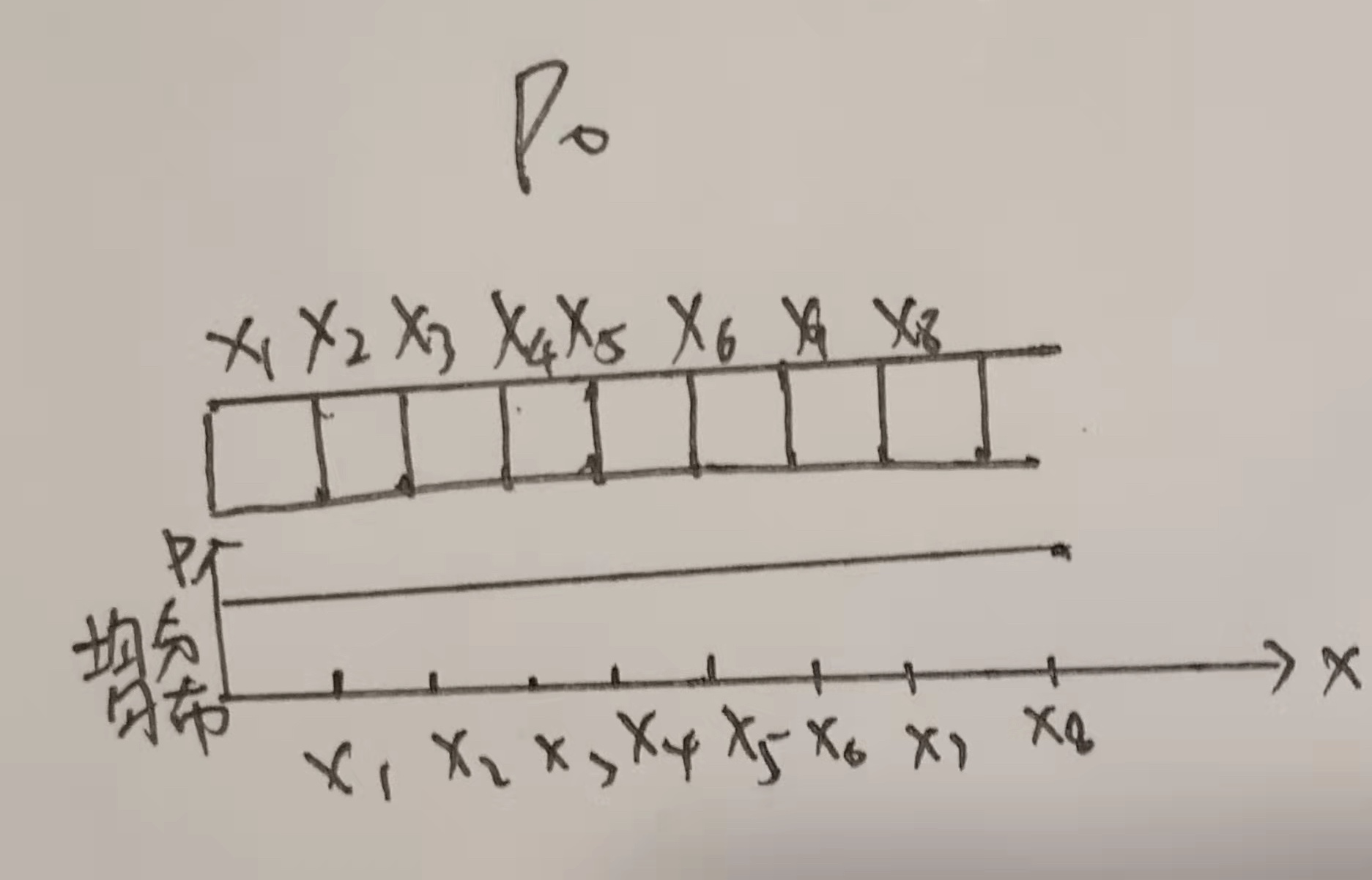
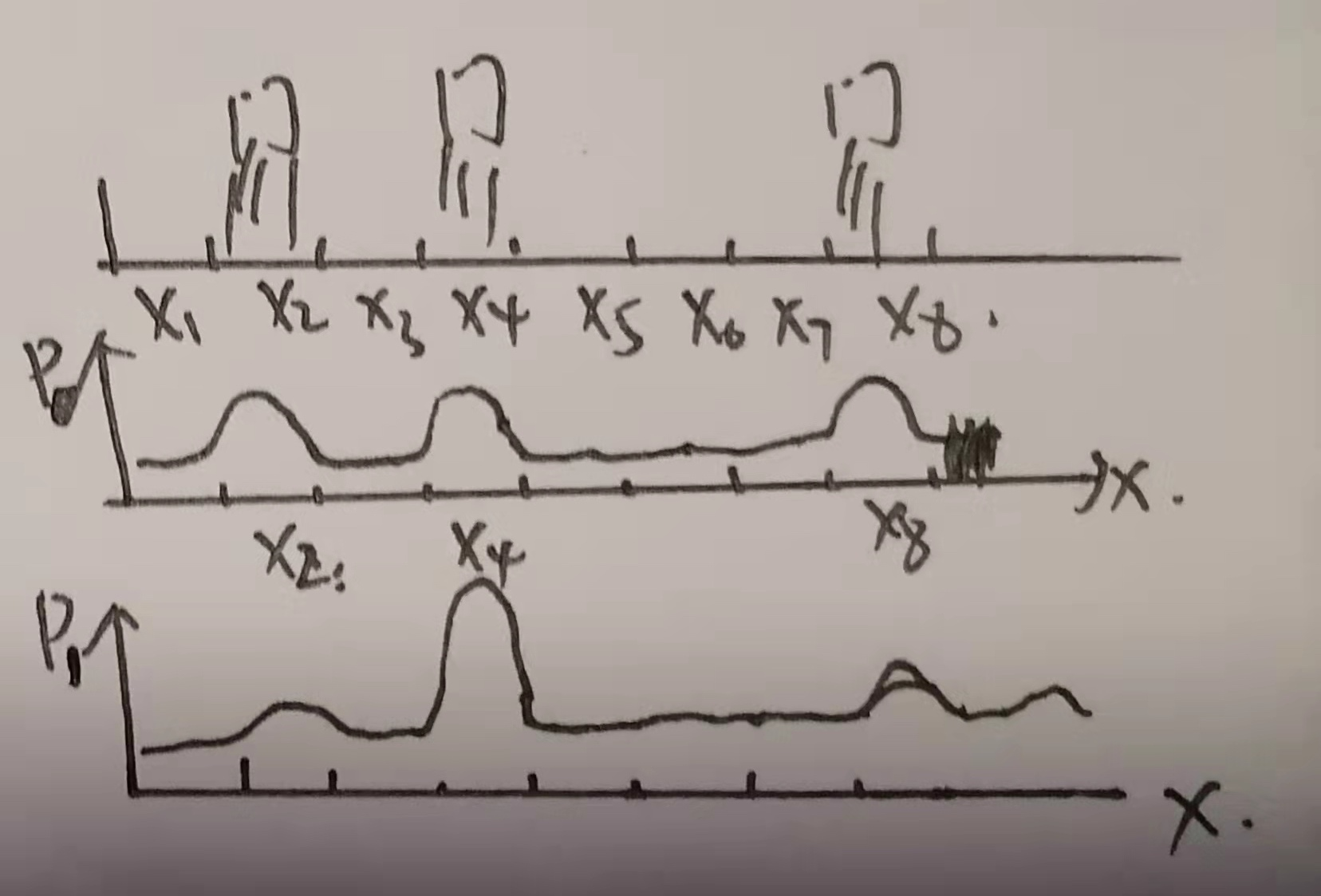
2、当这个一维世界出现不同，且车辆上存在传感器可以感知到不同时，那么车辆停驻位置可以有所不同。例如：x2、x4和x8处出现了小门，而车辆的传感器感知到小门，则小车停驻在x2、x4和x8处的概率大于其余各处的概率，分布如下图中P0（为啥其余各处不是0，因为模型要考虑传感器数据错误的情况）。但是此时我们还是无法判断小车在哪里，因为有三处的概率是相同的，当我们可以操纵小车移动，让小车移动后再感知一次可以得到差异，比如我们让车移动两格，再感知一次，如果再感知到门的存在，那我们可以得知车辆此时在x4的概率远远大于其他任何一处（因为两格前车辆在门处，移动两格还在门处，全世界只有x4这一个地方，为啥其他地方不是0，因为要考虑感知传感器误差和移动传感器误差等因素）

3、详细概率计算举例
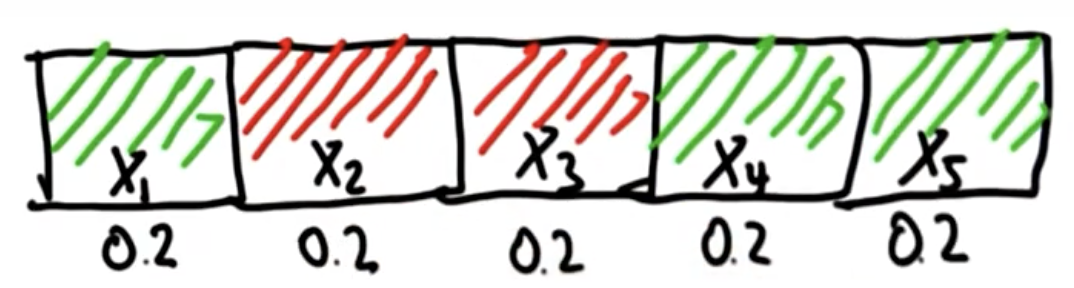
3-1、当世界实际分为5个格子，每个格子有自己的颜色，在没有任何信息的时候，则初始化车辆出现在每个格子的概率都是相同的，等于1/n，此处p(x_i) = 0.2

# 代码表示此世界
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']

3-2、当车辆感知到红色的时候，x2和x3的概率应该更大，剩余应该更小。

Z = 'red'
pHit = 0.6
pMiss = 0.2

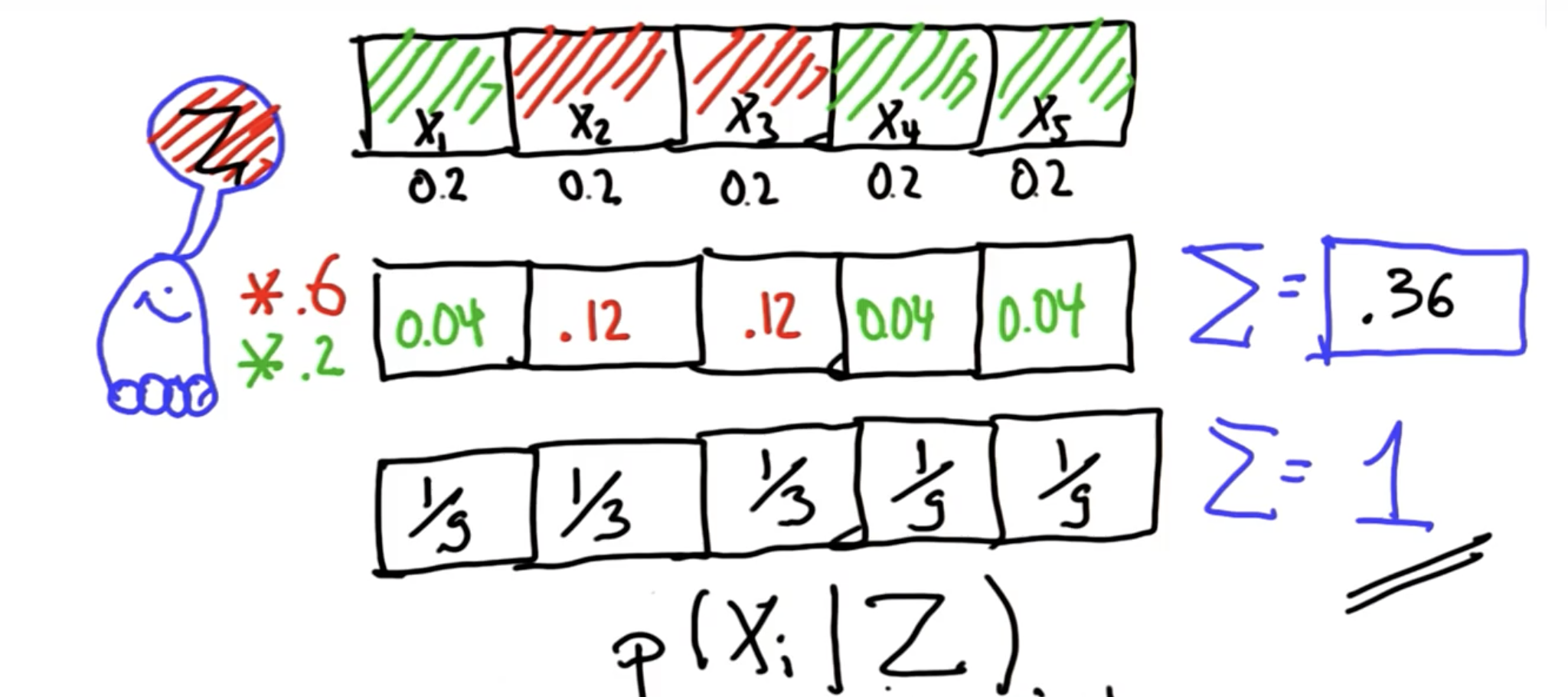
3-3、此时模型采用乘法，给红色格子（x2和x3）乘以更大的数字（0.6），给绿色格子乘以小一点的数字（0.2），实现差异化，最后再做一个归一化，得到条件概率：在检测结果为红色（事件z）的情况下，车辆在xi处的概率

3-4 基于一次感知结果，更新xi处的概率的函数如下：

def sense(p, Z):
    q=[]
    for i in range(len(p)):
        hit = (Z == world[i])
        q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
        
    sum_q = sum(q)
    for j in range(len(q)):
        q[j] = q[j]/sum_q
        
    return q

【插一句】
这里套用的贝叶斯公式是：P（xi|感知为红色） = P（感知为红色｜xi） P（xi）/P(感知为红色)
1、最开始我认为，传感器感知正确的概率理论上应该是等于1-感知错误的概率的，但是课程中用的是pHit和pMiss，说明实际情况中并不是感知正确和感知错误这样翻译的，这里只是为了方便理解这样记录了。而从贝叶斯公式的角度理解这个问题，pHit和pMiss对应的是：P（感知为红色｜在xi处）这一项，那么这一项就应该是先验概率了，即pHit应该是在x2和x3处感知为红色的概率，而pMiss为在x1、x4和x5处感知为红色的概率，从这个角度理解的话，两个概率确实没有直接关系。
2、其实这里的归一化过程是简化了贝叶斯公式中P(感知为红色)的计算，理论上这里应该使用全概率公式计算P(感知为红色) ，也就是各个xi 感知为红色的概率 P（xi）的概率和 ，算下来也是0.36

3-5、我们再把车辆移动的情况加进来。理论上车子向前移动一步，则带着原概率都向前移动一步，因为是循环世界，最后的概率移动到最前面，课程图片很好的解释了过程：

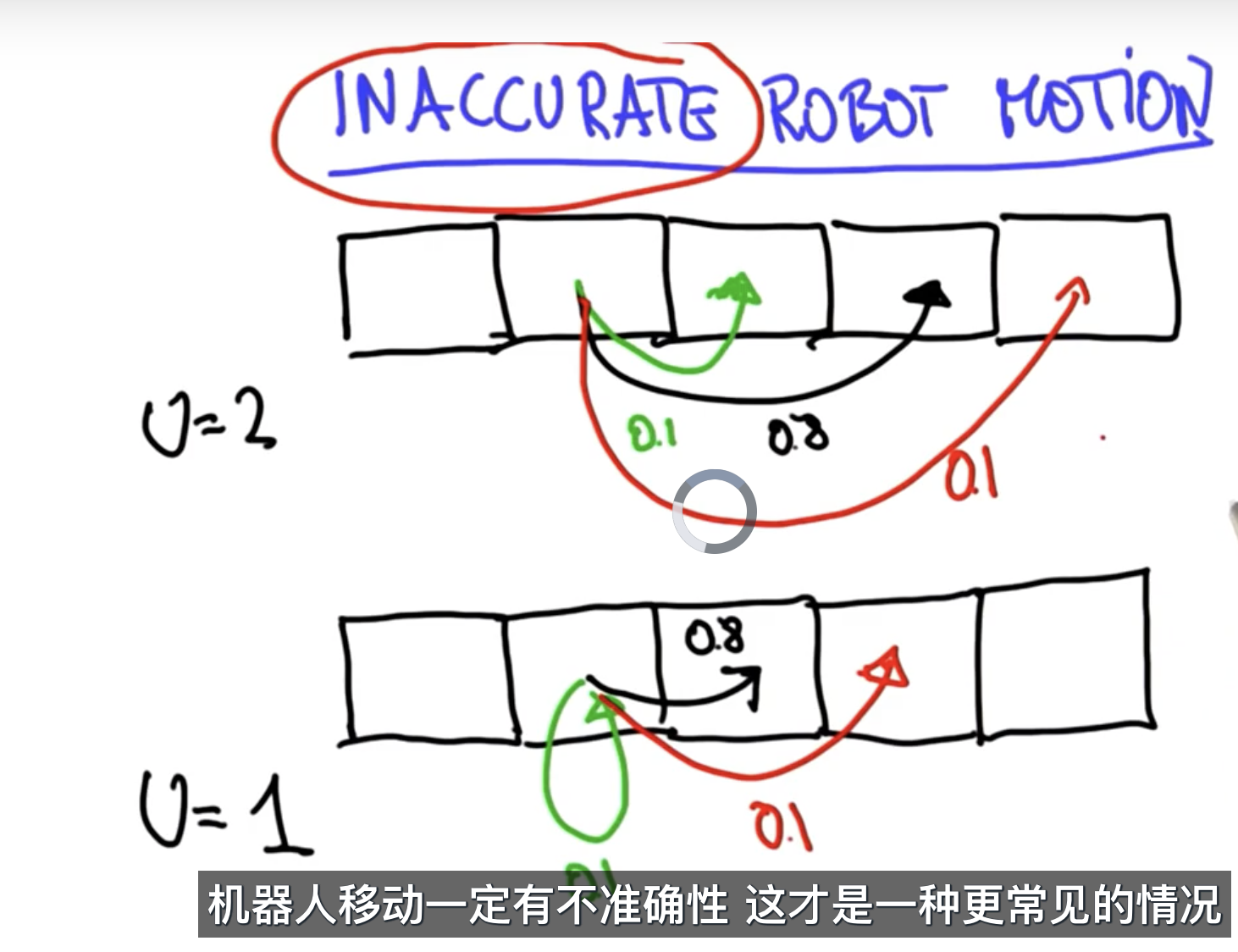
但是为了考虑移动误差，即车辆移动不正确的情况，课程中考虑车辆存在向前移动多一步和少一步的情况，移动正确的概率是0.8，多一步和少一步的概率分别是0.1，所以移动的计算过程可以理解为变成了一个卷积的过程，移动n步后，P(xi)= P（xi – n-1）*0.1 +P（xi – n）*0.8 +P（xi – n+1）*0.1

P(move) = [0.1,0.8,0.1]

def move(p, U):
    q = []
    
    for i in range(len(p)):
        j =  (i-U)%len(p)
        q.append(p[j]*pExact + p[(j-1)%len(p)] * pOvershoot + p[(j+1)%len(p)] * pUndershoot )

【后续】
1、课程中其实对公式的解释并不是特别多，因为更侧重编程实现，其他地方很多对贝叶斯的举例，可以参考。但是个人感觉，贝叶斯公式还是很简单的，然而在实际应用中，公式右边的概率基本是都是要先基于离线数据统计出来的，也就是贝叶斯分析过程，感觉这个过程其实是会比较困难的，之前看到过一个很有意思的说法：

贝叶斯的数学计算主要考察对条件概率的实用。 但是有时候我们也不理解条件概率， 比如著名的辛普森案， 为了证明辛普森有杀妻之罪，检方说辛普森之前家暴的历史，而辩护律师说，美国有400万女性被丈夫或男友打过，而其中只有1432人被杀，概率是2800分之一。 这其实就是误用了条件概率， 因为辩护律师用的条件是家暴，用来推测的事件是男友杀人， 而事实上这里的条件是被杀而且有家暴，而要推测的事件是凶手是男友（事实上概率高达90%），这才是贝叶斯分析的正当用法， 而辩护律师却把完全在混淆条件与要验证的假设。
作者：许铁-巡洋舰科技
链接：https://www.zhihu.com/question/51448623/answer/747656479
著作权归作者所有。

*这个实验特别有意思的地方在于2800分之一 表示的是一个人被家暴后被杀的概率，它很容易让人误解为：概率说明被家暴和被杀的是两码事，所以被杀的话和家暴没什么关系，不能由此推断凶手就是男友，然而其实应该要使用家暴&被杀，极速那凶手是男友的概率
2、课程中说到另一个很有意思的事情，如果我们已经车辆位置，然后只做移动，不做观测，无限次之后车辆回归到均匀分布状态。
每次观测之后，我们能得到更加明确的结果，而移动之后却得到更模糊的结果

今天的文章udacity-谷歌自动驾驶-课程笔记-localization分享到此就结束了，感谢您的阅读。