《编码》读书笔记
二 如何制作加法器
前言
书接上回,看小将与或门,长驱直入,在长坂坡杀了个七进七出。hold on,hold on…
半加器
上一次,我再解释异或门的时候,我借助了二进制的加法口诀,将二进制加法分成两部分,一是加法位计算,二是进位计算。加法位计算我们就可以用异或门表示,进位计算我们可以用与门来表示。将两个原件组合成来计算加法:
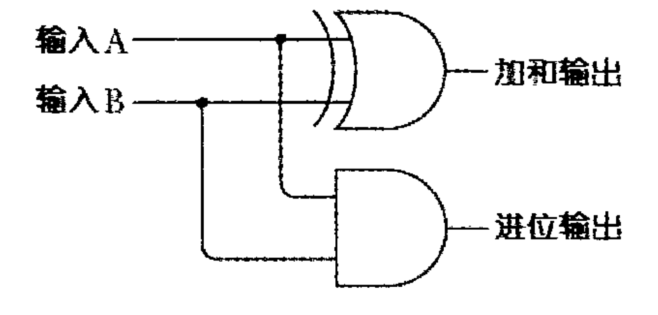
将这样的组合就是一个半加器(Half Adder),我们把这个组合,进行抽象。如下:
为啥叫加半加器呢?因为他不完整,你不能说东厂的厂公他是一个顶天立地的男人。我们仔细看这个半加器,当我们计算一个 101 + 101 的时候,第一位的计算,输入 1 和 1,加和为 0,进位为 1;第二位计算,输入两个 0,但是第一位计算的进位没有输入到半加器中。他不能完整的计算加法。
如何设置一个全加器?
- 首先第一个半加器的和必须和前一列计算的进位相加,输入到第二个半加器;
- 第二个班加器计算和是,是计算的结果;进位与第一次进位通过或门得到进位;
- 两个半加器的进位,没有都是1可能,所以只需要一个或门即可,不需再加一个全加器。
再次抽象!我们把上边组合进行合体,我们得到了全加葫芦小金刚:
| 输入A | 输入B | 进位输入 | 加和输出 | 进位输出 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
将这个表带入上边的半加器组合成的全加器,走几个输入。
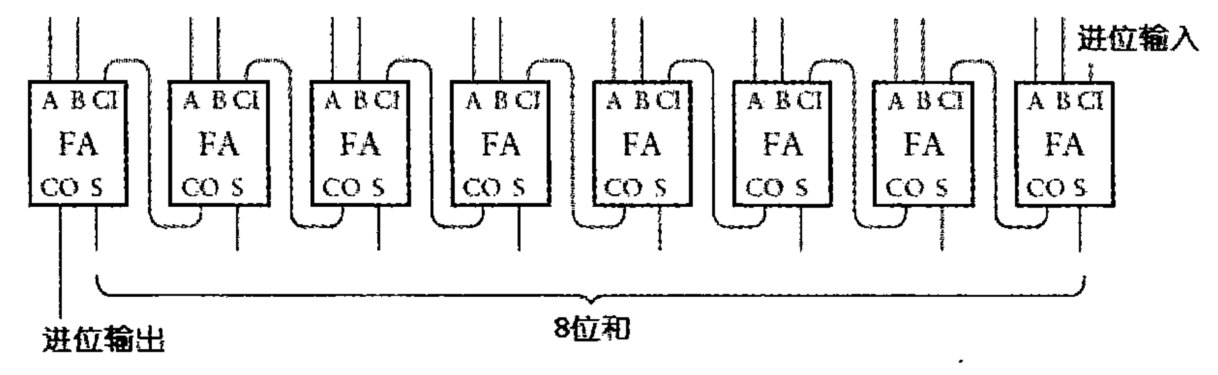
构建一个8位加法器
我们有了上边的加法器,我们就能构建一个8位的二进制加法器。
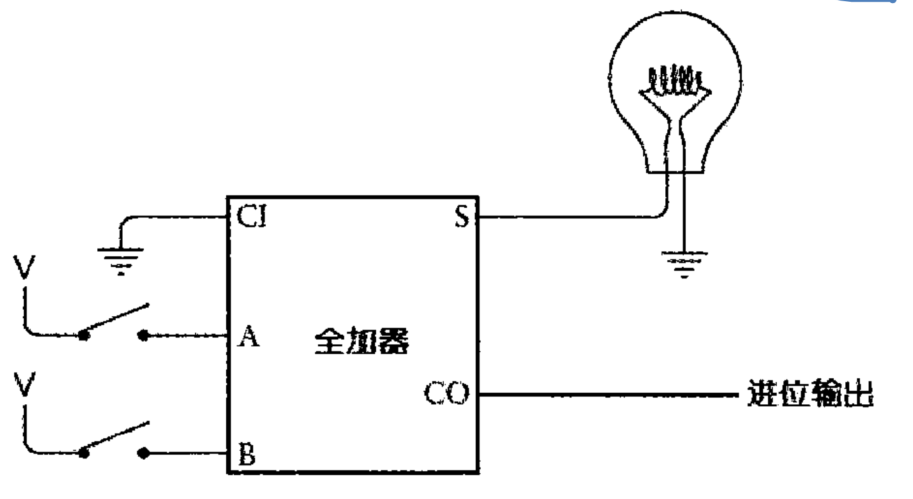
- 首先在计算第列的时候,我们需要把第一个全加器的加和结果链接灯泡;
- 全加的器的进位输入到下一列计算用的全加器中;
- 输入A,输入B,我们接入第一位的计算的两加数;
- 第一列计算是没有进位输入的,所以在全加器进位输入,我们直接输入 0。
做好第一列,后边的都明明白白的了。
-
前一列的进位,接入全加器的进位输入;
-
计算的加数,接入A,B;
-
加和接入灯泡;
-
进位输出接入下一列全加器的进位输入中。
只有最后列需要计算结果需要接入两个灯泡。最后我们就构建出一个计算8位加法器。
然后我们买个硬点的塑料盒子,把这个加法器进行包装一下,合成8位加法器,就可以摆摊售卖了。
铁匠林纳斯:对你的8位加法投来羡慕的眼光。
ps:DNF的npc铁匠林纳斯,和Linux的爸爸是相同的名字。
当然了,我们有了8位加法器了,我们马上就能构建我们 32768 位加法计算器了。我们只需要 4096个8位的加法器就可以了。
总结:
我们从与或门和与门构建起来了一个半加器;我们又通过两个半加器和一个或门构建起来全加器。再通过全加器的串联我们构建起来了一个8位加法器。
我们重要的是理解思想,硬件的构成,也是通过一个个小原件,构建一个大原件,然后组合成一个能有实际效果或是实际作用的组件。硬件的思想也有抽象和封装的思想。软件编程过程或是学习过程中,也是随处可见这些思想。SpringCloud中各种组件也在满足条件中随意来回搭配。也是通过这些组件的搭配来构建一个完整高效的系统的。
今天的文章如何制作加法器 《编码》读书笔记 二分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/67818.html