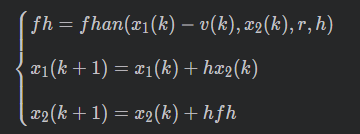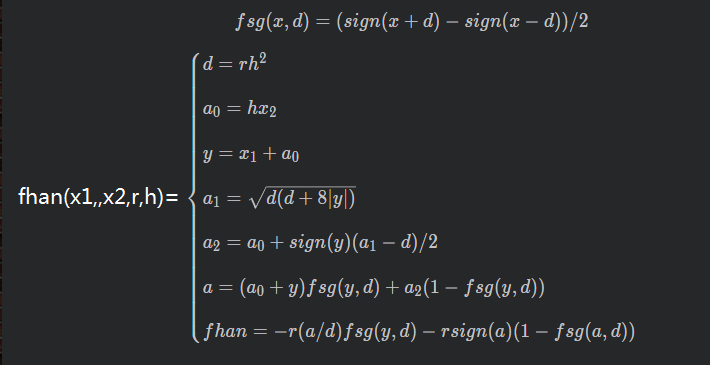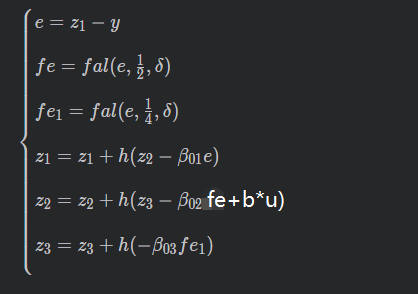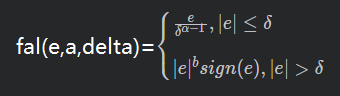ADRC自抗扰控制，有手就行

ADRC自抗扰控制，有手就行

  关于ADRC的优点本人不会赘述，毕竟作为一个ADRC算法都推导不出来的应用工程师，最希望看到的就是有手就行的操作方法。ARC的缺点就显而易见，就是参数多，一环ADRC大概就有11个参数，但一个粗略的效果很快就出来。本文所有的言论仅以我最近的一次速度闭环控制经验之谈，并没有经过大量的实验验证其绝对正确性，慎用（注：文中公式来自于csdn用户：遥远的乌托邦，有稍作修改）。
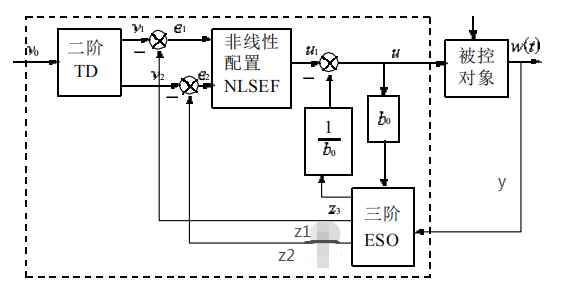
  ADRC说白了就是PID的升级版，保留了PID的优点，改良了PID的缺点，其结构和PID一样，ADRC可以被看作三个作用效果的结合，分别是TD（跟踪微分器）、ESO（扩张状态观测器）、NLSEF（非线性控制律）。TD是为了防止目标值突变而安排的过渡过程；ADRC的灵魂就在于ESO，其作用下文给客官细细道来；NLSEF是为了改良PID直接线性加权（输出=比例+积分+微分）的缺点而引进的非线性控制律，其更符合非线性系统。

  从上图看到TD只有输入v0（系统的目标值），其输出的v1为v0的过渡过程，例如v0原先是0，突然将v0改成10，那么v0就有个突变，而v1不会随v0突变，而是慢慢的爬升到v0，不会有静差也不会有超调，v1的爬升时间取决于TD参数（具体TD参数在下文给出并做解析）调整，也可以调整成跟随v0突变。v2是v1的导数，即v1的微分。
  其数学公式如下：

  上图中可以看出ESO的输入是有两项，一项是反馈值y，另一项是输出值u *b0（b0被称为系统系数）。输出则为z1、z2、z3；z1和z2是被称为系统的两个状态，z1的数值是跟随着输出y的，假若系统闭环成功的话，z1,、y、v1三个数值应该是一样的。z2是跟随y的微分的，加入系统闭环成功的话，z2、y的微分、v2三个数值应该是一样的。z3是系统扩张的一个状态，观测的是系统的总扰动，z3是自抗扰的灵魂所在。
  ESO数学公式：

  NLSEF输入是e1（e1=v1-z1）、e2（e2=v2-z2），其输出是u1，u1并没有叠加系统总扰动补偿，它只是NLSEF的输出，并不是系统的最终输出。系统最终的输出是直接作用到被控对象的量u（u=u-z3/b）。
  w（t）是假定的一个系统总扰动。
  NLSEF的数学公式有几种那么多，本人仅使用了第二种：

/******************ADRC program with C******************** // write by suitcalaw // copy by the high hand net world // https://blog.csdn.net/b457738242 **********************2020-12-07*************************/

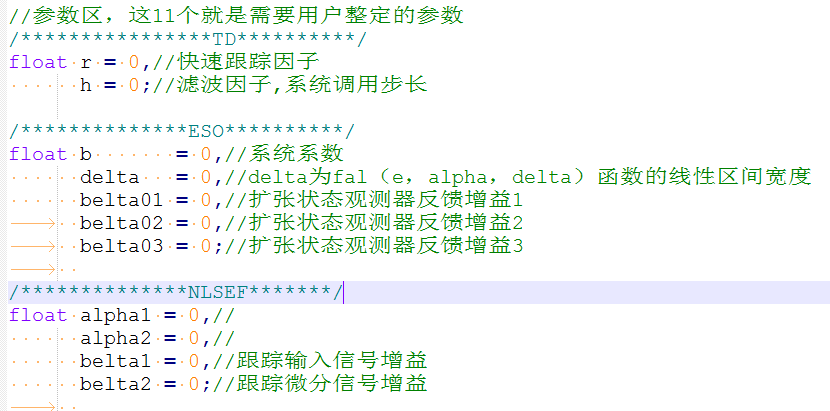
//参数区，这11个就是需要用户整定的参数
/****************TD**********/
float r = 0,//快速跟踪因子
      h = 0;//滤波因子,系统调用步长

/**************ESO**********/
float b       = 0,//系统系数
      delta   = 0,//delta为fal（e，alpha，delta）函数的线性区间宽度
      belta01 = 0,//扩张状态观测器反馈增益1
	  belta02 = 0,//扩张状态观测器反馈增益2
	  belta03 = 0;//扩张状态观测器反馈增益3
	  
/**************NLSEF*******/
float alpha1 = 0,//
      alpha2 = 0,//
      belta1 = 0,//跟踪输入信号增益
      belta2 = 0;//跟踪微分信号增益
	  
	  
/*****************************fhan函数*********************************/
float fhan(float x1,float x2,float r,float h)
{ 
   
 /*****************************第一套************************/
// float d = 0,
// a = 0,
// a0 = 0,
// a1 = 0,
// a2 = 0,
// y = 0,
// fhan = 0;
// 
// d = r*h*h;
// a0 = h*x2;
// y = x1+a0;
// a1 = sqrtf(d*(d+8*fabsf(y)));
// a2 = a0 + sign(y)*(a1 - d)/2.0;
// a = (a0+y)*(sign(y+d)-sign(y-d))/2.0 + a2*(1-(sign(y+d)-sign(y-d))/2.0);
// fhan = -r*(a/d)*(sign(y+d)-sign(y-d))/2.0 - r*sign(a)*(1-(sign(a+d)-sign(a-d))/2.0);
 /******************************第二套**********************/
	float deltaa  =0,
		  deltaa0 =0,
	      y       =0,
	      a0      =0,
	      a       =0,
	      fhan    =0;
	
	deltaa = r*h;
	deltaa0 = deltaa*h;
	y=x1+x2*h;
	a0 = sqrtf(deltaa*deltaa+8*r*fabsf(y));
	if(fabsf(y)<=deltaa0)
		a=x2+y/h;
	else
		a=x2+0.5*(a0-deltaa)*sign(y);
	if(fabsf(a)<=deltaa)
		fhan = -r*a/deltaa;
	else
		fhan = -r*sign(a);
	
  return fhan;
}
/************************************sign函数***************************/
float sign(float x)
{ 
   
	if(x>0)
		return 1;
	else if(x<0)
		return -1;
	else
		return 0;
}
/*******************************fal函数**********************************/
float fal(float e,float alpha,float delta)
{ 
   
  float result = 0,fabsf_e = 0;
  
  fabsf_e = fabsf(e);
  
  if(delta>=fabsf_e)
    result = e/powf(delta,1.0-alpha);
  else //if(delta<fabsf_e)
    result = powf(fabsf_e,alpha)*sign(e);
 
 return result;     
}
//中间变量区，不需要用户管理以及赋值
/****************TD*******************/
float x1 = 0,//跟踪输入
      x2 = 0,//跟踪输入的微分
/****************ESO******************/
      e  = 0,//误差
	  z1 = 0,//跟踪反馈值
	  z2 = 0,//跟踪反馈值的而微分
	  z3 = 0,//跟踪系统的扰动（总扰动）
/**************NLSEF******************/
      u = 0;//输出值
/********************************ADRC************************************/
float ADRC(float v,float y)  // 参数：v：输入的目标值； y：反馈值
{ 
   
  float u0 = 0,
        e1 = 0,
		e2 = 0;
/******************************TD****************************************/
  x1 = x1 + h*x2;
  x2 = x2 + h*fhan(x1-v,x2,r,h);
/******************************ESO***************************************/
  e = z1 - y;
  z1 = z1 + h*(z2-belta01*e);
  z2 = z2 + h*(z3-belta02*fal(e,0.5,delta)+b*u);
  z3 = z3 + h*(-belta03*fal(e,0.25,delta));
/******************限幅，ADRC正常的话不会达到限幅条件********************/
  if(z1>=30000) z1=30000;
  if(z1<=-30000) z1 = -30000;
  if(z2>=30000) z2=30000;
  if(z2<=-30000) z2 = -30000;
  if(z3>=30000) z3=30000;
  if(z3<=-30000) z3 = -30000;
/******************************NLSEF*************************************/
  e1 = x1 - z1;
  e2 = x2 - z2;
  
  u0 = belta1*fal(e1,alpha1,delta) + belta2*fal(e2,alpha2,delta);//其中0<alpha1<1<alpha2
  
  u = u0 - z3/b;
  
  return u;
}

  代码是根据上面的公式直接撸过来的，下图是ADRC的11个参数，就是我们需要整定的参数了。

  参数整定的规律是先将TD参数整定好，再整定ESO和NLSEF。
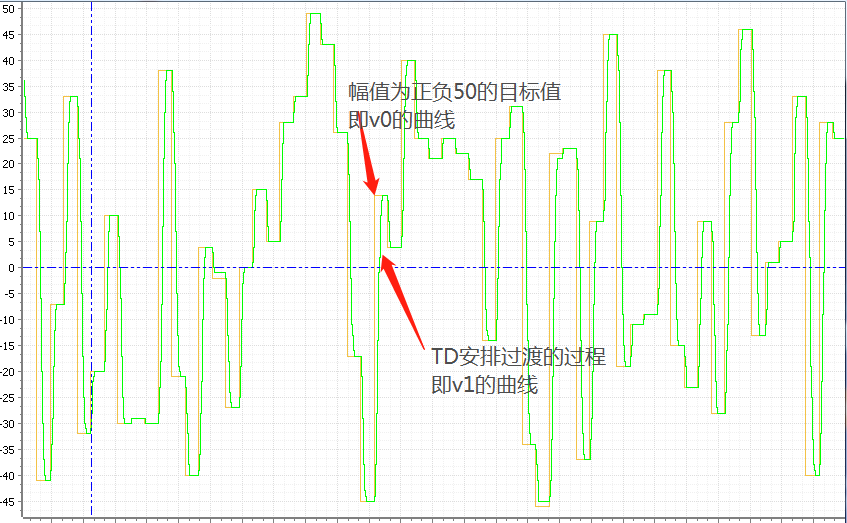
  TD的参数整定是最简单的，观测v1的输出和输入v0的线性，其跟随的快慢并没有规定一定要多快多慢，取决于你想要的效果。TD参数只有两个：快速因子r 和滤波因子h 。其中，r 与跟踪速度呈正相关，然而，随之带来的是噪声放大的副作用;h与滤波效果呈正相关，但当h增大时，跟踪信号的相位损失也会随之增加。滤波因子经常取值为ADRC控制周期，比如1ms调用一次，h就是0.001，这也不是死定的，可以根据自己的效果做细微调整。

  ESO共有b、delta、belta01、belta02、belta03共5个参数，其中delta取值范围在5h<=delta<=10h,h为ADRC控制周期。参数整定可以先将b定下来，比如取1或者2（最好还是能够知道你的二阶系统系数），然后先后调整belta01、belta02、belta03，观测z1能不能够很好的跟随反馈y，如果是，那么大概参数就调好了；如果不是，可以改动一下b，还是不行的话就得认认真真的检测一下反馈y是不是出了什么问题，比如变量数据类型转换有没有做好。如果懂得自己在输出中加入随机数（白噪声），注意幅值不能过大，观测一下z3是不是能够很好的观测到随机扰动。若以上两个条件都成立，那么ADRC就几乎被整定好了。
  NLSEF参数有alpha1，alpha2，belta1，belta2四个，其中0<alpha1<1<alpha2。belta1和belta2则视效果而定，通常ESO和NLSEF一起调，在整定ESO参数时，可以先把delta1和delta2定为1，再调ESO，待ESO有一定效果后，反复调整ESO参数无果，可以加入NLSEF参数整定，取得更好的效果。
  以上是本人的一次电机闭环ADRC的经历，其中曲曲折折，非自动化专业的我，跟着论文也推不出ADRC算法，只好这样先用着，效果也显著。我还是会继续修读自动控制原理，终有一天也会将ADRC算法推导明白，再细细分析。如有错误，也请见谅，如有侵犯，请联系修改。

今天的文章ADRC自抗扰控制，有手就行分享到此就结束了，感谢您的阅读。