算法谜题是一本经典算法谜题的合集。书中包括了一些古已有之的谜题,数学和计算机科学有一部分知识就发源于此。
pdf下载 资源分享汇总_nameofcsdn的博客-CSDN博客
目录
0 Guarini谜题
11 假币堆问题
12 平铺多米诺问题
14 复原国际象棋棋盘
16 煎饼制作
需要制作 n 个煎饼, 所用的煎锅一次只能同时煎两个煎饼。煎饼两面都需要烤, 完成一面的煎炸需要 1 分钟, 无论一次制作一个煎饼还是一次同时制作两个煎饼。设计一个算法计算做这项工作的最短时间, 并给出关于 n 的最短时间的计算方程。
17 国王的走位
对于(b),我解释一下具体是怎么算出来的
如果n是奇数,那么答案就是4*(1+3+5+…+n)=(n+1)^2
如果n是偶数,那么答案就是1+4*(2+4+6+…+n)=(n+1)^2
21 正方形的拆分
将一个正方形拆分成 n 个小正方形, 找出数字 n 的所有取值可能, 并且将这种拆分方法归纳成算法。
24 国际象棋棋盘着色问题
30 棍子切割
一根长度为 100 的棍子需要被切成 100 根长度为 1 的小段, 如果一次可以同时切割多根棍子, 问最少需要切几次? 设计一个算法, 处理此类问题, 即对于长度为n的棍子, 计算切割所需要的最少次数。
我的解答:
每次都把所有的棍子左端对齐,然后在最长的棍子中间的地方切。
假设答案为f(n),那么递推式为f(n)=f((n+1)/2)+1
由此可以求出通项公式f(n)=log2 n向上取整
34 星星的硬币
36 有限的差异
37 2n筹码问题
38 四格骨牌平铺问题
44 孰轻孰重
62 硬币收集
63 加减归零
66 留下的数字
70 跳跃成对1
有 n 枚硬币排成一排。目标是通过一系列的移动操作形成 n / 2 个硬币对 (两枚硬币摞成一摞)。每次移动操作可以操纵一枚硬币向左或向右跳过两枚与它相邻的硬币 (两枚单独的硬币或已经摞在一起的硬币对), 落在接下来的硬币上, 形成一摞,不允许三枚硬币摞在一起。相邻硬币之间的距离不管多远都可以忽略不计。求使问题有解的 n 的取值范围, 并设计一个算法, 计算最少需要移动多少次。
71 标记方格1
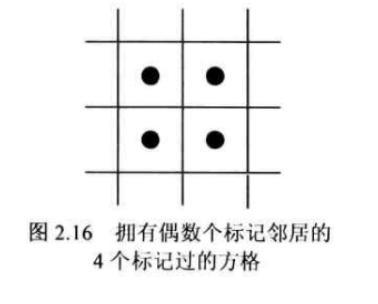
在一张无限大的方格纸上标记 n 个方格, 使得每个所标记的方格都拥有正偶数个标记过的邻居。邻居关系指的是水平或坚直方向上两个紧挨的方格, 对角线方向上的不算。所有标记的方格必须形成一个连续的区域, 即区域内任意两点之间都可以找到一条由相邻的方格所形成的路径。如图 2.16 所示就是 n=4 时的答案。问 n 怎样取值才能使本题有解?
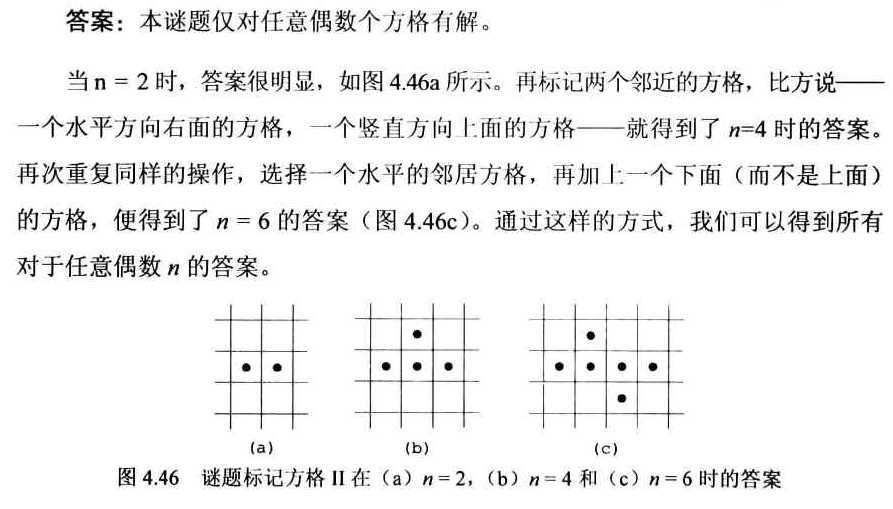
72 标记方格2
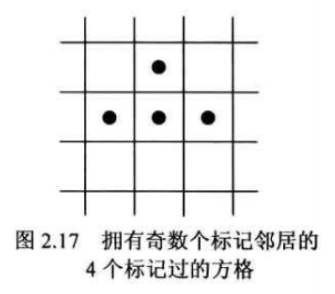
在一张无限大的方格纸上标记 n 个方格, 使得每个所标记的方格都拥有正奇数个标记过的邻居。邻居关系指的是水平或坚直方向上两个紧挨的方格, 对角线方向上的不算。所有标记的方格必须形成一个连续的区域, 即区域内任意两点之间都可以找到一条由相邻的方格所形成的路径。如图 2.17 所示就是 n=4 时的答案。问 n 怎样取值才能使本题有解?
现在我们来证明对于奇数个标记方格并且每一方格都有奇数个标记邻居, 是无解的。假设可能有解, 我们将得到如下矛盾关系。一方面, 如果将每一个标记方格的邻居数目相加, 将得到一个偶数, 这是因为邻居关系是相互的, 每一个邻居关系 都要计算两次。另一方面, 由于每一个方格都有奇数个邻居, 标记方格的总数是奇数, 所以邻居的总数应该是奇数。
73 逮公鸡
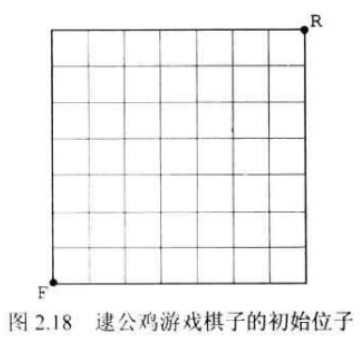
在如图 2.18 所示的棋格上进行逮公鸡游戏, 棋子 F 代表农场主在棋盘左下角; 棋子 R 代表公鸡在棋盘右上角。农场主和公对交替走棋直到公鸡被逮住。每次走棋, 农场主和公鸡都可以移动到上下左右方向上邻近的方格中, 当农场主移动到公鸡所在的格中时公鸡被逮住。
(a) 如果农场主先走, 他能逮住公鸡吗? 如果可以, 设计一个算法计算最少需要走多少步棋, 如果不可以, 解释其原因。当然, 我们假定公鸡不会主动配合农场主逮住自己。
(b) 如果农场主后走, 他能逮住公鸡吗?
我认为参考答案的思路是对的,但是结果错了,14应该改成13,其他地方都不需要改。
76 高效的车
在国际象棋里的车, 可以水平移动到它当前位置所在行的任意一格, 或者垂直移动到它当前位置所在列的任意一格。那么, 对于一个 n * n 的象棋盘来说, 车要通过所有格子所需最小的步数是多少? (注意, 并不需要开始和结束的位置在同一格中; 另外, 对于开始和结束的格子来说, 默认为是通过了的。)
78 直三格板平铺
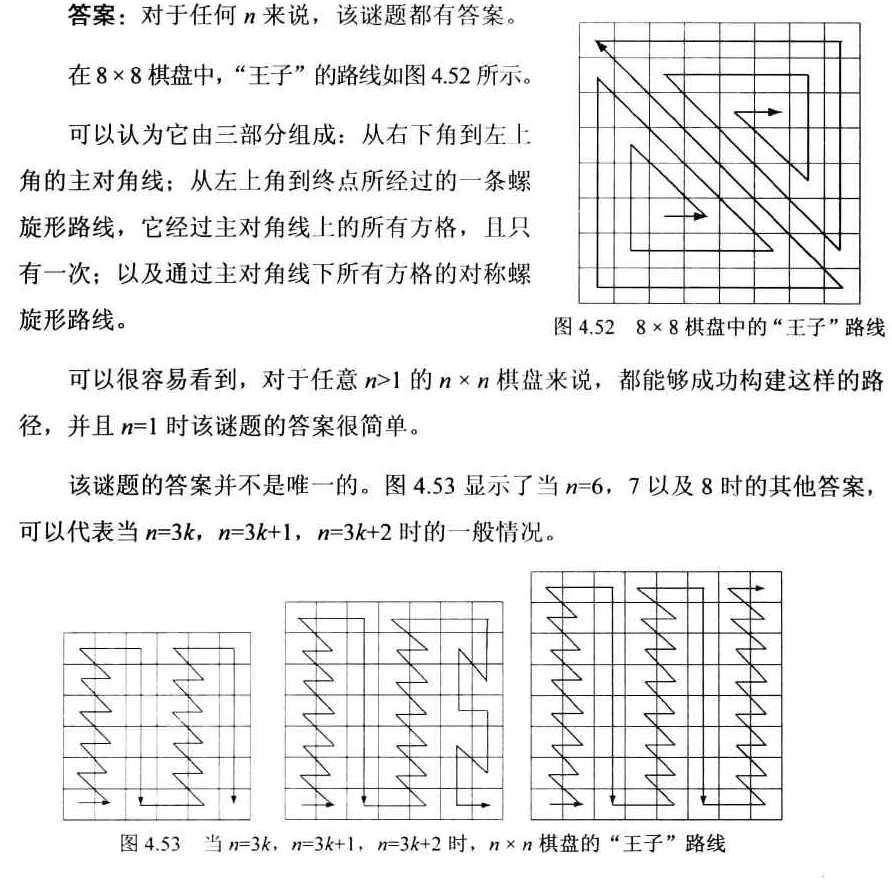
80 王子之旅
其实如果n=3k+1的情况从左上角开始,那么3种情况就几乎是一样的了。
81 再论名人问题
总结起来就是2个步骤,第1个步骤找出唯一可能是名人的人,需要n-1步,也就是每一步排除一个人
第2个步骤考虑这个人到底是不是名人,需要问其他n-1个人是否认识他,他是否认识其他n-1个人,一共需要2(n-1)-1步,减掉1是因为有一步和第1个步骤里面重复了。
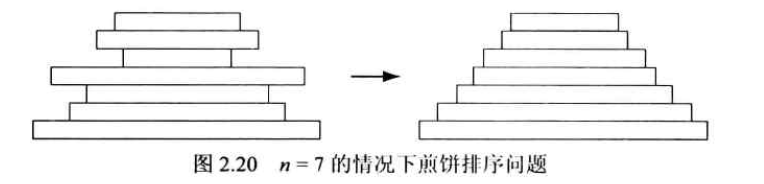
84 煎饼排序
存在 n 个大小各异的煎饼, 它们彼此重叠在一起。允许你用一个平底铲, 将其塞到其中一个煎饼下, 并把铲子上面所有的煎饼都翻转过来。我们的目标是把煎饼按大小排序, 使得最大的在最下面。图 2.20 显示在 n=7 时该问题的一个实例。请设计一个算法来解决该谜题, 并且得出该算法在最糟糕的情况下所需要的翻转次数。
答案: 当给定的煎饼个数 n>1 时, 该问题能够在 2n-3 次翻转内解决。
减而治之策略形成了下面算法的概要。重复以下步骤, 直到该问题得以解决: 通过一次翻转, 将还末处在最终位置上的最大的煎饼放到最上面, 然后用另一次翻转将它放到下面最终的位置。
在最糟糕的情况下所需要的翻转次数,就是2n-3
然而在编程之美上有个很难的问题,问,任意次序的n个烙饼翻转排序所需的最小翻转次数是多少?这个问题太难了,即使是n=14也是目前未解之谜。
85 散步谣言1
有 n 个人, 各自都知道一个不同的谣言。他们想要通过发送电子消息来与彼此 分享这些 “新闻”。要想保证每一个人都知道所有的谣言, 那么他们所需要发送的电子消息数最少是多少? 假设每一次发送, 发送者都将他或她所知道的所有谣言都发送了, 并且每个消息只能有一个接收者。
答案是2n-2,出现第一个知道所有谣言的人至少需要n-1步,唯一的方法就是接力。从出现第一个人开始,到所有人都知道所有谣言,也至少需要n-1步,唯一的方法也是接力。当然,接力的顺序不固定。
86 散步谣言2
有 n 个人, 各自都知道一个不同的谣言。他们想要通过一系列的双边对话 (比 如说, 通过电话) 来分享所有的谣言。请设计一种有效 (在通话的总数上) 的算法来解决该问题。假设每一次对话过程中, 通话双方会交换所知道的所有谣言。
上面提到的文章,第一篇是Spreading gossip efficiently,内容如下:
——————————————————————————————————————————
——————————————————————————————————————————
第2篇是Hard-to-Solve Math Puzzles by Derrick Niederman,我没找到免费阅读的地方。
87 倒置的玻璃杯
桌子上有 n 个玻璃杯, 都是倒置过来的。允许你每次翻转其中的 n-1 个玻璃杯。现在找出所有的 n 值, 使得所有的玻璃杯都能朝上, 并且描述一下能使翻转次 数最小的算法。
88 蟾蜍和青蛙
90 座位重排
生成全排列的Johnson–Trotter算法
91 水平的和垂直的多米诺骨牌
92 梯形平铺
93 击中战舰
94 搜索排好序的表
100 个不同的数字被写在 100 张卡片上, 每张卡片一个数字。卡片被排列成 10行10列, 在每一行 (从左至右) 每一列 (从上至下) 都是递增的顺序。每一张卡片都是面朝下的, 所以你看不见写在卡片上的数字是多少。现在请问你能不能设计一个算法, 使得你在翻动卡片次数小于 20 的情况下, 即可以确定一个给定的数字是否被写在其中的一张卡片上?
答案: 首先从序列右上角的卡片开始翻转, 然后将它的数字和正在搜寻的数字 进行对比。如果两个数字相等, 该问题就解决了。如果搜索的数字小于翻转卡片上 的数字, 那么, 搜索的数字不可能在最后一列, 因此可以移动到卡片左边相邻的列。 如果搜索的数字大于翻转卡片上的数字, 那么, 搜索的数字不可能处在第一行上, 因此可以移动到下面的一行。重复以上操作, 直到找到正在搜索的数字,或者搜索已经超出了边界条件, 至此, 问题就得以解决了。
该算法翻转卡片所产生的序列, 形成了一条锯齿线, 由序列的右上角向左或者向下到达某一卡片的片段构成。这样的最长曲线是在左下角结束的, 并且总共翻起了 19 张卡片。不可能存在更长的锯齿线了, 因为它不可能有超过 9 个水平的片段 和 9 个垂直的片段。
PS:
同 剑指 Offer 04. 二维数组中的查找 力扣OJ 剑指 Offer(1-30)_nameofcsdn的博客-CSDN博客
95 最大-最小称重
96 平铺楼梯区域
97 topswops游戏
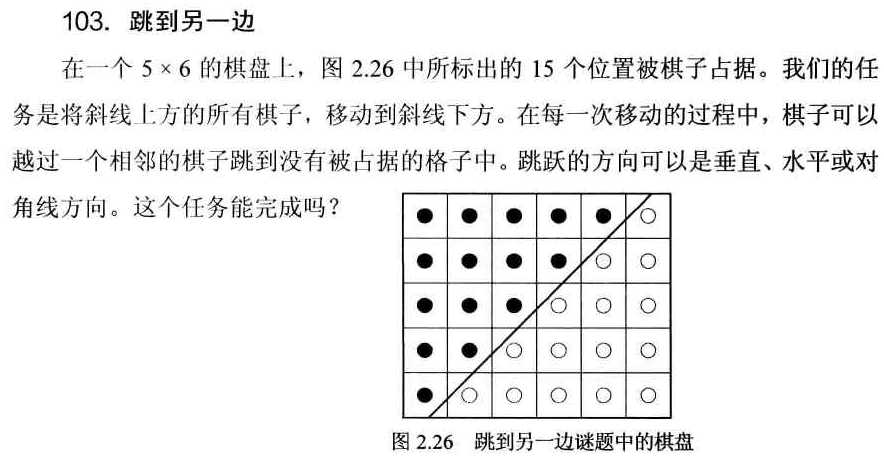
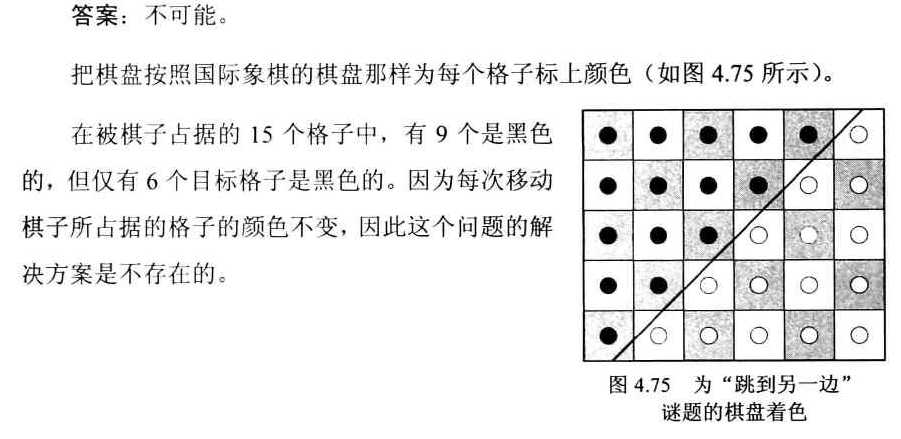
103 跳到另一边
106 开灯
107 狐狸和野兔
111 反转硬币三角形阵
112 再次讨论多米诺平铺问题
113 拿走硬币
我的思路:
一方面,T最后会变成H,会有1次翻转,H最后还是H,有0次或者2次翻转
所以所有硬币的翻转总次数为T的数量加上一个非负偶数
另外一方面,对于一开始相邻的2枚硬币(有n-1组),先被拿走的肯定会让后被拿走的硬币翻转一次
所以所有硬币的翻转总次数为n-1
所以,T的数量和n-1的奇偶性相同,即H的数量为奇数
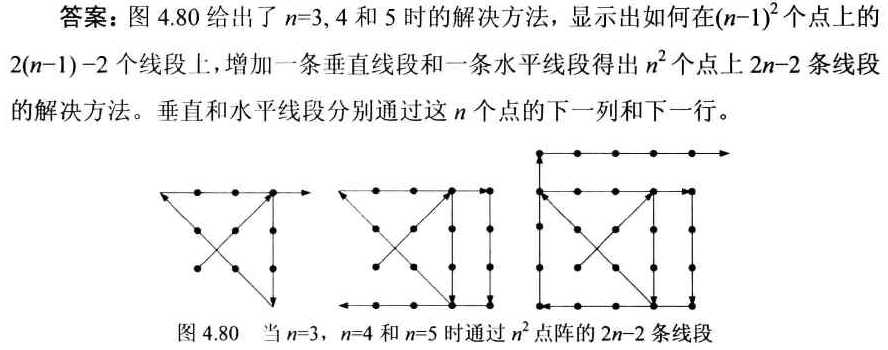
114 划线过点
当n=3的时候要用4条线一笔画完,其实就是突破想象力的9个点
115 Bachet的砝码
116 轮空计数
119 有色三格板平铺
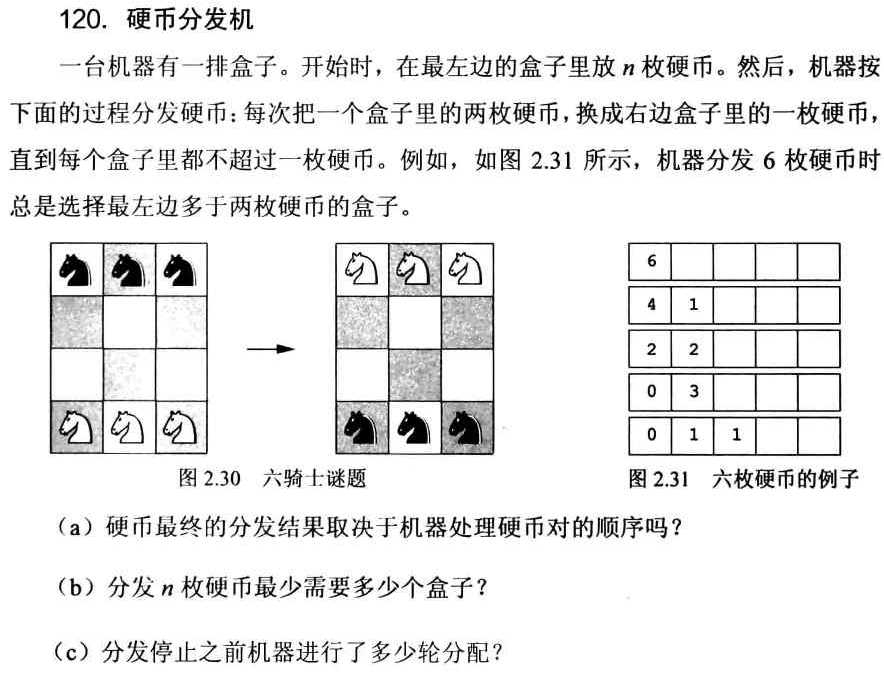
120 硬币分发机
(c)还有更简单的解法:
每次分配硬币的总数都会减少1,刚开始有n枚,最后有n的二进制中1的数量,所以分配的次数就是n减n的二进制中1的数量
121 超级蛋测试
122 议会和解
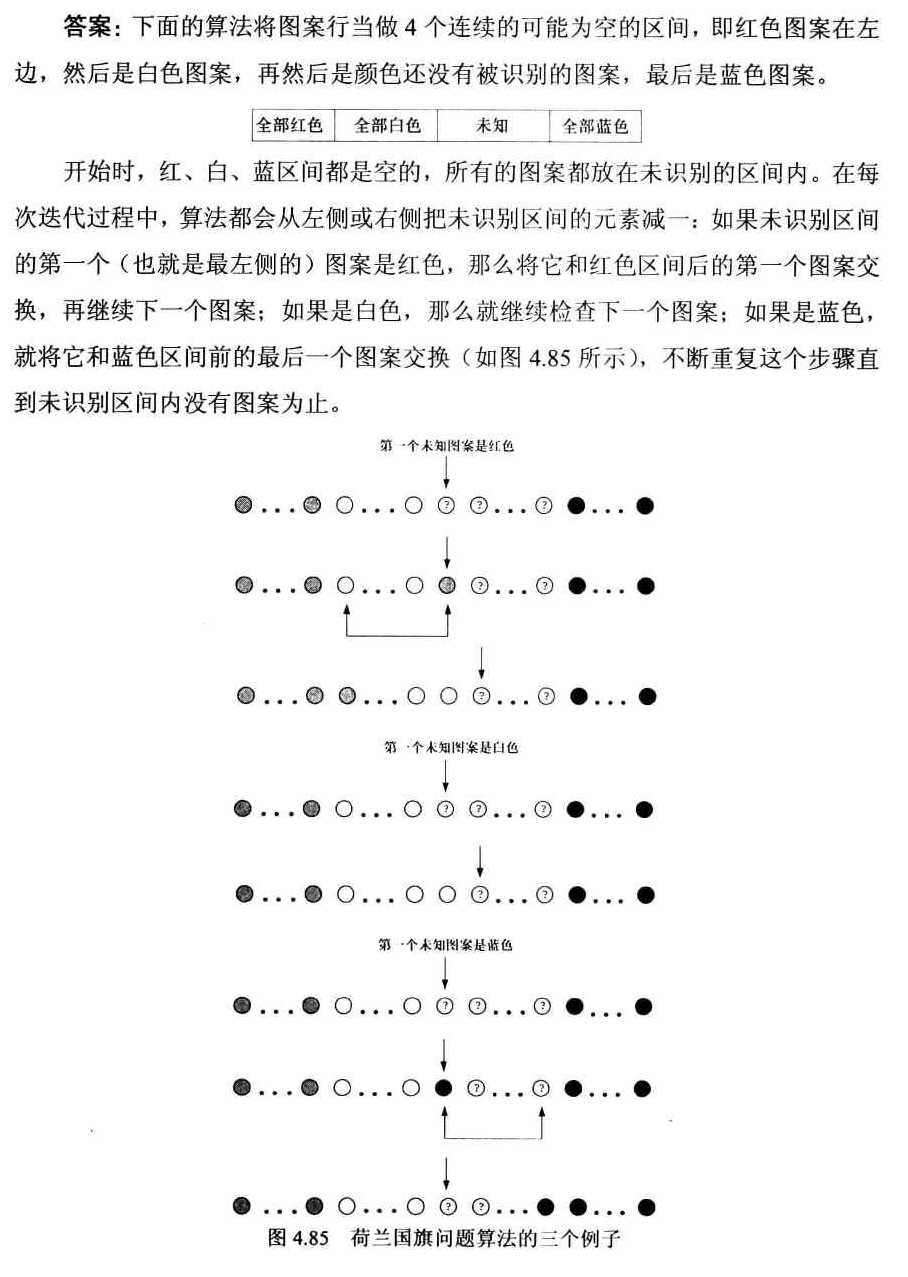
123 荷兰国旗问题
这个算法的交换步骤很少,但是并不是最少的。
例如红蓝白蓝4个方格,按照这个算法需要交换2次,实际上最少只需要1次。
124 切割链条
137 跳跃成对2
今天的文章《算法谜题》分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/68249.html