这个问题让我们从曲线的微分开始说起。
1 曲线的微分
比如,有曲线
给出
要找到一个直线段来近似这个曲线段,也就是找到这个曲线段的微分:
此微分的特点是,当
2 切线
这个微分其实就是切线。
2.1 最初印象
初学几何的时候,切线是这么定义的:
比如这就是圆、椭圆的切线:
但是这个定义推广到所有曲线上是不成立的:
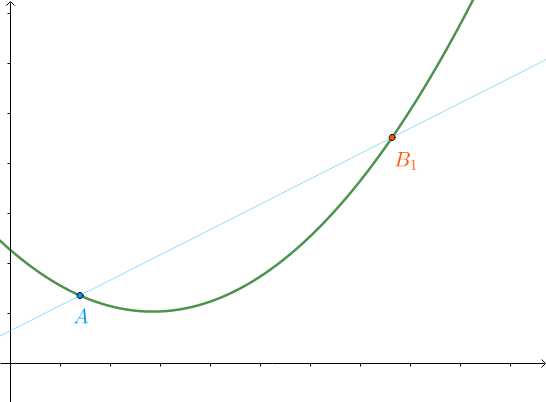
2.2 割线的极限
我们需要用极限来定义切线。比如说,要求曲线

在


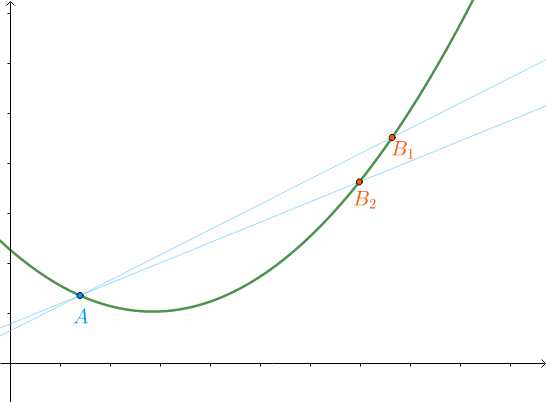
然后寻找



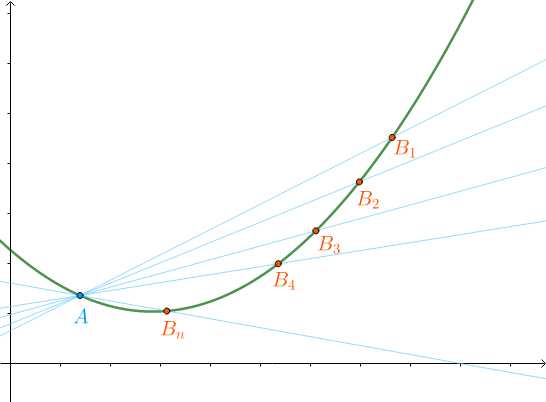
以此类推,找到点
把这些割线组成数列:
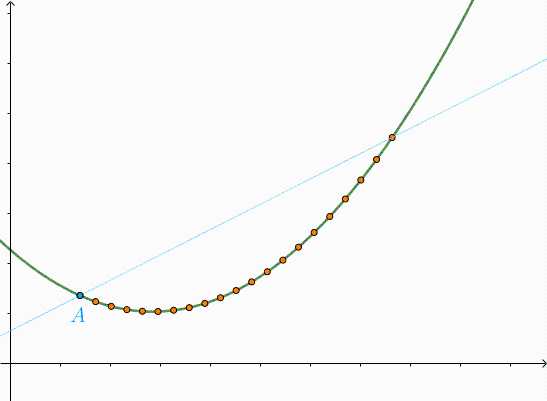
它的极限
3 导数
刚才只是给出了切线的定义,但是还是不能把切线求出来。下面来看看怎么求。
3.1 斜率
要求


其中

就可以得到切线的函数。
3.2 导数
容易有以下推论:
所以来看看割线的斜率怎么求吧。假设要求

可以看到当
先把割线的斜率

因此:
根据刚才的分析可知:
这个极限就被称为
如果,不光在



不少教科书、文档会出现如下的符号,这里也一并引入:
定义
,称之为
,导函数可以用之表示为:
有时候写作
,表明对自变量
求导。
算子,英文为“operator”,操作的意思。
算子和函数还是很接近的,只是有以下区别:
在这里,
4 切线函数与微分函数
好了,咱们有了导数,可以来求切线函数以及微分函数了。
4.1 切线函数
就切线而言,知道要经过

4.2 微分函数
虽然之前一直说切线就是微分,但是微分函数和切线函数有所不同,因为它们在不同的坐标系。让我们一步步来,把这个关键点说清楚。
首先令
然后在以
以

经过一系列操作终于得到了微分函数:
数学上把一系列操作用一个符号

微分
所以微分函数也写作:
表示把原函数







因为

因此,这就是微分的代数形式:
切线函数和微分函数的区别在于,前者在

因为微分的代数形式如上,所以导数也可以记作:
所以导数也称为“微商”,即微分与微分的商。
4.3 微分的自变量、因变量
本节一直都在说,微分是函数:
那么它的自变量是什么,因变量是什么?
微分函数在


可见,自变量是

如果不光是求
4.4 微分是线性函数
虽然两者都是直线,但因为所在坐标系不同,所以切线函数和微分函数有一个重大的区别:
这个区别说明:
根据微分是线性函数这点,我们可以很方便地运用线性代数的知识来求解法线函数。
4.5 法线函数
在切点与切线垂直的直线就是法线:
放在
即(t代表tangent,n代表normal,分别是英文的切线和法线):
根据线性代数的知识,知道两个正交向量点积为0,因此:
所以:
知道法线斜率,并且知道过

最新版本可以参看:dx,dy是什么?
今天的文章DXDY是什么币_dx和dy分别表示什么「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/68368.html