计算力学——有限元编程实现

计算力学——有限元编程实现

本项目采用C++编写，主要实现了平面结构三角形三节点单元、四节点四边形等参元和八节点四边形等参元以及相应的节点荷载和线性荷载处理方法，但未实现网格的自动划分算法。

此代码完成于2020年寒假期间，为了实现相应功能查阅了许多资料也借鉴了很多大佬的博客，
为找回自己的学习状态同时回顾一下计算力学的知识，写下此文

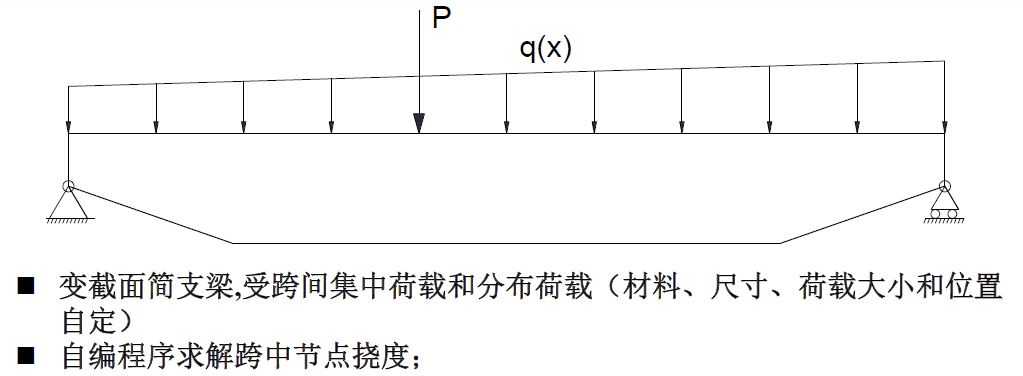
为能够更形象的表示代码实现的内容，以下述具体问题为例：

（该问题为我所学课程的大作业希望老师大大不要怪罪我）

问题分析

采用C++语句面向对象的方式实现目标功能，基于PPT所示框架引入类的思想，将单元视为基础类，创建一个供不同形状单元继承的接口类 “ShapeInterface”, 在接口类中声明不同类型单元共有的功能，即：计算单元应力阵、应变阵、刚度矩阵和总刚集成方法、总荷载集成方法。
让不同类型单元继承接口类并实现相应的功能以及单元特有功能，如：计算等参元的 ”Jacobi“ 矩阵等。
通过上述的方法即可实现：由单元自行求解 ”单元刚度和荷载“ 并自动集成到 ”总体刚度和荷载“ 的目标。
从而将问题分解为：”各类型单元各自求解方法的实现“ 和 ”主程序中对单元的初始化”。

UML图

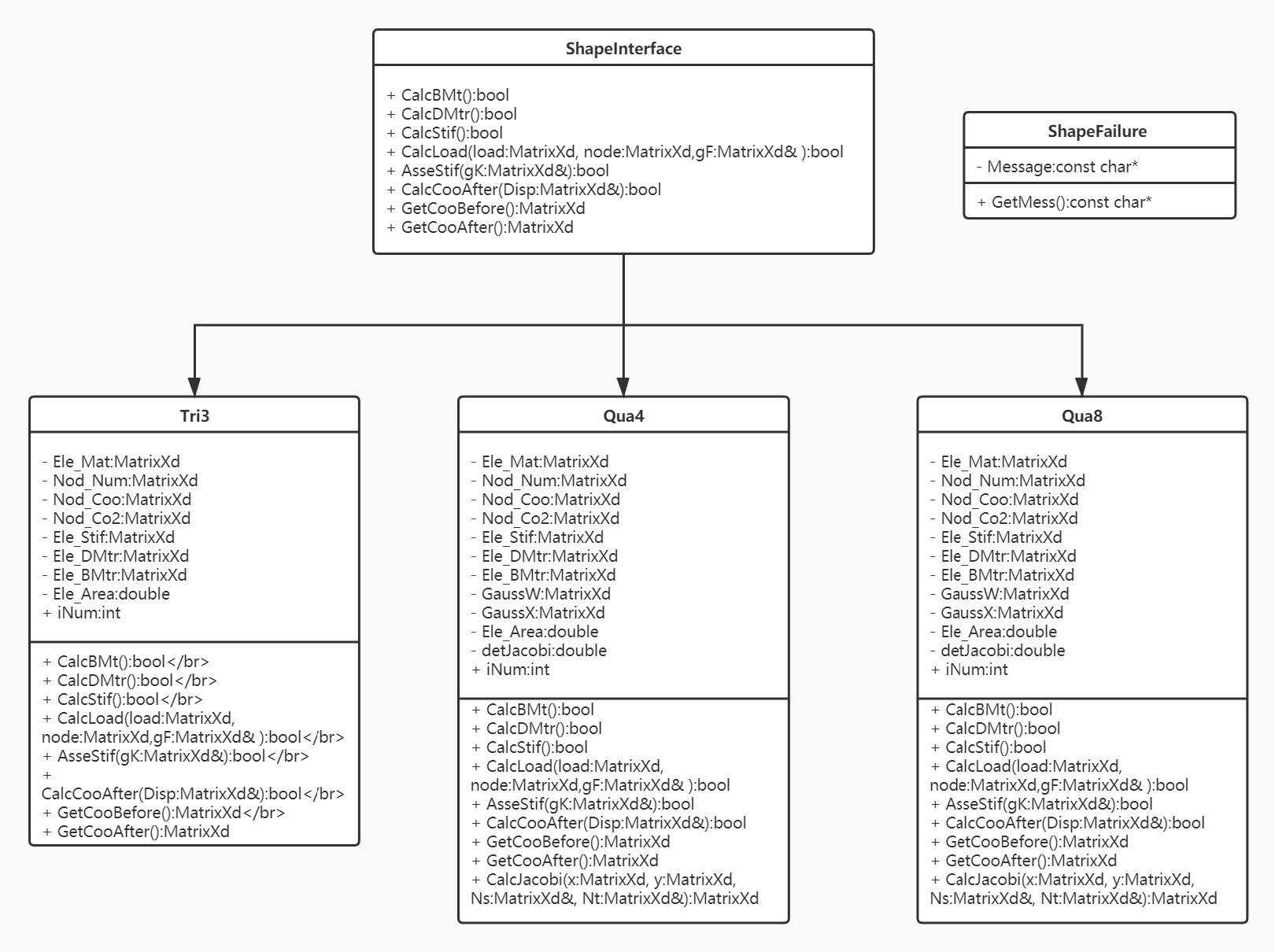
下图为接口类 “ShapeInterface”, 异常类 “ ShapeFailure”, 以及三种单元的UML类图。

Tri3 : 表示三节点三角形单元
Qua4 : 表示四节点四边形等参元
Qua8 : 表示八节点四边形等参元
（因为非计算机科班因此类图的绘制可能存在许多问题，这里贴出来的目的仅为大家更好理解整个代码的结构）

单元初始化

根据计算力学所学到的知识，单元刚度矩阵和单元节点荷载的求解分别需要如下参数：

可以看出实质上只有材料属性，节点编号以及节点坐标属于单元的固有属性，而单元的节点荷载对于不同的荷载输入会有不同的响应，因此在初始化单元时仅需要刚度矩阵 ”材料属性“, ”节点编号“, ”节点坐标“三项数据；

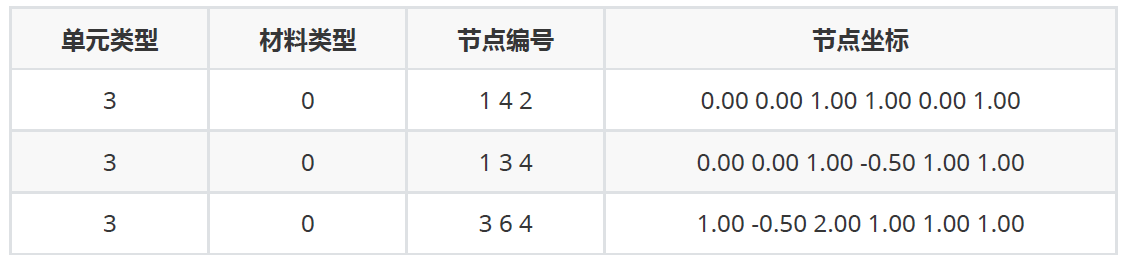
本程序采用文件读入的方式实现数据的写入，以三角形网格划分为例，其文件部分数据如下所示：

单元类的实现

以最复杂的八节点四边形等参单元为例，依次说明该类声明的各方法的实现

说明

由于我删除了写报告的Typora源文件，所以只好以留档的PDF截图介绍单元类的实现，希望能够帮助大家理解每一个方法具体实现了什么。

此外，由于自己实现矩阵运算太过麻烦且已经在数值分析课程的编程作业里编写过矩阵运算的代码因此在本项目中所有的矩阵运算均采用了开源矩阵计算工具：Eigen
对于Eigen的学习和使用可以参考 Eigen: C++开源矩阵计算工具——Eigen的简单用法

最后贴上 Shape.h 文件代码和整体工程文件（写的很烂又很长以至于贴上后太长了所以换成上传的方式）

设置应该是0积分，仅供参考使用哦！！！

[文件审核中，下次再贴上来…]

Shape.h代码

/*************************************************** * Copyright(C): 本代码所代码所有版权为gzx所有 * @brief : 主要实现了“三节点三角形”、“四节点四边形”和“八节点四边形” 单元受线性荷载和集中荷载作用下的有限元分析计算 * @autor : gzx * @version : 1.0.0.0 * @date : 2020/2/20 00:27 **************************************************/
#include <iostream>
#include <Eigen/Dense>
#pragma once
using namespace Eigen;
/** * @brief ShapeSpace命名空间用于编写不同形状单元 * 该命名空间实现了异常类、接口类以及继承接口类的不同形状单元 */
namespace ShapeSpace
{ 
   
	/** * @brief ShapeFailure-异常类 * 实现非正常输入的报错提醒 */
	class ShapeFailure 
	{ 
   
	private:
		const char* Message;
	public:
		ShapeFailure(const char* msg);
		const char* GetMess();
	};
	/** * @brief ShapeInterface-接口类 * 通过虚函数方式声明不同单元共有的方法用于形状子类的继承 */
	class ShapeInterface
	{ 
   
	public:
		bool CalcBMtr(double s, double t)throw(ShapeFailure);											///计算B矩阵
		virtual bool CalcDMtr()throw(ShapeFailure) = 0;													///计算D矩阵
		virtual bool CalcStif()throw(ShapeFailure) = 0;													///计算K矩阵
		virtual bool CalcLoad(MatrixXd load, MatrixXd node, MatrixXd& gF)throw(ShapeFailure) = 0;		///计算F矩阵
		virtual bool AsseStif(MatrixXd& gK)throw(ShapeFailure) = 0;										///集成gK
		virtual bool CalcCooAfter(MatrixXd& Disp)throw(ShapeFailure) = 0;								///计算单元变形后坐标
		virtual MatrixXd GetCooBefore()throw(ShapeFailure) = 0;											///返回受荷前单元坐标
		virtual MatrixXd GetCooAfter()throw(ShapeFailure) = 0;											///返回受荷后单元坐标
	};
	/** * @brief Tri3-三节点三角形单元 * 实现三节点三角形单元的刚度矩阵、荷载矩阵等的求解 */
	class Tri3:public ShapeInterface
	{ 
   
	private:
		MatrixXd Ele_Mat;	///单元材料属性
		MatrixXd Nod_Num;	///单元结点编号
		MatrixXd Nod_Coo;	///单元结点坐标
		MatrixXd Nod_Co2;	///变形结点坐标
		MatrixXd Ele_Stif;	///单元刚度矩阵
		MatrixXd Ele_DMtr;	///单元弹性矩阵
		MatrixXd Ele_BMtr;	///单元应变矩阵
		double Ele_Area;	///单元面积
	public:
		const int iNum = 3;
		Tri3(MatrixXd& ele_mat, MatrixXd& nod_num, MatrixXd& nod_coo);
		bool CalcBMtr()throw(ShapeFailure);
		bool CalcDMtr()throw(ShapeFailure);
		bool CalcStif()throw(ShapeFailure);
		bool CalcLoad(MatrixXd load, MatrixXd node, MatrixXd& gF)throw(ShapeFailure);
		bool AsseStif(MatrixXd& gK)throw(ShapeFailure);
		bool CalcCooAfter(MatrixXd& Disp)throw(ShapeFailure);
		MatrixXd GetCooBefore()throw(ShapeFailure);
		MatrixXd GetCooAfter()throw(ShapeFailure);
	};
	/** * @brief Qua4-四节点四边形单元 * 实现四节点四边形单元的刚度矩阵、荷载矩阵等的求解 */
	class Qua4:public ShapeInterface
	{ 
   
	private:
		MatrixXd Ele_Mat;	///单元材料属性
		MatrixXd Nod_Num;	///单元结点编号
		MatrixXd Nod_Coo;	///单元结点坐标
		MatrixXd Nod_Co2;	///变形结点坐标
		MatrixXd Ele_Stif;	///单元刚度矩阵
		MatrixXd Ele_DMtr;	///单元弹性矩阵
		MatrixXd Ele_BMtr;	///单元应变矩阵
		MatrixXd GaussW;	///Gauss加权值
		MatrixXd GaussX;	///Gauss积分点
		double Ele_Area;	///单元面积
		double detJacobi;	///J矩阵行列式
	public:
		const int iNum = 4;
		Qua4(MatrixXd& ele_mat, MatrixXd& nod_num, MatrixXd& nod_coo);
		bool CalcBMtr(double s, double t)throw(ShapeFailure);
		bool CalcDMtr()throw(ShapeFailure);
		bool CalcStif()throw(ShapeFailure);
		bool CalcLoad(MatrixXd load, MatrixXd node, MatrixXd& gF)throw(ShapeFailure);
		bool AsseStif(MatrixXd& gK)throw(ShapeFailure);
		bool CalcCooAfter(MatrixXd& Disp)throw(ShapeFailure);
		MatrixXd GetCooBefore()throw(ShapeFailure);
		MatrixXd GetCooAfter()throw(ShapeFailure);
		MatrixXd CalcJacobi(MatrixXd x, MatrixXd y, MatrixXd& Ns, MatrixXd& Nt)throw(ShapeFailure);
	};
	/** * @brief Qua8-八节点四边形单元 * 实现八节点四边形单元的刚度矩阵、荷载矩阵等的求解 */
	class Qua8 :public ShapeInterface
	{ 
   
	private:
		MatrixXd Ele_Mat;	///单元材料属性
		MatrixXd Nod_Num;	///单元结点编号
		MatrixXd Nod_Coo;	///单元结点坐标
		MatrixXd Nod_Co2;	///变形结点坐标
		MatrixXd Ele_Stif;	///单元刚度矩阵
		MatrixXd Ele_DMtr;	///单元弹性矩阵
		MatrixXd Ele_BMtr;	///单元应变矩阵
		MatrixXd GaussW;	///Gauss加权值
		MatrixXd GaussX;	///Gauss积分点
		double Ele_Area;	///单元面积
		double detJacobi;	///J矩阵行列式
	public:
		const int iNum = 8;
		Qua8(MatrixXd& ele_mat, MatrixXd& nod_num, MatrixXd& nod_coo);
		bool CalcBMtr(double s, double t)throw(ShapeFailure);
		bool CalcDMtr()throw(ShapeFailure);
		bool CalcStif()throw(ShapeFailure);
		bool CalcLoad(MatrixXd load, MatrixXd node, MatrixXd& gF)throw(ShapeFailure);
		bool AsseStif(MatrixXd& gK)throw(ShapeFailure);
		bool CalcCooAfter(MatrixXd& Disp)throw(ShapeFailure);
		MatrixXd GetCooBefore()throw(ShapeFailure);
		MatrixXd GetCooAfter()throw(ShapeFailure);
		MatrixXd CalcJacobi(MatrixXd x, MatrixXd y, MatrixXd& Ns, MatrixXd& Nt)throw(ShapeFailure);
	};
}

应该没人看到这了吧，写这么多好像暴露学校了，(lll￢ω￢)，不过这门课应该没什么人用C++写吧

今天的文章计算力学——有限元编程实现分享到此就结束了，感谢您的阅读。