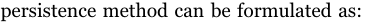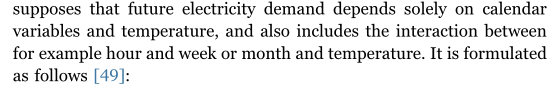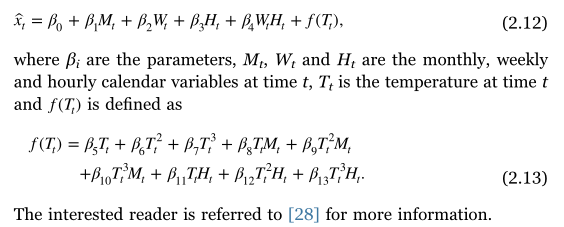前言

题目： Review on probabilistic forecasting of photovoltaic power production and
electricity consumption
期刊： renewable and sustainable energy reviews 2018
论文地址：Review on probabilistic forecasting of photovoltaic power production and
electricity consumption

  由于本篇综述实在太长，故分为三部分，此乃第一部分。

Abstract

  一方面，光伏（PV）系统在建筑环境中的渗透率越来越高，另一方面，电力消耗的随机性日益增加，例如电动汽车（EV），因而，准确预测变得更加重要和更具挑战。
  本文重点介绍了以下两个方面：

1. 太阳能概率预测（PSPF）和负荷预测（PLF）领域的最新进展。一个重要的发现是：没有一种特定的模式可以适用于任何情况！
2. 分析现有技术并评估不同方法的性能，以及这些方法在何种程度上可以推广，以便它们不仅在其设计的数据集上表现最佳，还可以在其他数据集或不同的案例研究上使用。

Keywords

  Probabilistic forecasting 概率预测
  Electricity consumption 电力消耗
  Photovoltaic 光伏
  Solar radiation 太阳辐照
  Irradiance 辐照度
  Prediction interval 预测区间

1. Introduction

  全球变暖正在加剧，为了实现碳排放量的减少，向太阳能和风能等可再生能源（RES） 转型势在必行。并且依据目前数据来看，太阳能发电在很多国家已经有了一定规模了。

  此外，研究发现随着光伏集成度的增加可能会出现一些问题，例如电压波动，馈线负载，电网损耗和增加的短路电流[10，11]。此外，经过文献综述，Ropp等人[12]得出结论，40-50％的分布式发电（DG）穿透水平可能导致由于云层变化，孤岛变化和短路电流增加引起的异常电压波动的严重问题。因此，为了减少待机的常规发电厂的数量和由于不确定性和错误预测而产生的成本，准确的光伏发电或太阳辐照度预测对于可再生能源正确地集成到发电组合中变得越来越重要。尽管该主题存在大量研究，但仍被认为相对不成熟[13]。
  总结：光伏集成度增加会导致一些问题出现，准确的光伏发电以及太阳辐照度预测很重要，但该领域现阶段不是很成熟。

  一般而言，太阳辐照度预测和光伏发电预测之间存在差异。前者的结果可以用在描述PV系统及其规格的物理模型中，而后者可以由例如公用事业直接使用以相应地规划它们的操作。由于太阳辐照度和光伏系统输出自然显示出强相关性[14]，统计预测的方法在这方面是相似的。相反，在物理预测(例如数值天气预测(NWP))的情况下，人们预测大气的状态，也需要PV系统的物理模型。
  总结：太阳辐照度预测用在PV系统的物理模型中，而光伏发电预测用于提供发电计划。

  另一方面，已知电力消耗是可以预测的，并被视为一个成熟的领域[13]，大中型公用事业在日前市场中实现 3 %或更低的预测误差[25]。然而，随着智能电网的出现，出现了新的问题，特别是与需求响应（DR）和需求侧管理（DSM）相关的问题。这些技术允许消费者基于例如在非高峰时段降低购买关税的价格激励来转移他们的电力消耗，并且因此，这给电网运营商带来了新的挑战。 Hong和Fan发现，在这种情况下，公用事业公司将需要执行一次预测和两次预测，因为需要从受价格激励影响的模式中辨别出正常的消费模式[26]。最近，动态需求响应或D2R这一术语是由Aman等人创造的，这意味着通过智能电表数据的出现，需求响应将变得更具动态性，这反过来将在住宅负荷预测方面带来额外挑战。具有高时间分辨率往往更具波动性[27]。
  总结：电力消耗的预测被认为是一个相对成熟的领域。但SG的出现带来了需求响应与需求侧的管理的问题，需求响应将变得更加具有动态性。

  传统上讲负荷预测按极短期负荷预测(VSTLF)、短期负荷预测(STLF)、中期负荷预测(MTLF)和长期负荷预测(LTLF)进行划分，预测区间分别为1天、2周、3年和30年。但是也有一些更为粗略的划分，比如只是分为短期和长期，还有的分为STLF、MTLF和LTLF，预测窗口分别为1小时到1周、1周到1年和1年以上，这个标准并不是固定的。
  但LTLF通常被认为对决策者和传输系统运营商（TSO）感兴趣，此外，由于欧盟（EU）总能耗的 40％是由建筑物造成的[32]，因此一些评论报告侧重于建筑物能耗预测[33，34，35，36]。

  这一段总结了前面提到的几篇论文具体干了些什么事情。我认为值得注意的有：

1. [26]中讨论了17篇负荷预测文章，之后他们将重点放在了他们认为以前没有做过的概率负荷预测(PLF) 上，说明PLF涉及的人还不是很多。
2. [23]以及[36]发现了一个趋势，尽管人工神经网络(ann)仍然是目前使用最多的对辐照度和负荷进行预测的模型，但梯度增加，随机森林和支持向量机在科学界得到越来越多的关注。
3. [22]评估并比较了三种不同类型的ann在预测中国日全球辐照量方面的性能。他们发现，精度强烈地依赖于模型和位置，有时产生显著不同的结果，但总体多层感知器(MLP)和径向基神经网络(RBNN)优于其余的神经网络和物理模型。

  这里多次提到了 ‘‘net demand’’ 一词，即净需求。在城市和住宅区净需求预测变得很难，一方面是因为光伏系统的细节，比如倾斜和方位角等。另一方面的原因是人们的各种行为是随机的，比如用电习惯等等之类的。
  本文分别回顾了在不同时间范围内对太阳能（PSPF）和负荷（PLF）进行概率预测的最新进展，以描绘出将PSPF和PLF结合用于净需求预测的机会。本文首先是概述了最先进的太阳辐照度和光伏功率预测，然后概述了最先进的负荷预测，特别关注城市和居民用电。这两种情况下重点都放在概率预测。因为与预测性预测相比，它传达了更多有关未来发电和消费的信息。


因此，说了这么久，本文的目的终于浮出水面：

1. 提供PSPF和PLF的性能指标，方法和最新进展的广泛概述。
2. 发现研究差距。
3. 找到PSPF和PLF之间的共同点，为净需求预测开辟道路。
4. 评估了对上述性能指标进行标准化的必要性。

本段说明了接下来几部分的内容，可以总结如下：

1. 第二部分介绍了确定性预测和概率性预测的一些基本定义、模型以及性能指标。概率预测的均值可以被解释为确定性预测。
2. 第三部分概述了当前比较常见的用于PSPF和PLF的预测技术，并且着重讨论了非参数统计技术。因为参数化方法倾向于将确定性预测修饰成概率预测， 而确定性模型超出了本文的讨论范围。此外，非参数统计方法可用于直接预测，也可从确定性物理模型(如NWP)中创建概率预测。
3. 第四部分在使用的方法、预测范围和空间和时间分辨率等方面对PSPF和PLF进行了比较。
4. 第五部分是总结。

2. Basic definitions and comparison models

  本节介绍有关空间和时间范围以及分辨率的基本定义，阐述确定性和概率性预测之间的差异，并概述确定性和概率性预测的比较模型和性能指标。

2.1. Spatial and temporal horizon and resolution

2.1节讲述空间时间范围以及分辨率。

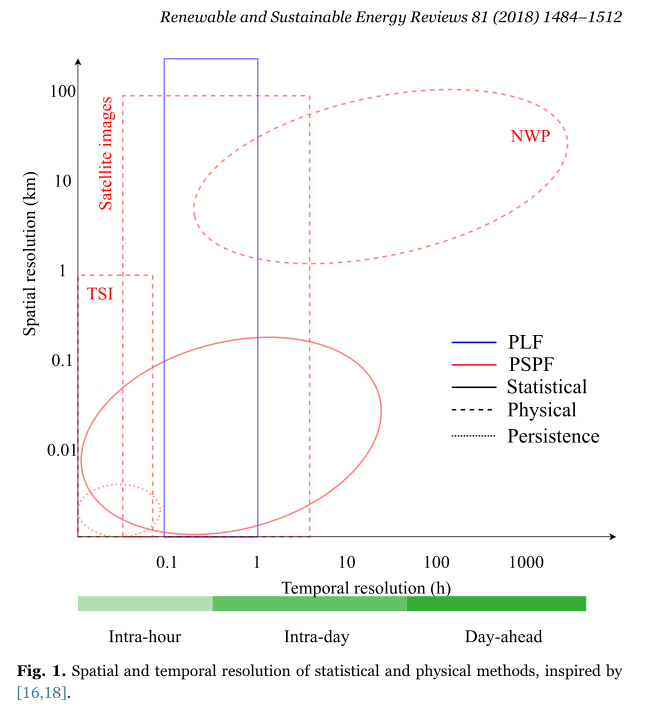
  任何预测的准确性都受到空间和时间范围和分辨率的极大影响,这里面涉及到四个参数：空间范围、空间分辨率、时间范围以及时间分辨率。 图 1 说明了统计和物理方法的空间和时间分辨率，如下所示：

  横轴为时间分辨率，纵轴为空间分辨率，蓝色代表负荷预测，红色为太阳能预测；实线为统计方法，虚线为物理方法。观察发现，红色相比蓝色充满更多变化，也就是说太阳能预测 （SPF）的方法存在比负荷预测更多的变化。同时负荷预测很少使用物理方法，but这并不意味着不考虑诸如温度的物理变量，因为这些变量对电力消耗具有显着影响。

  其次，尽管 SPF（太阳能预测）存在几种物理方法，但很少有j将它们用于概率SPF（PSPF） ，但依然存在。比如NWP（数值天气预测）预测以某些初始和边界条件运行。为了创建PSPF，可以调整这些条件并根据后续预测构建概率密度函数（PDF） 。由于NWP模型的计算要求很高，因此这是一个耗时的过程。

  第三，我们都知道，负荷预测一般通过时间序列或人工神经网络实现，比如RNN以及LSTM之类的，观察上图那个蓝色的方框可以发现，负荷预测这些方法可以在更广泛的空间分辨率上使用， 这取决于聚合的级别。其原因在于聚合水平上的电力消耗比太阳辐照度变化小，并且具有较强的重复特性，其随机性较小，因此可以避免复杂的物理建模。
  总结：这句话怎么理解？电力消耗在空间分布上的变化比太阳辐照度要小一些，因而建模更加容易。

  第四，由于NWP模型的复杂性和缺乏计算能力，空间和时间的分辨率都很粗糙，因此用于具有更大时间范围的预测。

  最后，关于短期太阳能预测范围和负荷预测的定义之间存在差异。短期SPF的范围通常是日内和日前，而STLF的范围是一天到两周。本评论将重点关注短期PSPF和短期PLF，如第1部分所述。第3部分将详细介绍图1所示的预测方法。

2.2. Deterministic forecast vs. probabilistic forecast

2.2节讲述确定性预测和概率预测。

  总的来说，以前的研究主要集中在确定性预测或者点预测上。Hong和Fan指出一个可能的原因是概率预测的评估与用于评估确定性预测的绩效指标相同，但是前者表现差于确定性预测，所以主要研究了确定性预测。从2.5节 （其中介绍了最常见的性能衡量指标） 可以得出结论，使用为点预测制定的指标评估概率预测可能会导致无效的结论。
  总结：概率预测和确定性预测的绩效指标相同，而概率预测表现较差，所以主要研究了确定性预测。

  提供具有PDF（概率密度函数）或预测区间的实用程序，即预测随机变量以特定概率测量的未来生产和需求的间隔可以说比单个值更有价值，因为它允许风险管理。应当注意，预测区间和置信区间不相同。
  重点来了：要在概率预测中构建PDF，通常有两种方法。首先，可以假设密度函数，这是参数方法。其次是非参数方法，其中没有做出这样的假设。然而，假设分布很少代表观察结果并且通常是无效的，或者至少是次优的，这说明参数方法存在一定局限性。因此，综述的大多数论文都考虑非参数方法。


  最后，关于PSPF和PLF的成熟度。洪等人[13]对此进行了图解，并得出结论认为PSPF仍然不成熟，而PLF最近在科学界已经成熟。

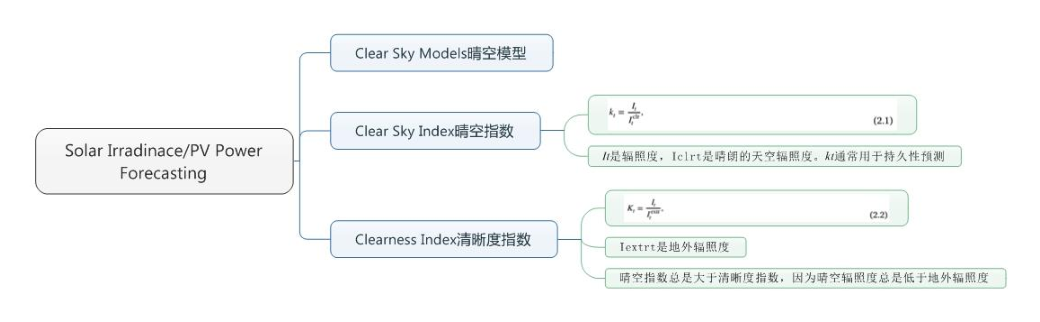
2.3. Clear sky models, and clear sky and clearness indices

2.3节讲述晴空模型，晴空指数和清晰度指数。

  晴空模型旨在模拟晴天条件下的直接法向辐照度（DNI）和漫反射水平辐照度（DHI） ，同时考虑太阳的几何形状和气象输入，如水汽含量。

  晴天辐照度通常用于标准化太阳辐照度， 以便对时间序列进行固定。 通过晴空模型或地外辐照度建模的晴空辐照度实现归一化。前者的结果称为晴空指数，其表述如下：
$$k_t=\frac{I_t}{I_t^{clr}}$$
其中$I_t$是辐照度，$I_t^{clr}$是晴空辐照度，辐照度/晴空辐照度，即晴空辐照度归一化，$k_t$称为晴空指数，用于持久性预测。

  地外辐照度归一化定义为清晰度指数$K_t$：
$$K_t=\frac{I_t}{I_t^{extr}}$$
其中$I_t^{extr}$是地外辐照度. 当然，由于没有大气层，地外辐照度比晴朗的天空辐照度更容易建模。
  Inman等人提到的一种简单的地外辐照度模型表述为：
$$I_t^{extr}=I_{0}cos({\theta }_t)$$
其中太阳常数$I_0$=1360W/m2，${\theta }_t$是时间t处的太阳天顶角。
  最后，值得注意的是，晴空指数$k_t$总是大于清晰度指数$K_t$，因为晴空辐照度总是低于地外辐照度。也就是公式1的分母是小于公式2的分母的，而它们分子相同。
  总结如下：

2.4. Benchmark methods

2.4节讲述基准方法。

  一个典型的基准方法是概率预测的非参情况，确定性预测的基准方法通常是持久性模型。

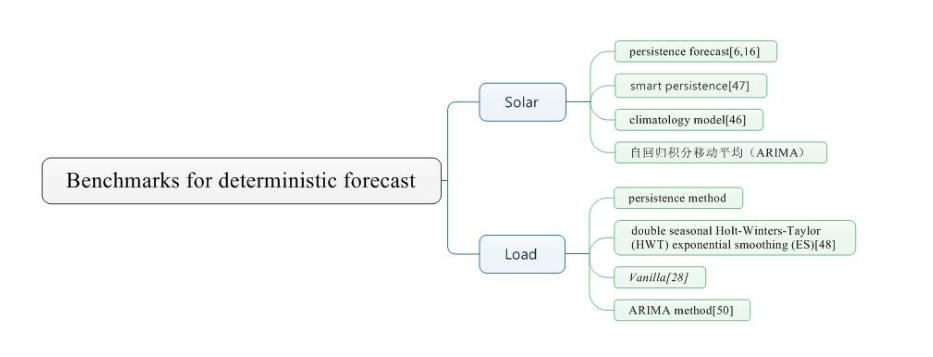
2.4.1. Benchmarks for deterministic forecast

  本节讲述确定性模型的基准，也就是上面说的持久性模型。首先是太阳能预测：


  持久性预测又称为朴素预测器。假设时间t的条件将持续到时间段t+h，这种方法在几秒甚至几分钟预测范围内非常有效，但当预测范围增加到一小时甚至超过一小时，其效果会大大降低。此外，预测技能得分公式S用来衡量所提出的模型与持久性方法相比的相对的改进。 S为0，意味着没有改进，即不确定性与可变性一样大，这是持久性预测中的情况。S大于零，则可以认为是有效的，而S≤0意味着应该拒绝所提出的模型，因为不确定性大于可变性。
  持久化方法可以表述为：

这里是${\tilde{x}}_{t+h}$预测值，$x_t$是感兴趣的时间序列在t+1时刻的测量值，例如晴空指数。

  虽然持久性是最常见的基准方法， 但最近又提出了另一种类似的方法， 称为智能持久性。不是让预测范围h的预测值$x_{t+h}$完全取决于当前观察值，智能持久性将先前h观察的平均值考虑在内。这可以表述为:
$${\tilde{x}}_{t+h}=mean[x_t,\dots ,x_{t-h}]$$

  还有一种气象学采用的基准—–气候学模型。与持久性模型及其在较短的提前期（即预测范围）中的应用相比，气候学模型通常难以在较长的预测范围内表现出色，因为它考虑了所有测量的平均值。它的形式如下：
$${\tilde{x}}_{t+h}=mean(x_t)$$

有两点需要注意：

1. 尽管气候学模型可以应用于点预测，但这种情况并不常见。然而，它在概率预测中经常作为基准模型使用， 因为有可能根据过去观测的分布构建无模型分布，我们将在下一节中展示。
2. 其它完善的方法，如自回归积分移动平均（ARIMA）有时也被用作基准，这将在下一节中更详细地解释。

接下来是负荷预测。

  关于负荷预测，没有单一的普遍基准，而是存在各种各样的基准。 本段介绍了本文所述论文中使用的几个基准，其中最简单的一个是持久性方法，即与 SPF一样的朴素预测器。

  另外一种常用的基准我们称之为：双季节性Holt-Winters-Taylor（HWT）指数平滑（ES），该方法的优点在于它能够结合两种季节性模式，例如，日内和周内循环。它的数学公式如下：

其中$\alpha ，\gamma ，\delta 和\omega$是平滑参数，${\tilde{x}}_t(k)$是预测范围k的预测。此外，季节性指数$s_1$和$s_2$确定调查中的季节周期，例如，对于上述日内和周内周期，$s_1=24$和$s_2=68$。


  Vanilla是Hong[28]在2010年提出的一种基准方法，它将新近效应考虑在内，这是心理学中的一个术语，暗示人们往往会记住他们最近读到的最好的东西。这意味着当进一步观察时，当前负荷需求对过去温度测量的依赖性降低。对此的适当数学表示是温度的移动平均值（MA）。Vanilla基准假设未来的电力需求仅取决于日历变量和温度，还包括例如小时，周或月与温度之间的相互作用。它的表述如下[49]：

其中${\beta }_i$是参数，$M_t，W_t，H_t$是时刻t的月、周、小时的日历变量，$T_t$是时刻t的温度，$f(T_t)$定义为：
$$\begin{gathered} f(T_t)={\beta }_5{T}_t+{\beta }_6{T}^2+{\beta }_7{T}^3+{\beta }_8{T}_t{M}_t+{\beta }_9{T}_t^2{M}_t \\ +{\beta }_{10}{T}_t^3{M}_t+{\beta }_{11}{T}_t{H}_t+{\beta }_{12}{T}_t^2{H}_t+{\beta }_{13}{T}_t^3{H}_t \end{gathered}$$

  ARIMA方法通常也可以用作基准，它的一个重要条件是所研究的时间序列是平稳的， 即具有恒定的均值和方差，并且存在几种方法来固定、时间序列，例如差分、变换到对数标度或标准化。ARIMA（p，d，q）模型可以多项式形式表示为[51]：

p和q表示自回归AR和MA过程的阶，ϕ(b)和θ(b)是AR和MA的参数，d表示第d个差分，b以多项式形式编写ARIMA过程所需的后向移位运算符，定义如下：
$$x_t-x_{t-1}=(1-b)x_t，此为一阶差分$$
总结如下：

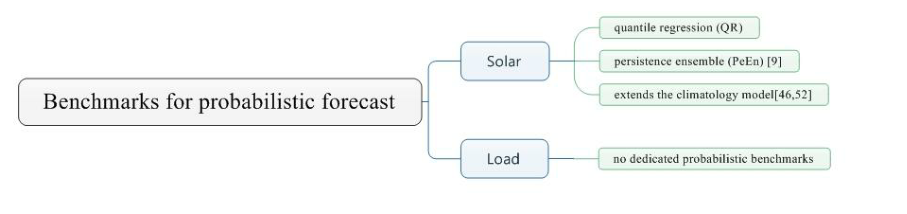
2.4.2. Benchmarks for probabilistic forecast

2.4.2节讲述概率预测的基准。

  到目前为止，没有普遍的基准方法用于比较新提出的方法的性能。例如，与SPF组合的持久性方法的情况。但是，已经提出了几个基准，这些基准在本节中提出。

  先是太阳能。除了使用分位数回归（QR）等成熟方法作为基准之外，最近还提出了另外两种方法。Alessandrini 等人提出了持久性集成（PeEn）[9]并通过查看一天中同一时间的一定量的最近测量值来生成PDF，随后可以将其排序为分位数间隔。这可以表示为 ：
$$PDF[{\tilde{x}}_{t+h}]=PDF(x_t,x_{t-1},\dots ,x_{t-m})$$

  第二种方法将气候学模型扩展到概率模型，利用过去的测量来构建PDF[46]。然而，已经进行了修改以提高准确性，例如Zamo等人[52]，他按月下令测量，以获得真实的预测。

  接下来是负荷预测。据作者了解，目前没有专门用于负荷预测的概率基准。而是用确定性基准创建概率基准。例如，Arora和Taylor（[53]）使用蒙特卡罗（MC）模拟方法生成双季节 HWT ES方法的概率预测。此外，刘等人 [49]利用姐妹模型，即具有不同滞后温度和滞后日移动平均值的模型，来构建密度分布预测。最后，Quan等人[54]利用ARIMA模型的直接一步法，以构建90％的预测区间。
  总结如下：

2.5. Performance metrics

2.5讲述性能度量。

  任何预测都应该进行准确性评估， 通常是对比朴素方法和现有方法，以便可以比较性能。由于精确度测量可用于太阳能和负荷预测，因此在这方面没有区别。关于点预测的准确度测量的综合概述可以在[6]，[55]，[56]中找到，而[57]，[58]提供了关于概率预测的上述测量的全面概述。应该指出的是，虽然本文侧重于概率预测，但点预测措施仍可应用于例如概率预测的平均值，并提供有价值的信息，特别是在短期预测的情况下[26]。

2.5.1. Deterministic forecasting

2.5.1讲述确定性预测的性能评估。

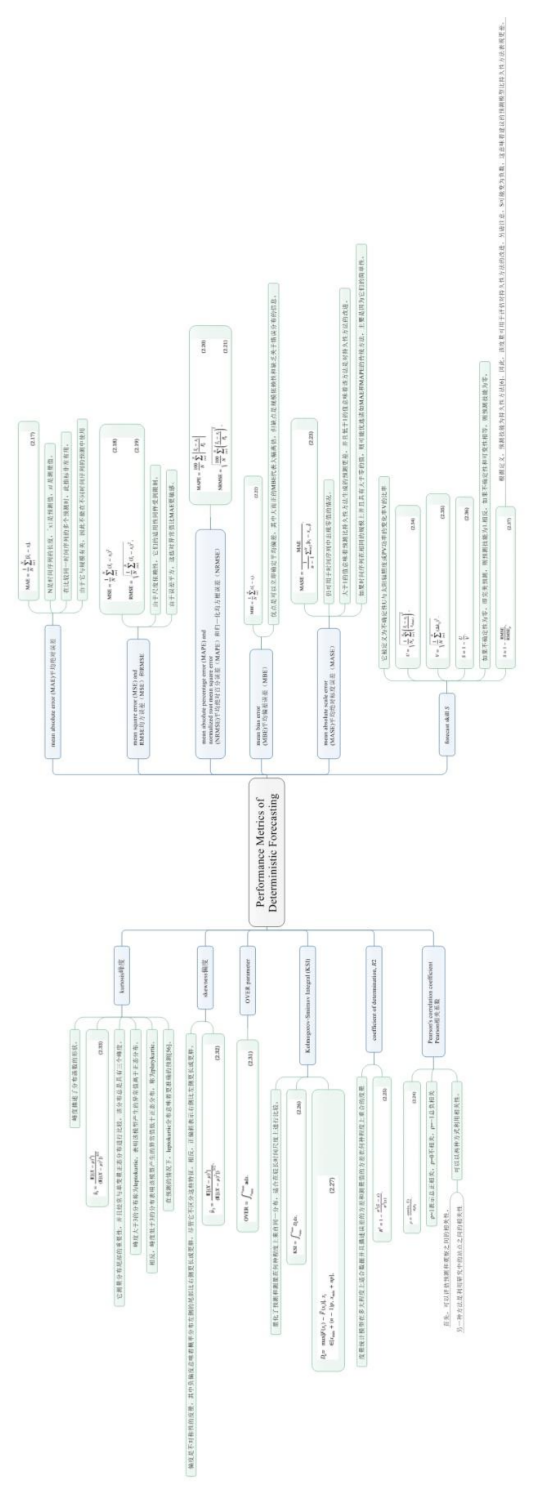
  霍夫等人[59]认为为了描述模型的性能，应该应用几个性能指标以便人们可以评估其准确性。例如均方根误差（RMSE） ，由于误差的平方，它比其他方法更严重地惩罚异常值。以下是性能指标的总和及其各自的优缺点。

  平均绝对误差（MAE）通过计算这两者之间的平均误差来显示预测的准确性，可以表述如下：
$$MAE=\frac{1}{N}\sum _{i=1}^N|{\tilde{x}}_i-x_i|$$
  N是时间序列的长度，${\tilde{x}}_i$是预测值，$x_i$是测量值。在比较同一时间序列的多个预测时，此指标非常有用。但由于它与规模有关，因此不能在不同时间序列的预测中使用，因为它具有固有的规模差异。

  均方误差（MSE）和RMSE定义为：
$$\begin{gathered} MSE=\frac{1}{N}\sum _{i=1}^N({\tilde{x}}_i-x_i{)}^2 \\ RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N({\tilde{x}}_i-x_i{)}^2} \end{gathered}$$
参数意义同MAE。由于尺度依赖性，它们的适用性同样受到限制。此外，由于误差平方，这些对异常值比 MAE更敏感。然而，因为它们分别提供了对误差的方差和标准偏差的快速认知，这些指标因其在统计建模中的理论相关性而被广泛使用[55]。


  前面也提到了，平均绝对误差（MAE）、均方误差（MSE）以及均方根误差（RMSE）不能用于比较不同时间序列之间的预测结果。为了能够比较不同时间和空间尺度上的预测，可以使用百分比误差测量。Hoff 等人[59]研究发现，对于太阳能预测（SPF），有几个分母可用于归一化误差。他们发现三个是最合适的，即平均或加权平均辐照度或已产生的功率以及光伏电站的容量。由容量标准化的平均绝对百分误差（MAPE）和归一化均方根误差（NRMSE）表述如下：
$$\begin{gathered} MAPE=\frac{100}{N}\sum _{i=1}^N|\frac{{\tilde{x}}_i-x_i}{P_0}| \\ NRMSE=\sqrt{\frac{100}{N}\sum _{i=1}^N(\frac{{\tilde{x}}_i-x_i}{P_0}{)}^2} \end{gathered}$$

这里$P_0$是SPF情况下光伏电站的额定功率。MAPE测量的优点在于它是直接且广泛接受的，例如在风力涡轮机行业[59]。与RMSE类似，NRMSE对异常值也比MAPE更敏感。 有时候，式(2.20)(2.21)用测量值归一化，即把$P_0$换成$x_i$，其缺点是假定具有含义的绝对零值，例如在温度和开尔文尺度的情况下。

  为了评估预测的偏差，即模型是否过高或过低估计，应该利用平均偏差误差（MBE），其表达式如下：
$$MBE=\frac{1}{N}\sum _{i=1}^N({\tilde{x}}_i-x_i)$$

  最近，Hyndman和Koehler[55]提出了一种新的度量，旨在独立于规模，对异常值的敏感性低于基于相对误差的相对测量和度量的方法。在平均绝对标度误差（MASE）中，使用基准方法的样本内MAE（即持久性方法）来缩放误差。MASE的表述如下：
$$MASE=\frac{MAE}{\frac{1}{n-1}{\sum }_{i=2}^N|x_i-x_{i-1}|}$$

  据作者所说，这一措施是广泛适用的，并且仍可用于时间序列中出现零值的情况。大于1的值意味着预测比持久性方法生成的预测更差， 并且低于1的值意味着该方法是对持久性方法的改进。然而，应该注意的是，作者指出，如果时间序列在相同的规模上并且具有大于零的值，则可能优选诸如MAE和MAPE的传统方法，主要是因为它们的简单性。


  两个变量之间的线性相关性，即测量值$x$和预测值㼿$\tilde{x}$，可以通过 Pearson相关系数确定，并定义如下：
$$\rho =\frac{cov(x,\tilde{x})}{{\sigma }_x{\sigma }_{\tilde{x}}}$$
这里，ρ=1表示总正相关，ρ=0不相关，ρ=−1总负相关。由于协方差cov表示两个变量一起变化多少，因此可以以类似的方式解释相关系数。例如，系数1意味着两个变量具有相同的趋势。

  确定系数$R^2$是度量统计模型在多大程度上适合数据并且描述误差的方差和测量值的方差在何种程度上重合的度量。$R^2$可以定义如下：
$$R^2=1-\frac{{\sigma }^2(\tilde{x}-x)}{{\sigma }^2(x)}$$

  Kolmogorov-Smirnov 积分（KSI）量化了预测和测量在何种程度上来自同一分布，适合在较长时间尺度上进行比较。这是一个非参数测试，其公式如下：

$$KSI={\int }_{x_{min}}^{x_{max}}{D}_{n}dx$$
其中$D_n$是每个时间间隔的累积分布函数之间的差异，定义如下：

$$\begin{gathered} D_n=max|F(x_i)-\tilde{F}(x_i)|,x_i \\ \in [x_{min}+(n-1)p,x_{min}+np] \end{gathered}$$
其中，F和$\tilde{F}$分别表示预测和测量的累积分布[61]。此外，p是间隔距离，并表示为：
$$p=\frac{x_{max}-x_{min}}{m}$$

  这里m是离散化水平，根据Espinar等人的说法 [61]选择为100，因为更高的m不会增加精度，反而带来计算时间的代价。为了确定零假设，即预测值和测量值是否具有相同的分布，可以以99%置信水平接受，Dn应低于阈值 Vc，其公式如下：
$$V_c=\frac{1.63}{\sqrt{N}},N>=35$$
其中N是时间序列的长度[61]。从式（2.26）可以看出，人们可以在整个测量范围内评估预测的累积分布与测量值的偏差，其中 KSI 值为零意味着两个分布相等。KSI测试相对于Kolmogorov-Smirnov（KS）测试的优势在于，除了总结是否拒绝或接受上述零假设外，还可以量化误差[61]。

  与KSI参数类似，OVER参数基于KS测试。但是，仅当F和$\tilde{F}$之间的差值（即 Dn）超过Vc时才计算OVER参数。为了做到这一点，需要构造一个向量a，其中包含Dn和Vc之间的差异，如果Dn大于Vc，或者在Dn小于Vc的情况下为零，其公式如下[61]：
$$\begin{gathered} a=D_n-V_c,if{D}_n>V_c \\ a=0,if{D}_n<=V_c \end{gathered}$$
进一步，OVER参数可定义为：
$$OVER={\int }_{x_{min}}^{x_{max}}adx$$


  KSI和OVER参数都可以通过临界区域$a_c$进行归一化，定义为$a_c=Vc(x_{max}-x_{min})$，这允许比较来自不同测试的上述参数[61]。将这些参数包括在预测模型的分析中是有价值的，因为与RMSE和MBE相比，可以比较预测和测量值的分布[61]。

  尽管RMSE和MAE等传统测量方法由于易于解释而具有很大价值， 但如果预测误差具有相同的均值和方差但分布不同，不允许在数据集之间进行比较。显然，重要的是要知道在单位调度的情况下模型是否始终低估或高估预测，这是由于传统热发电机的减速和加速时间相对较慢。为了获得有关分布的其他信息，可以计算预测误差的偏度和峰度。偏度是不对称性的度量，其中负偏度意味着概率分布左侧的尾部比右侧更长或更胖，尽管它不区分这些特征。相反，正偏斜表示右侧比左侧更长或更胖。偏度是第三个标准化时刻，可以定义如下[62]：
$${\tilde{\mu }}_3=\frac{E[(X-\mu {)}^3]}{(E[(X-\mu {)}^2]{)}^{\frac{3}{2}}}$$
其中X是随机变量，$\mu$是平均值。

  与偏度相似，峰度描述了分布函数的形状。具体而言，它测量分布尾部的重要性，并且经常与单变量正态分布进行比较，该分布总是具有三个峰度。 峰度大于3的分布称为leptokurtic，表明该模型产生的异常值高于正态分布。相反，峰度低于3的分布表明该模型产生的异常值低于正态分布， 称为platykurtic。在预测的情况下，leptokurtic分布意味着更准确的预测[56]。
  峰度是第四个标准化时刻，定义为[43]：
$${\tilde{\mu }}_4=\frac{E[(X-\mu {)}^4]}{(E[(X-\mu {)}^2]{)}^{\frac{4}{2}}}$$
其他指标必须与偏度和峰度结合使用，因为这些措施本身并未提供有关预测误差的足够信息。

  在预测光伏发电输出的太阳辐照度时，通常的做法是将所提出的模型与持久性方法进行比较。为了评估所提出的预测模型相对于持久性方法的改进，可以计算预测技能S。它被定义为不确定性U与太阳辐照度或PV功率的变化率V的比率。不确定性U的表述如下[6]：

$$U=\sqrt{\frac{1}{N_w}\sum _{i=1}^{N_w}(\frac{{\tilde{x}}_i-x_i}{x_{clear,i}}{)}^2}$$
其中$N_w$是子集时间窗，$x_{clear,i}$是预期的晴空辐照度。与式(2.19)相比，可以看出这些公式之间的相似性。实际上如前所述，RMSE可以看作是误差的标准差，这与预测的不确定性密切相关[6]。

  由Coimbra和Kleissl[6]定义的太阳可变性为晴空指数的阶跃变化的标准差，因此与昼夜变率无关。可变性 V 的表述如下：
$$V=\sqrt{\frac{1}{N}\sum _{i=1}^N(\Delta k_{t_i}{)}^2}$$
  随后，预测技能S可以定义如下：

$$S=1-\frac{U}{V}$$
  从式（2.36）可以看出，如果不确定性为零，即完美预测，则预测技能为1。相反，如果不确定性和可变性相等，则预测技能为零，根据定义，预测技能为持久性方法[6]。因此，该度量可用于评估对持久性方法的改进。另请注意，S可能变为负数，这意味着建议的预测模型比持久性方法表现更差。最后，Coimbra&&Kleissl[6]指出S可以通过以下公式近似：
$$S\approx 1-\frac{RMSE}{RMS{E}_p}$$
其中RMSE_{p}是持久化方法实现的RMSE。 显然式（2.37）比式（2.36）更容易计算。但如果研究人员计算了RMSE和RMSEp，它也可以追溯用于比较不同模型的结果。
  以上关于确定性预测的评估指标可以总结如下：

2.5.2. Probabilistic forecasting

2.5.2讲解概率预测的性能指标。

  尽管已经制定了专门的措施， 但前一部分的措施可以用于短期预测[26]。 然而，Hong和Fan[26]发现，概率预测处于相对不成熟阶段的主要原因之一是由于很少有完善的评估方法。应该注意的是，他们专门针对 PLF做了这个评论，但这也适用于概率辐照度预测（PIF） 。

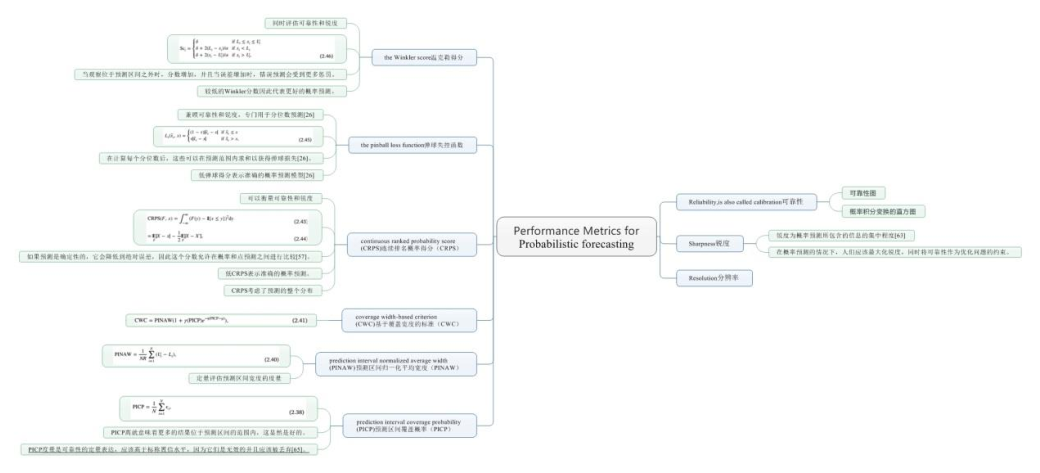
  与PIF和PLF相比，根据Hong等人的研究，概率风力预测（PWPF）是一个成熟的研究领域[13]，因此采用PWPF所需的性质似乎是合适的。Pinson等人[63]介绍了可靠性，清晰度和分辨率并将在此简要解释。

  可靠性，也称为校准[57]，是概率预测的重要质量，因为它表明观测的分布与预测的分布有多相似。如果由预测模型的分位数和观测模型的分位数产生的概率相同，则概率预测被认为是完全可靠的，并且与此的偏差将导致可靠性的降低[63]。它与预测的偏差有关，因为高可靠性对应于低偏差[26]。为了评估可靠性，构建了一个时间序列，用于监控模型超预测或欠预测的时间，之后可以绘制可靠性图。如果这个时间序列接近对角线，则说它具有高可靠性[63]。评估可靠性的另一种方法是评估概率积分变换（PIT）的直方图。根据定义，如果概率预测具有完美的可靠性，则PIT直方图是统一的[57]。

  可以设想锐度为概率预测所包含的信息的集中程度[63]。因此，高锐度是概率预测的基本特征，因为它降低了不确定性。事实上，Gneiting&&Katzfuss[57]提出，在概率预测的情况下，人们应该最大化锐度，同时将可靠性作为优化问题的约束。

  Pinson等人[63]已经确定了分辨率作为概率结果的可变性，取决于预测条件，也被称为Gneiting&&Katzfuss的分散[57]。Hong和Fan[26]提供了一个可理解的类比，他们指出，可以将分辨率与点预测中的预测方差进行比较。 在概率预测方面，人们希望零分辨率或色散，这意味着预测间隔的宽度保持不变。


  显然，概率预测的目的是确保观测的概率分布在预测区间内。为了评估是否是这种情况，可以计算预测区间覆盖概率（PICP） ，其公式如下[64]：

$$PICP=\frac{1}{N}\sum _{i=1}^N{ϵ}_i$$
这里${ϵ}_i$定义为：

$${ϵ}_i=\{\begin{array}{rcl}1& & if{x}_i\in [L_i,U_i]\\ 0& & if{x}_i\notin [L_i,U_i]\end{array}$$
  其中$L_i$和$U_i$分别代表预测区间的下限和上限。根据${ϵ}_i$的公式，我们可以推断出PICP高就意味着更多的结果位于预测区间的范围内，这显然是好的。PICP度量是可靠性的定量表达，应该高于标称置信水平，因为它们是无效的并且应该被丢弃[65]。

  然而，如果仅基于PICP分析预测的质量，则可以在下限Li和上限Ui之间选择宽范围，以便人为地改善覆盖概率，而预测的方差可以是不可取的，决策者提供的信息很少。事实上，预测区间的信息量由它们的宽度决定[64]。 因此，应该用预测区间归一化平均宽度 （PINAW）同时分析 PICP，这是一种定量评估预测区间宽度的度量。PINAW 定义如下[64]：

$$PINAW=\frac{1}{NR}\sum _{i=1}^N(U_i-L_i)$$
  其中R表示预测区间平均宽度的归一化，并表示最大预测值减去最小预测值。

  Khosravi等人[66]注意到PICP和PINAW通常具有直接关系，其中预测间隔（PINAW）的高宽度意味着结果的高覆盖率（PICP） ，因此提出了同时评估两者的定量测量。尽管作者将其命名为基于覆盖长度的标准(CLC)，但后来它被重命名为基于覆盖宽度的标准 （CWC） ，参见例如[64]。 CWC的表述如下[64]：

$$CWC=PINAW(1+\gamma (PICP)e^{-\eta (PICP-\mu )})$$
  其中η和μ是控制参数，训练期间 γ(PICP)=1。参数μ表示在训练阶段期间要实现的预分配的PICP，并且为了选择该参数，标称置信水平[(1−α)%]可以用作指导。此外，η是一个惩罚项，如果不满足预分配的 PICP，将导致CWC指数增长。当PICP≈μ时，人们已经实现了PICP和 PINAW之间的平衡，并且可以继续测试模型[64]。 然后，根据μ确定具有 γ(PICP)的CWC，其公式如下：

$$\gamma (PICP)=\{\begin{array}{rcl}0& & ifPICP\ge \mu \\ 1& & ifPICP<\mu \end{array}$$

  在测试阶段，使用式（2.42）比较CWC。如果PICP低于预先指定的PICP，则CWC增加。CWC的目标是在预测间隔[64]的信息量（PINAW）和覆盖概率（PICP）之间进行折衷，并且可以解释为信息和覆盖范围之间的最佳平衡。


  可靠性和锐度是概率预测的重要特性，但由于它们可以进行图形评估，因此对解释很敏感，这反过来可能导致主观结论，特别是在比较方法时[63]。因此，引入了要求适当的技能分数或评分规则，即确保最佳预测获得最高得分的分数。在下文中，将讨论三个度量，即连续排名概率得分（CRPS） ，弹球失控函数和温克勒得分。

  CRPS是一个强大的分数，其设计方式可以衡量可靠性和锐度。CRPS的一个优点是，如果预测是确定性的，它会降低到绝对误差，因此这个分数允许在概率和点预测之间进行比较[57]。CRPS可以如下表达[57]：

$$\begin{gathered} CRPS(F,x)={\int }_{-\infty }^{+\infty }(F(y)-1x<y{)}^{2}dy \\ =E_F|X-x|-\frac{1}{2}{E}_F|X-X^{{}^{\prime }}| \end{gathered}$$
  其中1是Heaviside 阶梯函数，x代表观测值，X和X’是具有累积分布函数(CDF)预测F和有限一阶矩[57]的独立随机变量。 CRPS的另一个优点是它具有与预测变量相同的单位[57]，这提高了分数的可解释性。此外，由于其与绝对误差的关系，低 CRPS 表示准确的概率预测。
  最后，从式（2.43）可以看出，CRPS考虑了预测的整个分布，这与将在下一段中讨论的弹球损失函数形成对比。

  与CRPS类似，弹球损失函数兼顾可靠性和锐度，专门用于分位数预测[26]，将在第3节中进行解释。定义如下[67]：

$$L_{\tau }({\tilde{x}}_{\tau },x)=\{\begin{array}{rclc}& (1-\tau )|{\tilde{x}}_{\tau }-x|& & if{\tilde{x}}_{\tau }\le x\\ & \tau |{\tilde{x}}_{\tau }-x|& & if{\tilde{x}}_{\tau }\ge x\end{array}$$
  其中${\tilde{x}}_{\tau }$是观测值x的分位数$\tau$的预测值。在计算每个分位数后， 这些可以在预测范围内求和以获得弹球损失[26]。值得注意的是，式（2.45）中定义的函数在分位数回归的情况下应最小化。低弹球得分表示准确的概率预测模型[26]。此外，在预测范围内平均所有分位数上的弹球损失会产生分位数分数[68]。

  Winkler评分[69]允许同时评估可靠性和锐度，类似于CRPS和弹球损失函数。令(1−α)为标称概率，则Winkler分数定义为[49]：

$$S{c}_i=\{\begin{array}{rclc}& \delta & & if{L}_i\le x_i\le U_i\\ & \delta +2(L_i-x_i)/\alpha & & if{x}_i<L_i\\ & \delta +2(x_i-U_i)/\alpha & & if{x}_i>U_i\end{array}$$
  其中$\delta =U_i-L_i$其中$L_i$和$U_i$表示前一天计算的预测区间的下限和上限。 从式（2.46）可以看出，当观察位于预测区间之外时，分数增加，并且当误差增加时，错误预测会受到更多惩罚。 此外，较低的Winkler分数因此代表更好的概率预测。为了评估整体表现，平均 Winkler评分可以定义为：
$$\overline{S{c}_i}=\frac{1}{N}\sum _{i=1}^{N}S{c}_i$$
  总结如下：

未完待续！

今天的文章光伏发电量和用电量的概率预测研究综述（1）分享到此就结束了，感谢您的阅读。