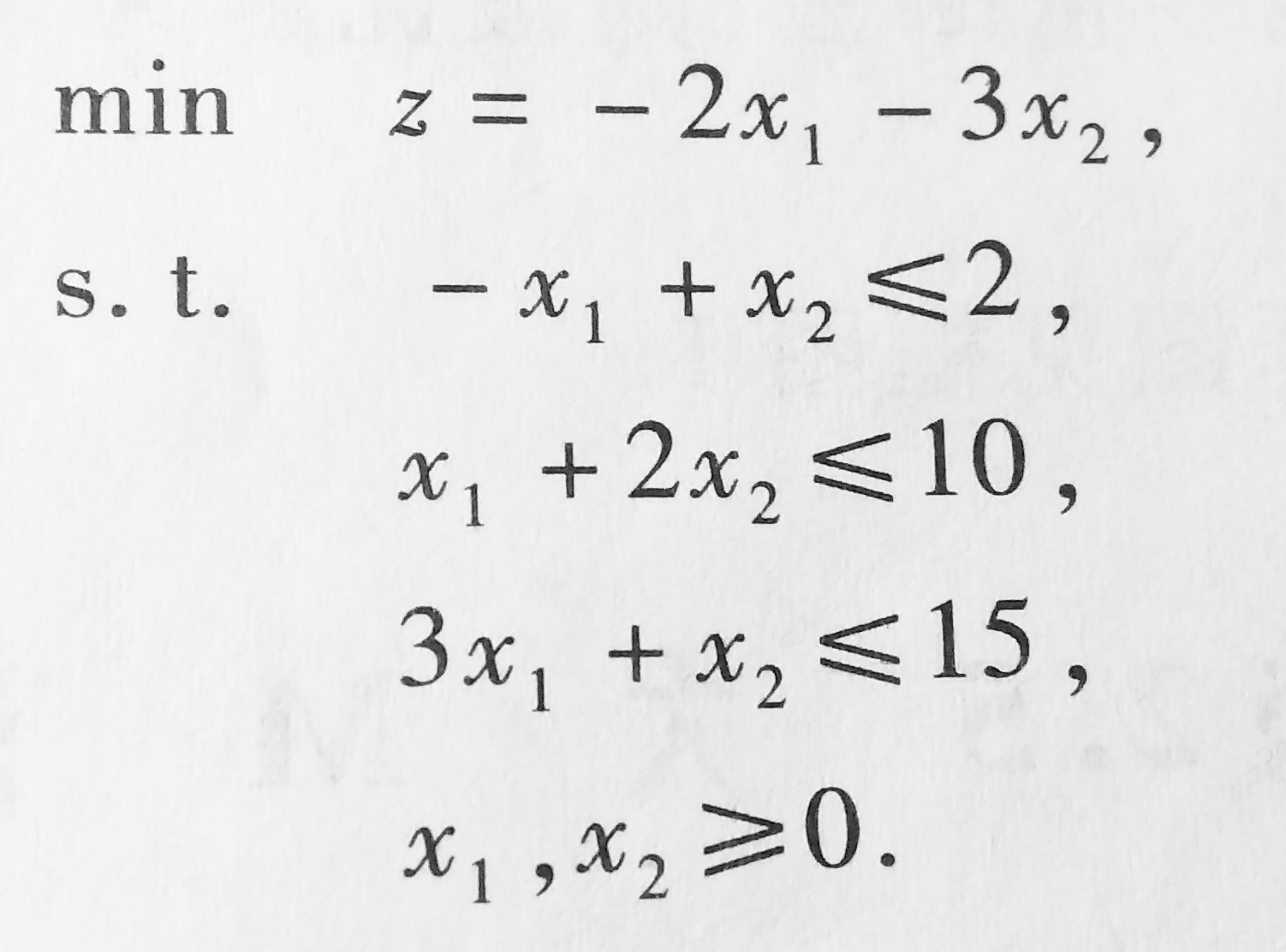MATLAB 实现单纯形法

对于形如
的代码实现

function [x,f,it]=linp(A,b,c) %输出x为最优解，f为最优值，it为迭代次数。
b=b(:);%变为列向量
it=0;
[m,n]=size(A);
x=zeros(1,n+length(b));
A=[A eye(length(b)) b]; %化为标准型，A b合一块
c=[c zeros(1,length(b)+1)]; %同上
 while ~all(c(1:length(c)-1)>=0) %并非所有的c中前length（c）-1个元素都大于等于零时进入循环
 d=find(c<0);%d(1)-------第一个负数元素列坐标
 e=find(A(:,d(1))>0);% e包含的d（1）列中正元素的行坐标
 g=[];
 for ii=1:length(e)
 g=[g A(e(ii),n+length(b)+1)/A(e(ii),d(1))];
 end
 h=find(g==min(g));%选择离基变量
 p=A(e(h),d(1));
 for ii=1:n+length(b)+1
 A(e(h),ii)=A(e(h),ii)/p;%离基变量 A(e(h),d(1)),对该行进行操作
 end
 j=-c(d(1))/A(e(h),d(1));
 for ii=1:n+length(b)+1
     c(ii)=j*A(e(h),ii)+c(ii);%%%%%对c操作
 end
 for ii=[1:e(h)-1,e(h)+1:m]
     j=-A(ii,d(1))/A(e(h),d(1));
     for kk=1:n+length(b)+1
     A(ii,kk)=j*A(e(h),kk)+A(ii,kk);
     end    
 end%%%%%%%%%%%%截止，对A的操作完成
 it=it+1;
 end
 o=[];
 for ii=1:n
     if all(A(:,ii)>=0)&&sum(A(:,ii))==1
     o=[o ii];
     end %x解的列坐标
 end
 for ii=1:length(o)
     for kk=1:m  %x解的行坐标
         if A(kk,o(ii))==1
             x(o(ii))=A(kk,n+length(b)+1); %对x解进行整理
         end
     end
 end  
 x=x(:);
 f=-c(n+length(b)+1);
end

测试：

>> A=[-1 1;1 2;3 1];
>> b=[2 10 15];
>> c=[-2 -3];
>> [x,f,it]=linp(A,b,c)

x =

     4
     3
     0
     0
     0


f =

   -17


it =

     2

>> 

结果正确

今天的文章MATLAB 实现单纯形法分享到此就结束了，感谢您的阅读。