Latent Variables的理解「建议收藏」

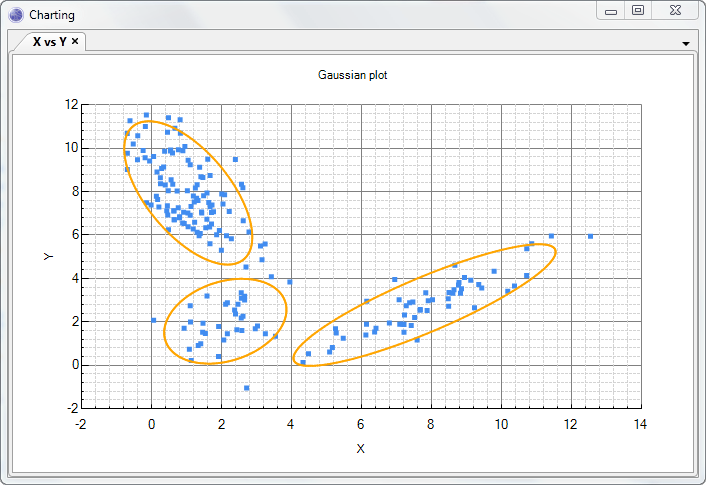
加入我们有X，Y两个随机变量，他们的概率分布如下。要直接用一个函数还表示这个分布是比较困难的。

但我们发现这个分布可以分成三个聚类。如果我们给每个聚类编号为。

那么就是简单的高斯函数了。

这里z就是

加入latent variable的意义在于，能够把复杂的问题变成多个简单的问题的和。

另外一种理解是，x是我们观察的值。这些观测值只是表面现象，但真正影响这些现象的是背后的一些latent variable。如果知道这些latent的取值，分布就会简单很多。这也是为什么概率inference里面也要研究latent variable。latent variable的问题，本身是个聚类的问题。也是找到系统的结构的问题。

比如在求的分布时，如果引入一个latent variable，就可以用EM进行迭代求解。

今天的文章Latent Variables的理解「建议收藏」分享到此就结束了，感谢您的阅读。