多目标优化 遗传算法_遗传算法的改进算法有哪些

遗传算法

        遗传算法在多目标优化问题处理中应用广泛，它的基本特征是通过在代与代之间维持由潜在解组成的种群来实现多向性和全局搜索，通过种群基于遗传的进化，实现潜在解向最终解的演变，这种种群到种群的方法在搜素Pareto解时是很有用的。

        遗传算法可以处理所有类型的目标函数和约束，不受制于他们的数学属性，可以在不考虑特定内部工作方式的前提下搜索解，因此在求解复杂问题解上比传统优化算法应用更多，可用性也更广。遗传算法作为启发式算法在处理单目标优化问题表现很好，后来逐渐的被引入多目标优化问题处理，现如今基于遗传算法的改进算法蓬勃发展，所以学习了解遗传算法是有必要的。

算法介绍

1. 算法结构

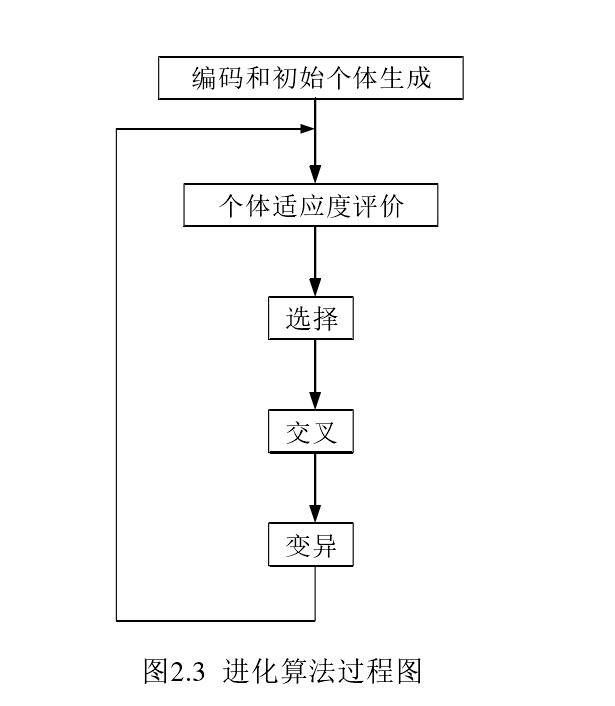
        算法过程如下：

        算法整体结构：

2. 结构分析

①初始种群的生成

       遗传算法是对种群进行操作的，初始种群的选择影响着算法的最终性能，所以初始种群的选择尤关重要。在处理实际问题时，问题的最优解在解空间的分布情况是不清楚的，所以设计初始种群时尽量设计成在解空间均匀分布（想法：参考自然界的进化规律，地球生物演化的起点是简单单细胞生物，是否可以以此参照设计初始种群，如从单个种群开始保持高突变率来演化成多种群，这样计算复杂度肯定高了但是否性能会变好？）。初始种群的个数是种群规模，依据问题复杂性，问题越复杂，目标空间维数越高，种群规模越大，反之亦然。常规的种群生成规则如下：

       有先验知识：利用先验知识在决策空间的生成均匀分布的初始种群。
       无先验知识：首先随机生成一定规模的初始种群，然后选取一部分适应度最好的，一小部分最差的，一小部分适中的个体，如此循环，直到种群规模满足要求。

②个体编码

       编码就是把实际问题变量转化成计算处理的决策空间变量，反之，把决策空间的解转成问题空间的解叫解码。编码的要求有三：

       （1）完备性：问题空间的任意解可以单射到决策空间。
       （2）健全性：决策空间的解可单射到问题空间的解。
       （3）非冗余性：问题空间的解和决策空间的解相互满射。

       编码的方法有多种，最有效最常用的是实数编码，其基因型空间中的拓扑结构与其表现型空间中的拓扑结构一致，因此很容易借鉴传统优化方法中的技术。根据实数编码，种群$P(t)$可以描述为：

       $P(t)=${
$x_{t,1},x_{t,2}\cdots x_{t,pop}$}
       $x_{t,j}=${
$(x_{t,j,1},$

今天的文章多目标优化 遗传算法_遗传算法的改进算法有哪些分享到此就结束了，感谢您的阅读。